基于扩展多面体组合单元的非规则颗粒材料离散元方法

李典哲, 刘 璐, 季顺迎

(大连理工大学 工业装备结构分析国家重点实验室, 辽宁 大连 116024)

0 引 言

离散单元法(discrete element method)能全面反应颗粒材料的宏微观力学特性,是预测颗粒材料力学行为的有效工具[1-3]．由于球形颗粒具有易于构造、接触判断简单等优点,常被用于离散元数值模拟[4-8]．然而,自然界与工业生产中的碎砾石、泥沙和道砟等真实颗粒的形态往往都是非规则的、复杂的[9-10]．颗粒形状对颗粒系统的动力学行为影响很大[11-14]．与球形颗粒相比,非规则颗粒表面不平整、不连续,其流动状态也呈间歇性流动[15]．由于非规则颗粒之间容易形成互锁效应,阻碍颗粒的相对运动,其往往具有较大的空隙率和较小的流动速度[16]．同时,在颗粒堆积过程中,非规则颗粒的体积分数较小而休止角较大[17]．从球形颗粒系统中得到的结论难以直接、准确地应用到非规则颗粒系统上．因此,在离散元数值模拟中发展非规则颗粒的理论模型是十分必要的．

为能更准确地模拟真实颗粒系统,各种非规则颗粒的构建方法不断被提出．由二次曲面函数可构造得到椭球体单元,并且通过调整参数可得到二维圆盘、三维细长或扁平椭球体等不同形状颗粒[18-19]．超二次曲面单元是椭球体单元的扩展,通过超二次曲面函数可构造出几何对称的颗粒单元,改变函数参数可获得具有不同表面尖锐度和长宽比的圆柱体、椭球体等颗粒单元[20-22]．多面体单元是基于拓扑结构的颗粒单元,可表示尖锐的角点和棱边,能很好地反映出自然界中颗粒材料的真实形态[23-24]．与多面体单元相比,扩展多面体单元是基于Minkowski和定义由任意多面体和扩展球体构建而成的,通过改变扩展半径可得到具有不同表面尖锐度的颗粒单元[25-26]．其避免了纯多面体难以直接通过几何元素判断接触的缺点,提高了接触搜索效率[27]．然而,这些颗粒模型只适用于构造凸形颗粒．近年来,针对凹形颗粒的离散元方法也在不断发展．Li等用凹形函数确定心形颗粒形态,再通过网格法来确定颗粒之间的接触点,其计算效率随形状函数复杂度的增加而降低[28]．王嗣强等采用球谐函数描述了任意几何颗粒形态,运用基于水平集方法的任意形态接触算法确定了颗粒间的接触方向和重叠量[29]．Feng将任意颗粒形态离散成一系列三角单元,通过能量守恒接触模型确定颗粒之间的接触力、接触法向[30-31]．尽管上述构造方法均能有效描述任意形态的颗粒单元,但由于接触计算的复杂性,导致离散元数值模拟时间大大增加．

为描述任意形态颗粒材料的几何构型,组合单元法被提出且不断完善发展[32]．组合单元法可组合不同数目的任意基本单元,且允许颗粒之间重叠,进而构造出不同形态的颗粒．组合方法的优势在于其接触判断可简化为一系列简单的基本颗粒之间的接触判断[33]．组合单元一直在不断地完善与发展,其组成基本颗粒包括球体、椭球体、圆柱体和超二次曲面等．组合球体单元通过将一定数量的球体颗粒组合起来,构造出形状复杂的非规则颗粒,因球体单元易于构造、接触判断简单等优点而最先发展并广泛应用[34-35]．组合椭球体单元基于二次曲面函数,将若干个椭球体颗粒组合而成[36]．与椭球体相比,组合单元更好地描述了颗粒形状的不对称性,更加接近真实颗粒形态．组合超二次曲面单元基于超二次曲面方程,将多个超二次曲面单元进行任意组合,且基本单元之间存在重叠量,可用于构造任意形态颗粒材料[37]．

本文通过组合扩展多面体单元构造了形态各异的颗粒材料．采用背景网格法计算该模型的质量和转动惯量,消除了颗粒间重叠带来的影响．将组合颗粒的接触判断转化为其基本颗粒之间的接触判断．通过不同形态组合颗粒的堆积与卸料过程的离散元模拟,验证了该方法的可行性．

1 基于扩展多面体组合单元的模型

基于组合离散元方法构建扩展多面体组合单元,采用背景网格法计算组合单元的质量特性,并将组合单元间的接触问题简化为其基本单元间接触判断,最后对组合单元的平动与转动进行求解．

1.1 基于Minkowski和的扩展多面体单元

Minkowski和理论最早由德国数学家Herman Minkowski提出,其在Euclid几何空间中给定了两个空间体A和B,将两个空间点集相叠加得到新的空间体集合,其表达式为[38]

A⊕B={x+y|x∈A,y∈B},

(1)

式中,x和y分别为空间体A和B对应的空间坐标．

依据Minkowski和的定义,将A和B两个空间体设置为任意多面体和扩展球体,构建得到扩展多面体单元[39]．通过改变球体的扩展半径可构建具有不同粒子尖锐度的扩展多面体单元,如图1所示．

图1 由不同扩展半径球体与多面体构造的扩展多面体单元Fig. 1 Dilated polyhedrons composed of various dilated spheres and polyhedrons

1.2 扩展多面体组合单元的构造

以往离散元方法主要集中在构造凸形颗粒单元[40-42]．为更准确地构建形状更为复杂的凹形颗粒,本文基于组合离散元方法将多个不同形态的扩展多面体单元组合起来,且颗粒之间可存在一定重叠量,进而构造任意形态的颗粒材料．不同颗粒形态的扩展多面体组合单元如图2所示．

图2 不同形态的扩展多面体组合单元Fig. 2 Multi-dilated polyhedron elements with various shapes

1.3 扩展多面体组合单元计算参数的确定

考虑组合单元由可重叠的任意扩展多面体颗粒组成,且基本颗粒单元之间可存在较大的重叠量．颗粒之间的重叠会导致质量特性的重复计算,不宜准确得到组合单元的运动信息．为此,本文采用背景网格法计算组合单元的质量、质心和转动惯量,以避免重复计算带来的影响[37],如图3所示．

图3 基于背景网格法的组合单元质量和惯性矩计算Fig. 3 Calculation of the mass and the moment of inertia for multi-dilated polyhedrons

通过组合单元所在空间位置确定网格的计算区域,并沿计算区域的3个方向进行划分,由此得到多个微单元．空间网格越多,微单元越小,计算精度越高．根据每个微单元网格质心是否在组合单元内来判断有效微单元网格的数量,通过叠加有效微单元网格的质量得到组合单元质量,其表达式为

(2)

式中,m为组合单元质量;ρ为密度;Nx,Ny和Nz分别为x,y和z方向上有效微单元网格的数量;lnx,lny和lnz分别为微单元在x,y和z方向上的边长．

组合单元的质心可写作

(3)

(4)

(5)

式中,Cx,Cy和Cz分别为组合单元质心在x,y和z方向上的坐标位置;xg,yg和zg分别为微单元网格在x,y和z方向上的中心坐标位置．

组合单元的惯性张量可写作

(6)

(7)

(8)

(9)

(10)

(11)

1.4 组合单元的接触判断

接触判断是离散元数值模拟的一个重要环节,对计算效率有很大的影响．这里采用二阶多面体扩展函数与球面函数加权求和的方法得到扩展多面体的包络函数, 从而将扩展多面体间的接触问题转化为两个包络函数之间的优化问题．通过求解优化问题快速确定颗粒间的接触法向和重叠量,有效地提高了扩展多面体单元的接触搜索效率[43]．该包络函数的归一化形式为

(12)

式中,k为颗粒光滑度系数,R为球面函数的半径．

优化模型的表达式为：

(13)

式中,fA和fB分别为两个基本单元的包络函数．

由包络函数构造的扩展多面体颗粒需要满足严格凸形的条件[44],而扩展多面体组合单元形态往往是不规则的、凹形的．但事实上,已证明了两个组合单元之间的接触重叠,至少存在一对基本单元相互接触[33]．因此,两个组合单元之间的接触问题可转化为其基本单元即扩展多面体颗粒之间的接触问题．组合单元可采用与扩展多面体颗粒相同的接触判断方法．图4为两个相互接触的组合单元．

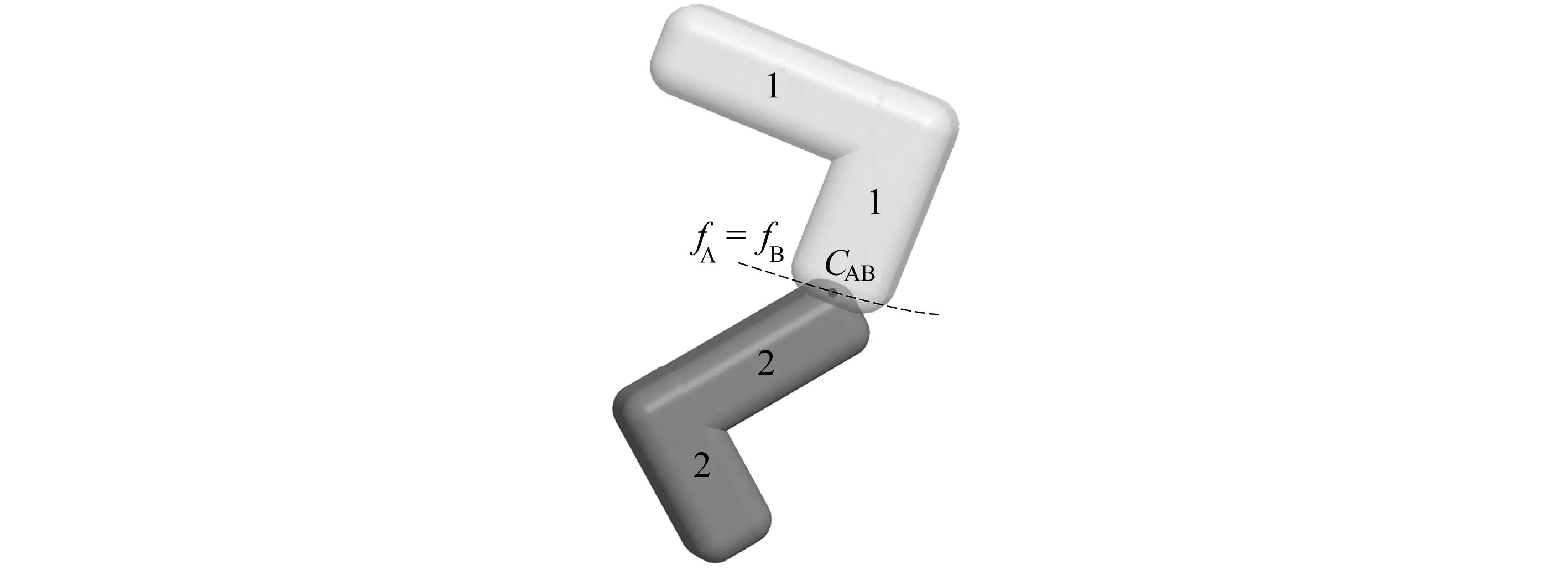
图4 扩展多面体组合单元间的接触判断Fig. 4 The contact detection between multi-dilated polyhedrons

1.5 扩展多面体组合单元的运动

1.5.1 组合单元合力、合力矩计算

组合单元的运动可分为平动和转动两部分,根据Newton第二定律列出其运动方程如下：

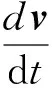
(14)

(15)

式中,m,I分别为组合单元的质量和惯性张量;dv/dt,dω/dt分别为组合单元的加速度和角加速度;∑F,∑M分别为组合单元的合力和合力矩;g为重力加速度．

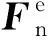
(16)

(17)

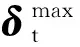
对于组合单元来说,合力∑F和合力矩∑M的计算是将所有基本单元的接触力、接触力矩进行叠加．将作用在基本单元上的接触力相对于组合单元质心进行累加．

1.5.2 组合单元的平动与转动

组合单元所在空间坐标系可分为整体坐标系(G)和以组合单元质心为原点的全局坐标系(GL)和局部坐标系(B)．组合单元平动时,局部坐标系(B)随之发生平动,其动力学方程可写作

ak+1=Fk+1/m,

(18)

(19)

(20)

式中,F,a和v分别为组合单元的合力、加速度和速度;x为组合单元的位置信息;k,k+1分别表示当前时刻和下一时刻,其间隔用Δt表示．

组合单元是一个刚体,所有基本单元与组合单元之间的相对位置都是恒定的．因此,通过更新组合单元的坐标位置与所有基本单元和组合单元的相对位置,就可以得到所有基本单元的位置信息,可表示为

(21)

式中,i为基本单元的编号,xi为下一时刻第i个基本单元位置信息;Δxi为第i个基本单元与其组合单元质心的相对位置．

组合单元转动时其运动可视为局部坐标系(B)在全局坐标系(GL)下的运动．局部坐标系下的坐标eB与全局坐标系下的坐标eGL,其转换关系可表示为

eB=R·eGL,

(22)

式中,R为转换矩阵,可由四元数q(q0,q1,q2,q3)求得,其可写作

(23)

作用在组合单元上的合力矩M在局部坐标系下可表示为MB=R·M．根据组合单元转动的动力学方程可求得下一时刻局部坐标系下组合单元的角速度,即

(24)

(25)

(26)

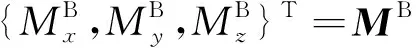
由式(24)—(26)求得下一时刻局部坐标系下组合单元转速,然后再对组合单元四元数进行更新,即

(27)

随后,将更新后的四元数再次代入方程 (23)中,计算得到下一时刻的转换矩阵．通过更新后的转化矩阵将局部坐标系下组合单元的角速度转化为全局坐标系下的转速．

2 扩展多面体组合单元运动过程的离散元分析

通过与已有文献的结果对比了两类组合单元的卸料过程,验证了该模型的有效性．其次,模拟不同形态单元的堆积、卸料过程,并分析颗粒形状对体积分数、卸料流量和配位角的影响．

2.1 颗粒材料在平底漏斗中卸料过程的离散元分析

为验证扩展多面体组合单元的有效性,并与已有文献结果进行对比[46]．本文选取了文献[46]中的两类单元,分别模拟其在长方形平底漏斗中的卸料过程．图5中的这两类单元分别是由一个基本颗粒构成的凸形三棱柱单元和由两个基本颗粒构成的凹形正倒锥体单元,其可看作是在凸形三棱柱单元基础上将其两个矩形面旋转45°得到．

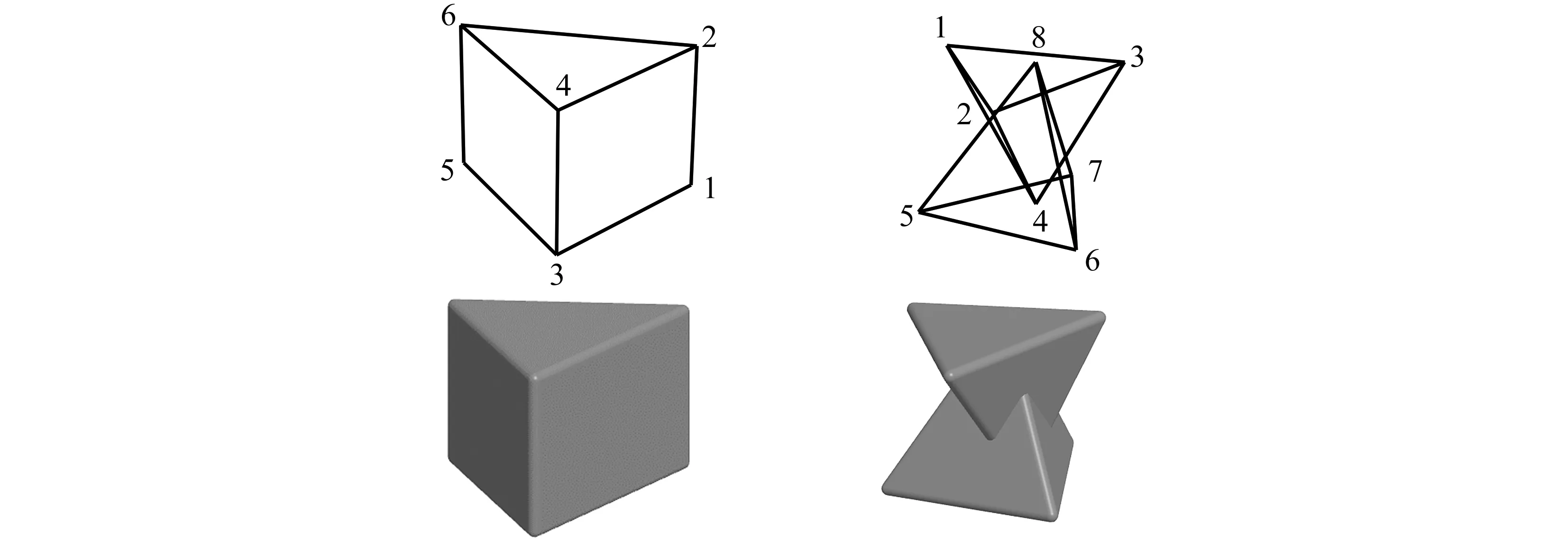
图5 凸形三棱柱单元和凹形正倒锥体单元Fig. 5 The convex triangular prism element and the concave upward-downward conical element

长方形平底漏斗几何形状如图6所示,其长、宽、高分别为0.14 m,0.05 m和0.4 m,漏斗挡板尺寸为0.04 m×0.05 m．这里选取600个蓝色颗粒和400个红色颗粒,并将其划分为5层,以便更好地观察颗粒的堆积和卸料过程．表1给出了数值模拟中的主要计算参数,包括颗粒的特定参数和一般模拟参数[46]．初始时漏斗中放置挡板,所有颗粒具有随机位置和空间方位,在重力作用下自由下落堆积．当颗粒堆积稳定后撤去挡板,完成漏斗卸料过程．

表1 两种扩展多面体组合单元的主要计算参数

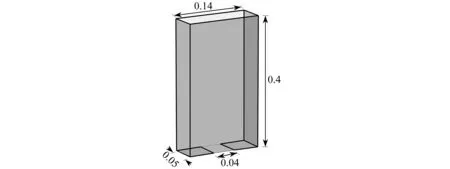
图6 平底漏斗几何形状(单位： m)Fig. 6 The geometry shape of the flat bottom hopper (unit： m)

将两种组合单元模拟平底卸料过程所得结果与相关试验以及离散元模拟结果[46]进行比较分析,如图7、图8所示．在三棱柱单元的模拟中,组合单元的流动从中间向边缘发展,组合单元逐渐呈V型流动．这主要是由于漏斗中心的颗粒速度要高于两侧边壁的颗粒速度．已有的试验和模拟中分别在1.6 s和2.4 s时形成准稳定拱门,但在大多数情况下这些准稳定拱门最终会坍塌[46]．而在本文的模拟中,首先在1.6 s处观察到准稳定拱门的形成,而后拱门坍塌,漏斗继续卸料,2.4 s时再次形成准稳定拱门．这主要是因为凸形颗粒的流动是连续的,也更容易滑动和转动,不能像凹形颗粒一样互锁形成稳定的拱形结构．而对于凹形正倒锥体单元,在已有的试验、模拟以及本文的数值模拟中均在0.8s处形成稳定的拱形结构,且在整个模拟过程中拱形结构保持稳定．这主要是因为凹形颗粒之间的互锁结构阻碍了组合颗粒的连续流动．其次,靠近边壁的凹形颗粒更容易形成互锁效应,从而形成更为稳定的拱形结构．

图7 凸形三棱柱单元卸料过程的离散元模拟与试验对比Fig. 7 The convex triangular prism element’s discharge process simulated with the DEM and compared with the physical experimental results

为进一步验证本文离散元方法的可靠性,下面将卸料过程的流量进行对比分析．文献[46]共进行了20次试验和5次数值模拟,其中20次试验的结果存在一定差异,这主要是由于颗粒材料的初始排列状态具有很强的随机分布规律,导致最终堆积状态不同,这会对卸料结果产生一定影响[46]．图9为平底漏斗卸料过程中剩余颗粒比例随时间的变化情况,在此给出了文献[46]20次试验结果的上下限和一次数值模拟的结果．可以看到,对于凸形三棱柱单元,本文模拟结果在文献[46]试验结果的区域范围内,且与离散元模拟结果在趋势上是一致的．此外,本文模拟结果与文献[46]的模拟结果最终剩余颗粒比例相近,不同的是开始时本文模拟漏斗卸料速度更快．这主要是因为在本次模拟中我们选择的基本单元为扩展多面体单元,即使给定的扩展半径很小,但其较多面体而言,颗粒表面更为光滑,颗粒也更易流动．

对于凹形正倒锥体单元,本文模拟所得结果与文献[46]的试验、离散元模拟结果在趋势上一致,且其位于试验结果的区域范围内．显然,在最终稳定状态下平底漏斗中剩余颗粒比例与已有试验结果上限相近．从整体上看,本文模拟结果与文献[46]的试验和离散元模拟结果是一致的．

2.2 颗粒材料堆积过程的离散元模拟

通过组合扩展多面体颗粒构造6种不同形态的组合单元,如图10所示,其中L,W和H分别表示颗粒的长、宽和高,这里取L=100 mm,W=30 mm,H=180 mm．采用4 000个颗粒材料进行堆积过程的离散元模拟,其主要计算参数列于表2中．

图10 不同形态的扩展多面体组合单元Fig. 10 Multi-dilated polyhedrons with various shapes

长方体容器的长、宽和高分别为L0=1.8 m,W0=1.8 m和H0=5.0 m．初始时刻,所有组合单元具有随机位置和空间方位,且组合单元之间无重叠,在重力作用下下落堆积．下落一段时间后,组合单元保持静止,形成稳定的颗粒床,如图11所示,其中颗粒颜色表示其距离底部的距离．颗粒形状对堆积分数的影响如图12所示．不同颗粒之间堆积密度大不相同,其中O形颗粒较其他颗粒具有更高的堆积密度和更低的孔隙率．这主要是由于O形构造使得其空心部分位于颗粒中间,难以与其他颗粒勾结互锁,颗粒更容易发生相对滑动和转动．其次,T形、Z形和K形相比于A形和C形有更高的堆积密度和更低的孔隙率．这主要是由于A形、C形相较于T形、Z形和K形的空心部分更大,其更容易与多个颗粒产生显著的互锁效应,使得颗粒之间难以发生相对运动．由此可见,颗粒形状对颗粒床的堆积密度有显著影响,且随颗粒形状复杂度的增加,颗粒的体积分数不断降低．

图11 扩展多面体组合单元形成的稳定颗粒床Fig. 11 Stable granular beds composed of multi-dilated polyhedrons

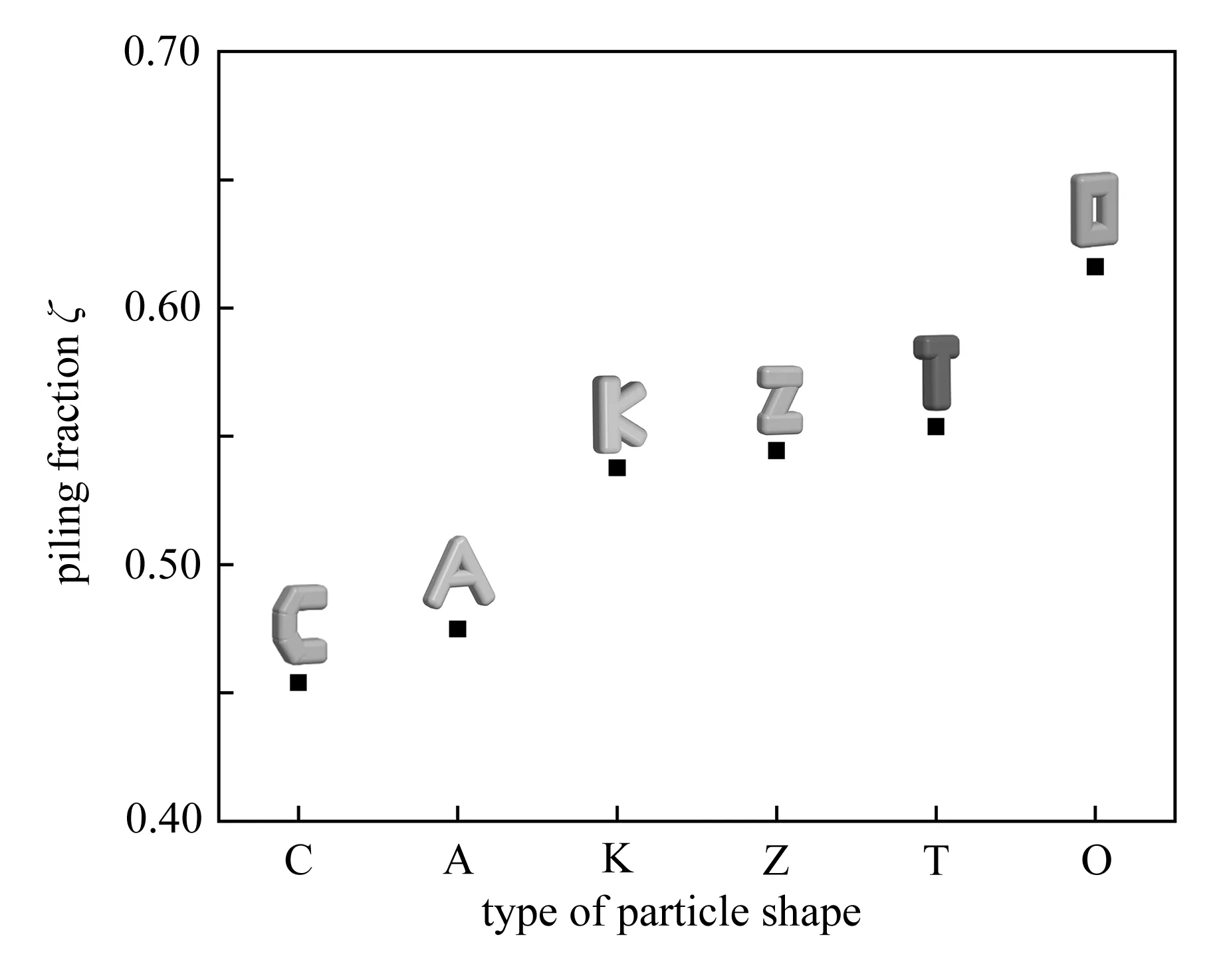
图12 颗粒形状对堆积分数的影响Fig. 12 Effects of particle shapes on the piling fraction

2.3 颗粒材料卸料过程的离散元模拟

通过不同扩展多面体颗粒可构造形态各异的组合单元,其颗粒形态将影响流动行为．这里采用扩展多面体的不同组合形式构造4种组合单元,组合单元总数为4 000,其长、宽和高均相同,分别为L=1 m,W=1 m,H=1 m．初始时刻,组合颗粒在上部漏斗中进行堆积,形成稳定床后,采用3种颜色按照高度对颗粒床均匀地划分为3层(蓝色、绿色和红色)．颗粒床堆积稳定后,将上部漏斗的孔口打开,颗粒开始卸料．图13显示了不同时刻颗粒的卸料过程．颗粒尺寸较大且凹形颗粒之间易形成互锁结构阻碍颗粒流动,因此,将上部漏斗的孔口尺寸设置偏大,L1=W1=8 m．其中,L0∶W0∶H0=2∶2∶1,如图14所示．漏斗孔口打开后底层蓝色颗粒全部流出,颗粒逐渐呈V型流动,这主要是由于漏斗中心的颗粒速度高于靠近边壁的颗粒速度．凹形颗粒之间易形成互锁结构,颗粒不易滑动和滚动,因此在卸料结束后颗粒出现明显的分层图案．

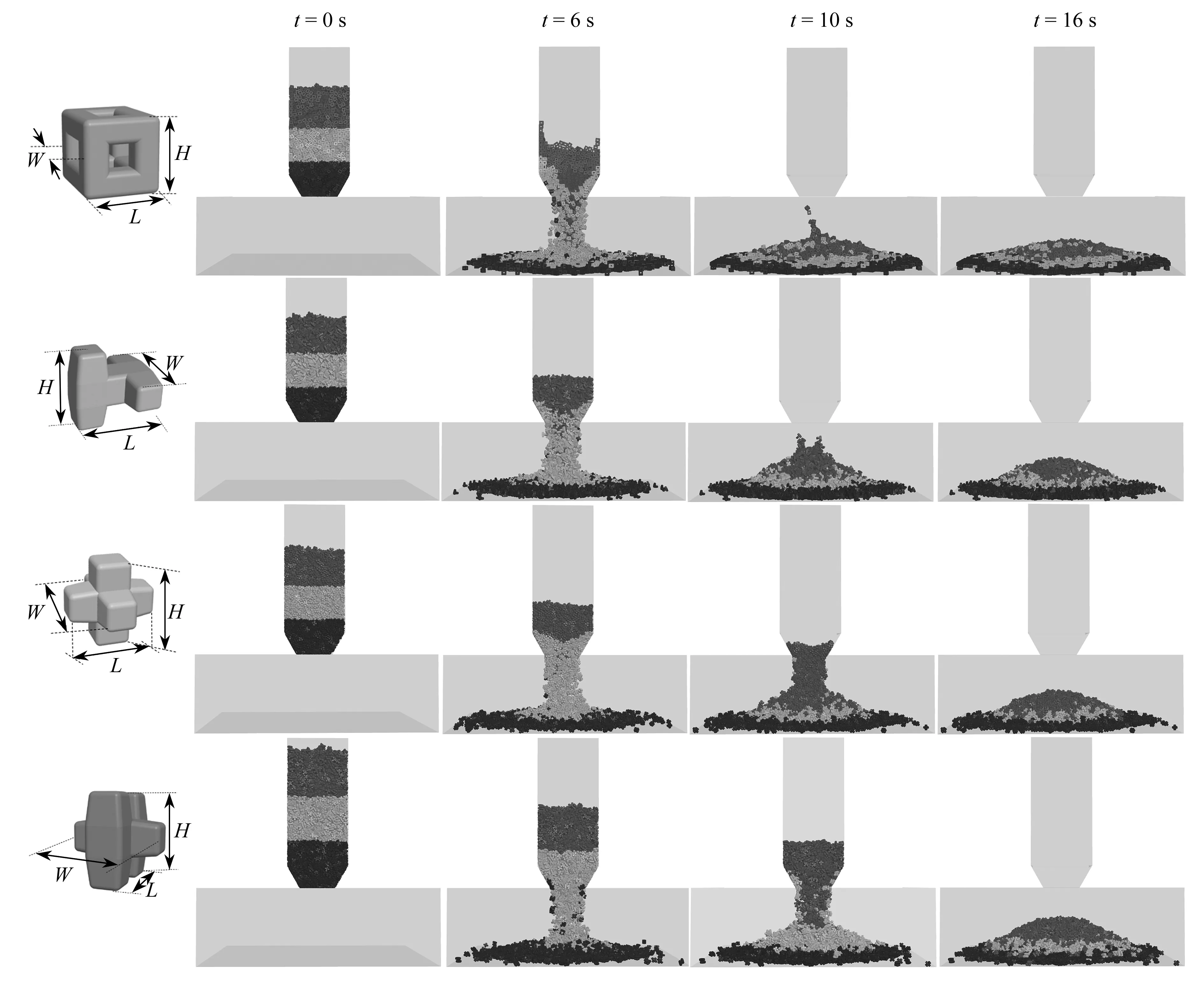
图13 不同时刻下组合单元的卸料过程Fig. 13 Discharging processes of multi-dilated polyhedrons at different moments

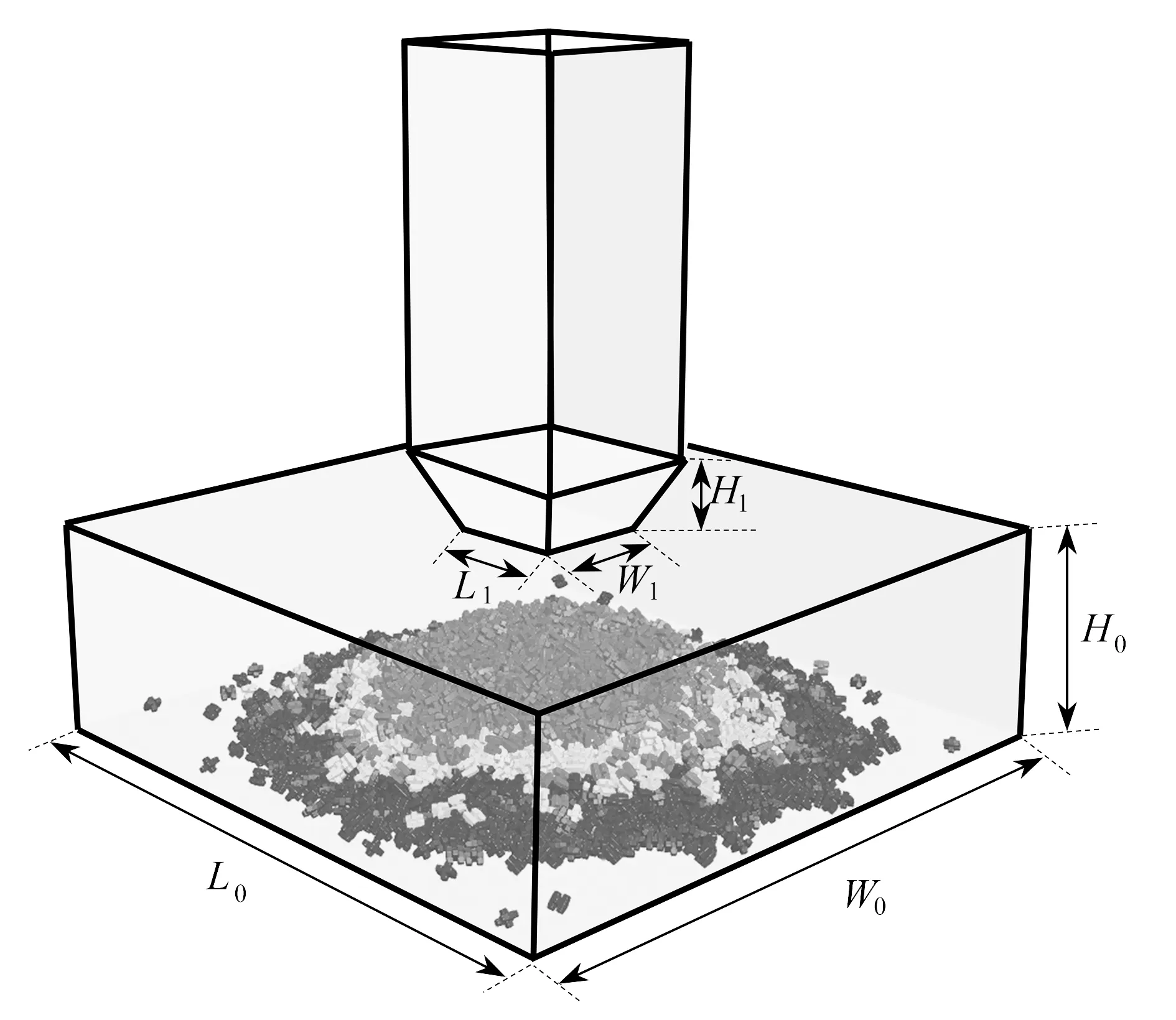
图14 卸料漏斗的几何尺寸Fig. 14 The geometry shape of the hopper model

不同颗粒形状所对应的卸料流量和休止角影响如图15所示．在卸料过程中,空心体组合单元具有最快的流动速率且最先完成卸料过程,而扭王字组合单元具有最慢的流动速率．卸料完成后,组合单元在漏斗底部保持静止,形成稳定的堆积床．其中,空心体组合单元具有最小的休止角,而扭王字组合单元具有最大的休止角．这主要是因为颗粒材料形状的复杂度显著影响颗粒的堆积和卸料过程,凹形颗粒形状越复杂,颗粒之间的互锁效应越明显,颗粒之间越不容易滑动和相对转动．

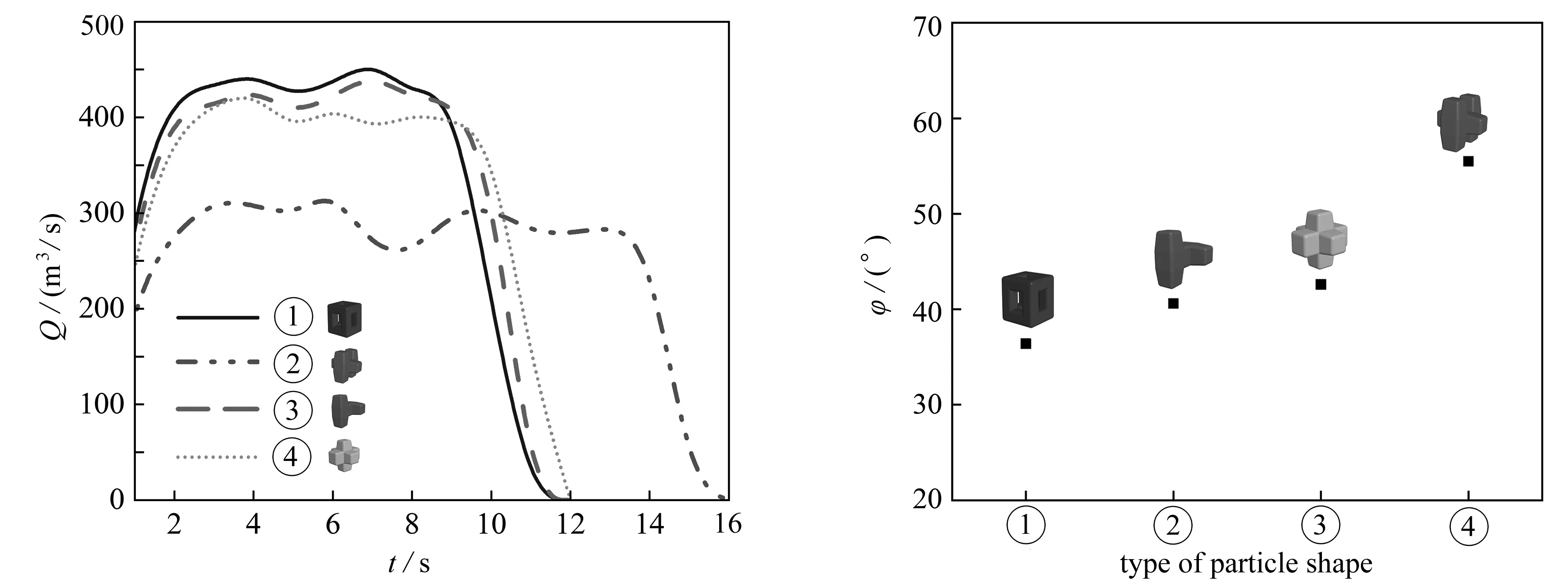
(a) 卸料流量 (b) 休止角(a) The mass flow rate (b) The angle of repose

3 结 论

本文以Minkowski和方法构造的扩展多面体颗粒为基本单元,基于组合单元方法提出了一种任意形态扩展多面体组合模型．为验证该模型的准确性,分别模拟了凸形三棱柱单元、凹形正倒锥体单元在平底漏斗中的卸料过程,并与已有试验结果进行了对比验证．基于组合方法构造了形状各异的颗粒材料,并进行了试验验证,包括下落堆积和动态漏斗卸料．此外,本文还研究了颗粒形状对堆积密度、卸料流量和休止角的影响．计算结果表明,组合单元形状的复杂度显著影响颗粒材料的堆积与卸料,并且随着组合单元形状复杂度的增加,颗粒的堆积密度与流动速率随之降低,而休止角随之增加．组合单元模型的有效应用,为任意形态颗粒材料的离散元数值模拟提供了一种新思路．