Gauss白噪声激励下的永磁同步电动机模型的分岔分析

叶正伟, 邓生文, 梁相玲

(1. 广东科技学院 通识教育学院, 广东 东莞 523000;2. 广东理工学院 基础课教学研究部, 广东 肇庆 526100;3. 喀什大学 数学与统计学院, 新疆 喀什 844000)

0 引 言

永磁同步电机(PMSM)是一种新型电机,具有高功率密度、大转矩惯性比、小体积等特点,广泛应用于船舶、航天、新能源汽车等领域．其模型作为典型的非线性系统,最早由Hemati等[1-2]于20世纪90年代提出,后经发展逐渐完善．我国学者对其及相关转子系统进行了深入的研究．文献[3]运用非线性动力学理论和方法分析了永磁同步电机系统在特定参数变化下的混沌和分岔．文献[4]以永磁同步电机的数学模型为基础,根据中心流形定理进行降维简化处理,讨论了永磁同步电机模型的Hopf分岔问题．唐传胜等[5]提出了一种考虑不确定参数混沌系统的改进控制器,并进行了数值仿真,模拟结果表明改进的控制器有更强的鲁棒性．文献[6]通过Lyapunov指数图、Poincare截面、相轨迹,研究了各种参数变化下系统的分岔及混沌控制．文献[7-8]基于GPU计算,探究了多参数变化下的旋转机械系统的动力学行为,发现了一些有趣的分岔结构．永磁同步电机模型是一个典型的强非线性动力系统模型,大量的研究工作是基于确定的理论展开的,除了确定的永磁同步电机系统的非线性动力学分析外,一些文献在永磁同步电动机模型中引入扰动项．文献[9]运用非线性动力学理论分析了正弦扰动项下非均匀气隙的永磁同步电机模型的稳定性．文献[10]利用根据包映射有向图法分析了噪声干扰下永磁同步风力发电机的随机分岔,通过数值模拟得到了整体结构的演化规律．

许多研究表明,任何动力系统都无法避免外界干扰,而普遍存在的随机噪声会对系统产生双重影响：一方面,随机噪声可以促进系统进入理想状态,如随机共振[11-13]、神经元脉冲放电和网络同步;另一方面,噪声会干扰动态系统的周期振荡行为,引起混沌．在实际应用中,这种影响广泛存在于生物工程、机械工程等多领域．文献[14]研究了Markov状态切换和白噪声扰动下的一类具有Gilpin-Ayala增长的随机捕食-食饵模型的动力学行为,得到了系统随机持久和灭绝的阈值,并根据数值模拟验证了结论的有效性．文献[15]对网络传染病模型引入白噪声,通过随机动力系统理论,得到了随机灭绝和持久的条件,由数值模拟验证了理论结果．文献[16-17]通过随机动力学理论介绍了随机噪声激励下调速器系统的随机稳定性,并由数值模拟,探究了系统在双参数空间中的复杂动力学行为．文献[18]建立了色噪声激励下的水轮机调节系统,探究了系统的随机分岔,并通过数值模拟验证．文献[19]讨论了眼动系统在Gauss白噪声激励下的随机分岔,噪声强度和抑制性神经元的作用强度都能诱导产生随机P分岔现象．在实际工作中,永磁同步电动机系统也不可避免地受到外部环境和内部传动系统的影响,例如温度起伏、磁场变换[20]、阻尼改变等．这些影响因素可能会对内部机理起到消极作用,将这些影响因素视作随机噪声更接近实际情况[21]．由此,本文建立了Gauss白噪声激励的永磁同步电动机模型,进行了随机噪声激励下的分岔分析,从而为其平稳运行增加鲁棒性提供了理论意义．

本文的主要结构如下：第1节将Gauss白噪声引入永磁同步电机系统,通过极坐标变换和随机平均法得到It随机微分方程;在第2节中,通过计算推导得到了系统概率密度函数,并进行了数值模拟,随着噪声强度的增加,系统在概率密度函数的演化过程中出现P-分岔;第3节在双参数空间中探究了引入噪声前后系统的复杂动力学特性;第4节总结了噪声对永磁同步电动机系统的影响,其结果有助于研究该电机系统的平稳运行．

1 模 型 处 理

以电流id,iq及转子角速度ω为变量的永磁同步电动机模型为

(1)

其中,参数Ld,Lq表示d-q轴电感;R1为定子绕组;TL为负载转矩;ψr为永磁磁通;β为阻尼系数;P为极对数;J为转动惯量;ud,uq表示定子d-q轴电压．

考虑一般情形,交直轴电感近似相等Ld=Lq=L,此时模型(1)进一步变为

(1)′

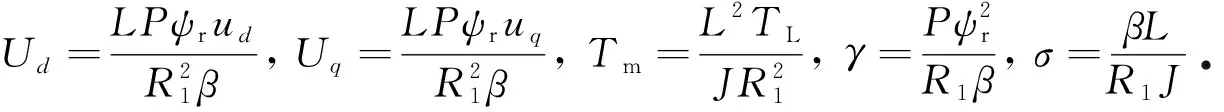
考虑系统(1)′容易受随机因素影响变得不稳定,对其引入Gauss白噪声ξ(t)得到随机微分方程为

(2)

(3)

令

其中

方程(3)可化为

(4)

其中

M=M21M32-M22M31,N=M21M32-M22M31-M23M32．

此时系统具有局部不变流行：

可对方程(4)降维得

(5)

ζ的全微分方程为dζ/dt=∂hφ·dφ/dt+∂hη·dη/dt．

接下来,我们可以得到

-(a+ε)h+c1φ2+c2φη+c3φh+c4η2+c5ηh+Dhξ(t),

(6)

且h(φ,η)的逼近式为

h(φ,η)=h1φ2+h2φη+h3φDξ(t)+h4η2+h5ηDξ(t)+…．

(7)

一定的误差范围内,系统(5)可变为

(8)

令φ=rcosθ,η=rsinθ, 经过极坐标变换,系统(8)可变为

(9)

其中

f1(r,θ,ξ(t))=a1r2cos3θ+b4r2sin3θ+(a2+b1)r2cos2θsinθ+a3h1r3cos4θ+

(a3h2+a5h1)r3cos3θsinθ+(a3h4+a5h2+b3h2+b5h1)r3cos2θsin2θ+

(a5h4+b3h4+b5h2)r3cosθsin3θ+(b2+a4)r2cosθsin2θ+

b3h1r3cos3θsinθ+b5h4r3sin4θ+Drcosθ·ξ(t),

b3h2r2cos3θsinθ+(b3h4+b5h2-a3h2-a5h1)r2cos2θsin2θ+

(b4-a2)rcosθsin2θ+(b5h1-a3h1)r2+(b5h1-a3h1)r2cos3θsinθ+

cos3θsinθ+(b5h4-a3h4-a5h2)r2cosθsin3θ-a5h4r2sin4θ+Drsinθ·ξ(t)．

已知反应{r(t),θ(t)}弱收敛于二维Markov过程,根据随机平均法,方程(9)的It微分方程如下：

(10)

其中w(t)为标准Wiener过程[22],dt和dw分别为漂移系数和扩散系数,且

v1=8D2,v2=3a3h1+a3h4+a5h2+b3h2+b5h1+3b5h4,v3=8D2,

v4=3b3h1+b3h4+b5h2-a3h2-a5h1-3a5h4,v5=D2/2．

基于扩散矩阵,可得到一维的Markov过程的平均振幅r(t)：

(11)

2 P-分岔

当平稳概率密度的性态发生变化时,系统将会发生P-分岔,所以我们通过平稳概率密度函数研究P-分岔．根据It微分方程(11),得到相应的FPK方程如下：

(12)

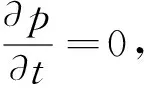
(13)

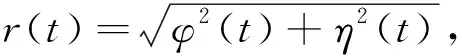
(14)

设置一组参数：

Ld=Lq=L=12 mH,R1=0.84 Ω,ψr=0.8 Wb,P=3,J=10-5kg·m2,

β=0.017 5 N·m·s,TL=0.25 N·m,ud=13.2 V,uq=45 V．

讨论噪声强度D对系统分岔的影响,其仿真图像见图1．

图1 随噪声强度D变化的联合概率密度图及其俯视图Fig. 1 The joint probability density function with the change of noise intensity D

从图1(a)可以看出,当噪声强度D=0.1时,联合概率密度函数为单峰形状,函数p(φ,η)的最高点为固定值,表明系统可能不绝对趋于平衡位置,但有较大概率收敛到平衡位置．图1(b)为图1(a)的俯视图,整体呈圆环状,最内环的红色区域对应图1(a)最高区域为有限值．如图1(c)所示,当噪声强度D=0.2时,联合概率密度函数高度下降、宽度增加,形状由单峰变为火山口,与图1(a)相比,此时系统(11)的性态发生了改变,即系统发生P-分岔,在这种情形下,系统的广义变量φ和η可能不为零,系统变得不稳定．图1(d)为图1(c)的俯视图,俯视图中最内环红色区域对应值减小,圆环整体扩大,很形象地说明了函数p(φ,η)的变化趋势．当噪声强度D=0.3时,联合概率密度及俯视图分别如图1(e)、1(f)所示,函数p(φ,η)这种变化趋势更加明显,这也意味着系统的广义变量φ和η都可能增大,系统(11)变得更加不稳定．

噪声强度D分别为0.2, 0.3, 0.4和0.5时,平稳概率密度函数如图2所示．根据图2可以看出,随着噪声强度D的不断增大,概率密度函数的顶点减小,函数形状趋于平缓,变化趋势与联合概率函数的变化趋势形成对应,这也表明系统性态改变愈发明显．另外,在系统发生P-分岔时,概率密度函数图形由单峰变为双峰,此时广义变量φ和η的收敛解的变化,一定程度上可反应系统(1)变量的收敛情况,如角速度ω变化反馈到永磁同步电动机实际运行中,可能是平稳转动状态到异常转动状态的临界点,概率密度函数趋于平缓的过程中,方程(11)解变得发散．在实际运行中,永磁同步电动机可能会发生转速不稳定的现象．

图2 不同噪声强度D下的平稳概率密度图Fig. 2 The stationary probability density function with the change of noise intensity D

为进一步探讨噪声强度的影响,除对概率密度函数分析外,我们还对系统进行动力学行为分析．固定无量纲化参数γ=130,Ud=3,Uq=10,Tm=5,选取σ作为分岔参数,讨论不同噪声强度值下变量x的分岔如图3所示．从图3(a)中可以看出,在未引入噪声前,系统(3)在区间σ∈[10,24.18]范围内表现出伴随混沌的加周期分岔行为, 其中区间[16.75,17.14]和[21.11,21.54]分别为2周期和3周期窗口, 当参数σ大于24.18时,系统从周期6→周期12→周期6→周期3．当噪声强度D=0.1时,相较于图3(a),图3(b)中周期窗口由稳定状态变为轻微振荡,随着噪声强度D的增加,这种不稳定性进一步增强．由图3(c)和图3(d)可以看出,系统几乎变成完全混沌状态,这证实了上述结论的有效性．

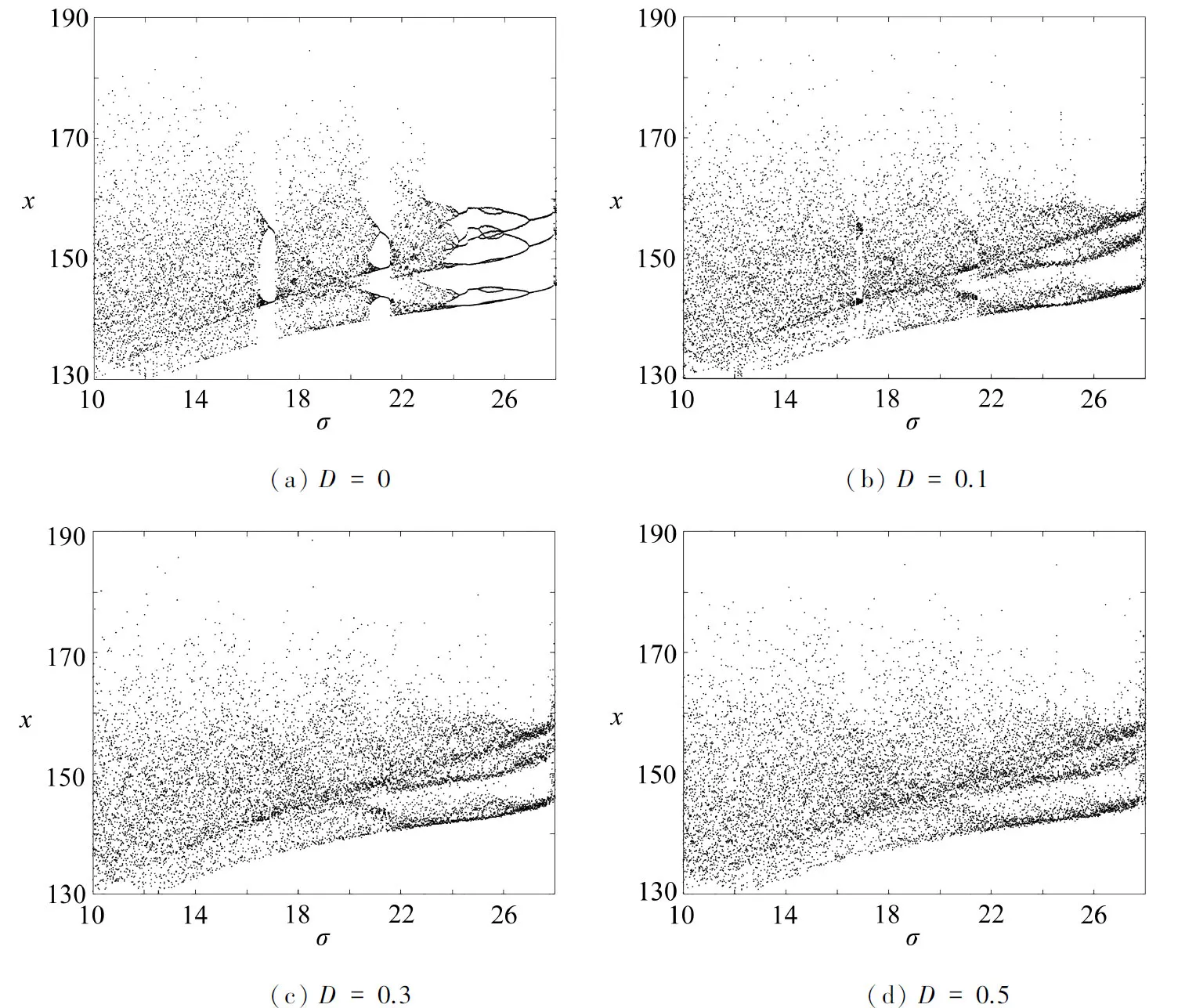
图3 不同噪声强度D下的系统分岔图Fig. 3 The bifurcation diagram with the change of noise intensity D

3 双参数分岔

永磁同步电动机系统在运行过程中可能会受到随机因素的干扰,这些干扰可能导致两个甚至多个参数同时发生变化．所以对系统(3)在双参数空间中研究分岔结构更具有参考意义．本节保持参数值不变,采用四阶随机Runge-Kutta算法进行数值模拟,用500×500相同距离点覆盖,如图4所示．图中的图例颜色栏标记了不同数字,代表不同的振荡状态,左图图例表示周期数,右图图例表示Lyapunov指数．另外,在图4(a)和4(b)的左图中,白色区域表示周期数大于19的周期振荡状态或混沌状态．

(a) σ∈[10,30], Ud∈[-5,80]

图4(a)左图为系统(3)变量x在参数σ∈[10,30],Ud∈[-5,80]平面上的分岔图,如图所示右上方黄色区域为稳定态区域,首先通过Hopf分岔生成1周期吸引子,并由倍周期分岔进入广泛的白色振荡区域．由于仿真精度所限,无法确定该振荡区域是拟周期振荡态或是混沌态,我们的思路是计算对应的最大Lyapunov指数值[23]．图4(a)右图为左图分岔结构对应的最大Lyapunov指数,其中绿色区域为最大Lyapunov指数值远小于零的稳定态,黄色区域表示最大Lyapunov指数值在区间[-0.001,0.001]周期振荡状态,红色区域为混沌态．对图4(a)综合分析,在参数平面上右上方稳定态经倍周期分岔最终进入混沌状态,值得关注的是,混沌区域内镶嵌了一些“鱼”形周期区域,且它们呈分形结构．参数σ∈[15,35],Uq∈[-5,30]平面上系统分岔图与其最大Lyapunov指数图见图4(b)．周期振荡区域通过倍周期分岔方式进入混沌区域,类似地,混沌区域镶嵌着很多 “鱼”形周期区域．

我们接下来讨论噪声激励对分岔的影响,参数σ∈[10,30],Ud∈[-5,80]平面上不同噪声强度D下的最大Lyapunov指数图见图5．图5(a)、5(b)分别为噪声强度D=0和D=10-8时的情形．对比两图可以看出,最大Lyapunov指数的值没有发生显著改变,则系统对低强度白噪声具有一定的抗干扰性．如图5(c)所示,当噪声强度为D=10-6时,“鱼”形周期区域受到侵蚀尾部演变为混沌态,有趣的是,“鱼”形结构的头部却保持原本特征,这说明“鱼”形结构不同区域鲁棒性也有差异．如图5(d)所示,当噪声强度为D=10-4时,这种演化趋势更加明显,“鱼”形周期区域几乎完全变为混沌态．此外,对比观察图5发现,大范围黄色“带”状周期振荡区域并未发生明显收缩,这说明在不同周期振荡区域,抗干扰性也不同．值得注意的是,图5(d)中部分黄色周期振荡区域变为绿色收敛状态,这也说明了噪声对系统影响的两面性．它不仅可以破坏“鱼”形周期振荡区域,使其混沌态,还可以使周期振荡区域转变为收敛态．从上面的分析可以看出,噪声对系统的周期振荡区域有显著的影响,但通过优化参数也可诱导周期振荡区域产生收敛振荡行为．

图5 随噪声强度D变化的最大Lyapunov指数图Fig. 5 The largest Lyapunov exponent diagram with the change of the noise intensity

4 结 论

本文研究了永磁同步电动机系统在Gauss白噪声扰动下的分岔问题,根据数值模拟结果,随着噪声强度

D的不断增大,联合概率密度函数由单峰状变为火山口形状,即系统发生P-分岔．同时平稳概率密度函数顶点降低坡度变缓,这也说明系统稳定性的改变．对永磁同步电机系统进一步研究发现：它在双参数空间中具有分形结构的“鱼”形周期区域,大量数值模拟结果证实了白噪声强度对该周期区域的边界具有更强的侵蚀作用．值得注意的是,大范围黄色“带”状的周期区域对白噪声却表现为很强的鲁棒性,特别地,白噪声能够诱导周期振荡使其产生收敛的振荡行为．此外,这些研究方法可以直接应用到白噪声对其他系统的相关研究中,以便其与本文所得出的结论进行对比．