三维快速多极边界元法分析地埋管群传热问题

宋子欣, 胡宗军, 胡 斌, 牛忠荣

(合肥工业大学 土木与水利工程学院, 合肥 230009)

0 引 言

地埋管换热器的埋置深度一般在30～200 m之间,埋管管径为25～100 mm,壁厚为2～6 mm,U型管道狭长,涉及到薄壁结构与周围土体耦合问题,导致换热分析较为困难．为此,国内外学者对其传热问题进行了诸多研究．Guan等[1]将U型管通过等效公式简化为矩形管,略去了U型管管底区域,在此模型下讨论了地下水渗流速度对埋管传热的影响．Kerme等[2]利用能量平衡方程分析了具有两个独立回路的双U管的瞬态传热过程,得到了沿钻孔深度分布的传热曲线．贺泽群等[3]采用自适应负荷法,以钻孔壁温度替代管内壁温度,对不同钻孔位置的换热量和热堆积问题进行了研究．张荻等[4]采用实验和数值模拟相结合的方法,研究了层流条件下球窝结构内矩形通道内部的流动与换热特性．朱利媛等[5]考虑热量沿轴向的传递,利用边界元法对二维稳态热传导下的地埋管换热器进行了模拟研究．Lei等[6]将U型管简化为三维曲线,利用有限元软件COSMOL建立了地埋管群的热渗耦合三维数值模型,研究了系统运行一年后地层温度场的变化．

目前,多数学者是利用有限元法(FEM)对地埋管换热器进行模拟研究．在FEM中有无限单元、管道单元和基于连续体的壳单元等,用于计算薄体和厚体耦合的传热问题．其中无限单元一般用于解决土壤无限域问题,和常规有限元一起用来解决更复杂的无界问题．同时,对于模拟接触问题,基于连续体的壳单元由于考虑了厚度的变化,与常规壳单元相比更加精确．相比于FEM,边界元法(BEM)只需在结构的表面和界面上划分网格,缩减了网格的自由度数量,因此在分析薄体问题时具有优势．但传统BEM生成的定解方程组的系数矩阵是非对称满秩矩阵[7],计算量级过大,难以计算大规模问题,因此传统BEM无力计算地埋管群的传热问题．随着快速多极算法的发展,应运而生的快速多极边界元法(FMBEM)提高了传统BEM的计算效率,并降低了内存的占有量,近二十年被广泛应用于解决各种大规模问题．由于FMBEM在使用线性单元和高阶单元时,八叉树结构中存在同一单元的节点处于不同叶子的现象,导致单元积分难以处理．因此目前FMBEM主要采用常值单元,在处理薄体结构和高梯度场时,需布置稠密网格以弥补计算精度的不足,导致计算效率较低．徐刚等[8]将传统常值单元中直接布置在流体计算域表面网格中心上的奇点移到了计算区域外部,以此实现了无奇异化．刘静等[9]基于自适应分块技术,提出了一种组合变换法,分别消除了径向和角度方向积分的近奇异性．侯俊剑等[10]利用扩展单元插值法,在不连续的边界配置虚拟节点,利用虚拟节点插值边界上连续和不连续的物理场,将非连续单元变为高阶连续单元．胡宗军等[11]针对二维位势问题,通过在几乎奇异积分单元上扣除奇异函数部分消除了几乎奇异性,并将其应用于二维薄体结构温度场分析中．

本文基于边界元法基本理论,引入三维线性单元几乎奇异积分的正则化算法[12],解决了线性单元跨叶子积分难题,对三维位势问题建立了三角形线性单元FMBEM和计算程序,大大提高了FMBEM分析大规模三维薄壁热传导问题的计算效率和精度．文中采用三角形线性单元FMBEM对地埋管换热器的换热性能进行分析,讨论了管壁厚度对地埋管传热性能的影响,并研究了地埋管群的传热效率．本文研究成果可为地源热泵的设计和运行提供参考．

1 三维位势问题快速多极边界元分析与数值验证

1.1 边界元法分析稳态热传导的基本方程

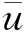
(1)

(2)

(3)

式中r=|y-x|为源点y到场点x的距离．

采用3节点三角形面单元对计算域边界进行离散．在直角坐标系Ox1x2x3中建立如图1所示的局部参考坐标系oξη,对单元Γe的几何坐标、位势以及热流进行插值,单元Γe上场点x的坐标xi可以表达为

图1 参考坐标系Fig. 1 Reference coordinate systems

(4)

式中形函数Nm为

(5)

其中A为三角形单元面积,am,bm,cm为常数,由3节点局部坐标表示．

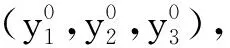
ξ-ξ0=ρcosθ,η-η0=ρsinθ．

(6)

将式(6)代入式(4),有

(7)

(8)

因此,源点y与场点x之间的距离r可表示为

(9)

式中

(10)

用边界单元离散后,边界积分方程表达式(1)变为

(11)

式中f为边界单元总数．让源点y遍历所有边界节点,则边界积分方程(11)转化为代数方程

Az=B,

(12)

其中A为系数矩阵,z为未知量,B为已知量．引入已知边界条件,即可由方程(12)求得所有未知的边界节点位势u(x)和热流q(x)．上述方程若采用直接法或迭代法求解,如网格数量众多,则系数矩阵A需要极大的存储量,计算量也快速增长．

这里的快速多极边界元法将式(11)中线性单元积分划分为两类： 远场单元积分和近场单元积分．近场单元积分是指源点离单元较近的积分, 包含有奇异积分、 几乎奇异积分和非奇异积分．本文采用Gauss数值积分计算非奇异积分; 采用常位势场法计算奇异积分, 而对于几乎奇异积分采用半解析算法[12], 具体过程如下．

将式(8)和式(9)代入式(2)、(3),离散后的积分形式为

(13)

随着式(10)中e1的减小,式(13)的积分产生几乎奇异性,常规Gauss数值积分失效．对式(13)的变量ρ做积分,令

(14)

并对式(14)反复运用分部积分,因Qn(ρ,θ)为ρ的多项式,在三维位势问题中,于线性单元而言,对ρ求导必有

(15)

因此,反复运用分部积分后,式(13)转化为

(16)

其中ρ(θ)由单元Γe的3个边的极坐标表达式决定．式(16)已将式(13)的面积分转化成一系列关于变量θ的线积分,积分的几乎奇异性消失,可利用常规Gauss数值积分计算．

对于远场单元积分,FMBEM通过对基本解(2)和(3)进行双球谐函数展开,用自适应树结构代替传统矩阵,减少了计算量和存储量．基本解U*(x,y)在球坐标系下的多极展开式[13]为

(17)

(18)

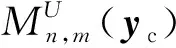
(19)

将基本解Q*(x,y)按同样方法展开,有

(20)

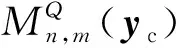
(21)

由式(18)—(21)可以看出,场点x由中心点yc传递到源点y,避免了每个源点都要对每个场点进行单独积分计算,因此FMBEM在形成式(12)系数矩阵A时大幅度减少了计算量．

目前FMBEM主要采用常值单元[14],因而没有几乎奇异积分计算的难题．本文将三角形面单元几乎奇异积分处理技术[15]与三维边界元快速算法结合,创立了三维位势问题三角形线性面单元FMBEM,并研制了计算程序．本文三角形线性面单元FMBEM算法显著提高了三维位势边界元法的计算精度和效率,能够胜任大规模三维薄体结构的热传导分析．

1.2 多介质传热模型FMBEM分析

采用三角形线性面单元FMBEM程序,分析图2所示双层圆筒壁结构的热传递问题．r1=8 mm,r2= 10 mm,r3=11 mm,圆筒沿Z方向深20 mm,Ω1,Ω2两个区域的导热系数分别为9.93 W/(m·℃)和0.5 W/(m·℃),圆筒最内侧壁面温度T=100 ℃,最外侧壁面热流q=21.33 W/m2,其余表面绝热,热流q=0 W/m2．

图2 双层圆筒壁结构Fig. 2 The double cylinder wall structure

对结构表面和界面按照三角形面单元进行离散,如图3所示,为做对比分析,分别给出了3种网格模型： ① 具有10 327个节点、20 864个单元的稀疏网格模型; ② 具有16 036个节点、32 324个单元的常规网格模型; ③ 具有36 793个节点、74 004个单元的加密网格模型．

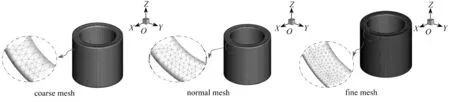
图3 双层圆筒壁网格模型Fig. 3 Double-layer cylindrical wall mesh models

图4给出深度Z=10 mm位置,沿AB路径的3种网格模型通过FMBEM程序计算所得温度TFMBEM以及与解析解温度Ta的相对误差Δ,其中r为AB路径上的点到圆心的距离：

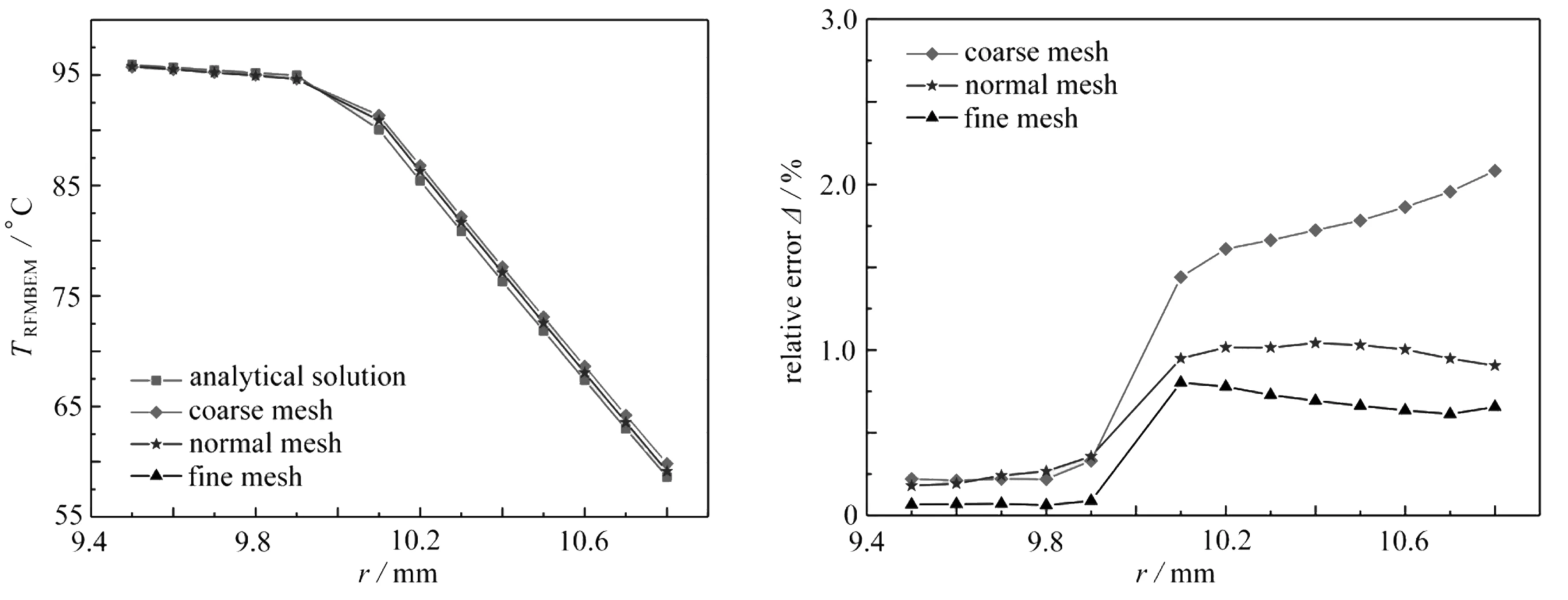
图4 FMBEM在Z=10 mm处沿AB路径计算所得温度TFMBEM及相对误差ΔFig. 4 Temperature TFMBEM and relative error Δ calculated with the FMBEM along the AB path at Z=10 mm

对稀疏网格模型,本文算法计算得到的各点温度与解析解相比,在r大于9.9 mm后相对误差Δ增大,但不超过2.1%;对常规网格模型和加密网格模型,本文算法的温度计算结果基本一致,且与解析解的相对误差Δ不超过1.05%．计算结果表明本文算法计算三维热传导问题时,采用常规网格即可获得较高的计算精度．

2 U型地埋管换热器的FMBEM分析

2.1 U型管计算假定及设计参数

地源热泵系统中,U型地埋管换热器和土壤之间的实际传热关系复杂,现采用三角形面单元FMBEM程序计算其换热性能．本文对地源热泵系统做以下假设：

1) 将土壤看成连续均匀的各向同性物质,土壤的热物性在整个换热过程中保持不变．

2) 假设土壤地下温度保持恒定,不受地面气温的影响[16]．

3) 水的热扩散率比土壤低2～4个数量级[17],因此在地埋管换热器的传热过程中,忽略土壤中水分和溶质的转移,即不考虑地下水渗流的影响．

4) 忽略管道内流体和地埋管管内壁之间的对流换热热阻,假设管内壁温度为流体温度,且温度沿管埋深线性变化．在U型管底部区域温度恒定,为进水与出水温度的平均值．

计算模型中,土壤区域和回填区域上表面均绝热,热流q=0 W/m2,其余设计参数如表1所示．

表1 地埋管换热器设计参数

在U型地埋管换热器中,管壁厚度远小于回填区域和土壤区域的尺寸,一般计算方法难以考虑U型管管壁厚度对换热的影响,而边界元法具有降维特性,FMBEM只需在结构表面和界面上划分网格,特别适用于厚体和薄体区域的耦合问题．在制冷和制热两种工况下,本小节研究了不同的管壁厚度对单U型地埋管换热量的影响．取管外直径为32 mm,管材为聚乙烯,导热系数为0.4 W/(m·℃),其他计算参数如表2所示．U型地埋管的FMBEM计算模型见图5,共有23 113个节点和46 256个三角形面单元．

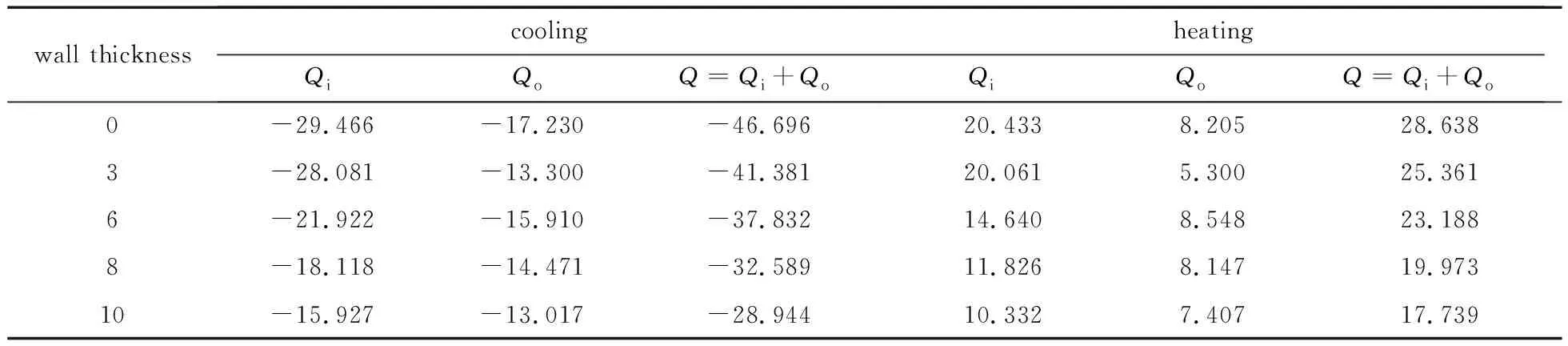
表2 不同管壁厚度时地埋管单位井深换热量(单位： W/m)

采用FMBEM计算得到各点的温度及热流密度．然后根据U型管内壁的热流计算地埋管换热器单位井深换热量：

(22)

其中Si为U型管内壁上第i个三角形单元Гi的面积,qi为FMBEM计算所得单元Гi平均热流密度(三角形单元3个节点热流均值),m为U型管内壁面所划分的单元总数,L为地埋管埋置深度．

不同管壁厚度时,通过FMBEM程序计算得地埋管单位井深换热量如表2所示,其中Qi,Qo分别为进、出水管单位管长换热量,Q=Qi+Qo为单位井深换热量．由表2可知,随着管壁厚度增加,地埋管单位井深换热量逐渐减小．制冷条件下,当管壁厚度为10 mm时,单位井深换热量为28.944 W/m,与管壁厚度为3 mm时的单位井深换热量41.381 W/m相比,减小了30.05%;与不考虑管壁厚度时的单位井深换热量46.696 W/m相比,减小了38.02%．制热条件下,当管壁厚度为10 mm时,单位井深换热量为17.739 W/m,与管壁厚度为3 mm时的单位井深换热量25.361 W/m相比,减小了30.05%;与不考虑管壁厚度时的单位井深换热量28.638 W/m相比,减小了38.06%．

按我国对地埋管管道外径及壁厚尺寸的规定[18],当管外径小于40 mm时,壁厚应为3 mm．由表2可知,制冷条件下,管壁厚度为3 mm时,单位井深换热量为41.381 W/m,与不考虑管壁厚度时的单位井深换热量46.696 W/m相比,减小了11.38%;制热条件下,当管壁厚度为3 mm时,单位井深换热量为25.361 W/m,与不考虑管壁厚度时的单位井深换热量28.638 W/m相比,减小了11.44%．

为反映管壁厚度对换热的影响,图6分别给出制冷、制热两种工况下,不考虑管壁厚度和管壁厚度为10 mm时,地埋管回填土壤区域在底部边界的温度分布局部图．由图6可知,当管壁导热系数小于土壤和回填材料的导热系数时,管壁热阻是阻碍地埋管换热的主要因素之一,讨论地埋管换热器的换热量时,不应忽略管壁厚度对其产生的影响,否则会造成较大误差．当管壁导热系数一定时,管壁越厚,对管内流体和土壤之间的换热影响越大,计算时考虑管壁厚度产生的影响,会得到更符合工程实际的结果．当管壁导热系数小于土壤导热系数时,在保证U型管结构强度满足要求的前提下,管壁应尽量薄,以减小其热阻对地埋管换热器产生的负面影响．

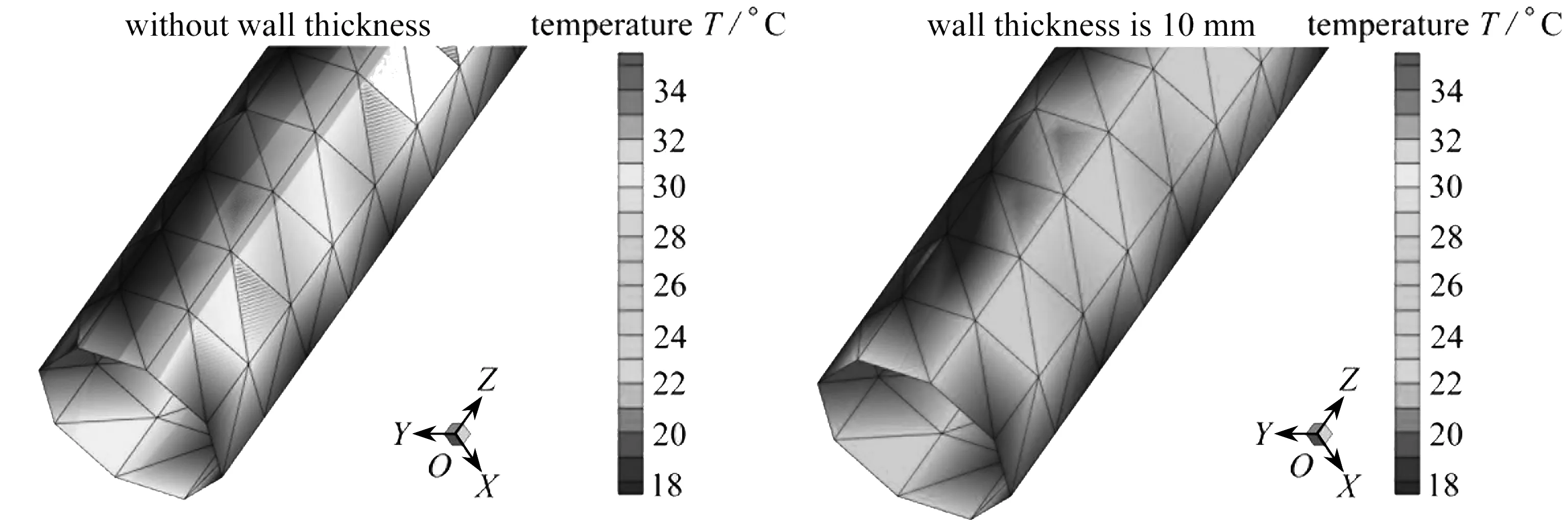
(a) 制冷工况时FMBEM计算结果温度分布图(a) Calculation results of temperature during cooling

2.2 多孔管群换热器的FMBEM分析

在工程应用中,地源热泵地埋管换热器系统通常都是以多管井即管群的形式出现．由于各埋管之间存在热相互作用,因此管群的换热特性与单U型地埋管相比有明显区别,单U管的结论不能直接应用于大型管群换热分析．本文采用FMBEM对地埋管换热器管群系统进行分析,讨论管群之间的热干扰现象．

考虑4(横向)×4(纵向)等间距排列管群在不同工况下的运行情况, 利用对称性取1/4结构, 以分析含16个管井的U型管群换热性能．取土壤半径为15 m, 土壤区域内分布有4组U型管井, 各管井中心间距为5 m,井深50 m．模型坐标原点位于对称中心,靠近坐标原点的管井,其中心距两坐标轴均为2.5 m,为①号管井．②号管井坐标位于(-7.5 m, 2.5 m),③号管井位于(-2.5 m, 7.5 m),④号管井位于(-7.5 m,7.5 m)．

本例中钻孔区域内部采用原土回填,即土壤和回填土的导热系数均为2.0 W/(m·℃)．U型管外径32 mm,管壁厚3 mm,两管腿中心间距50 mm．利用三角形面单元对结构表面和界面进行离散,共生成58 785个节点,117 670个单元,如图7所示．土壤上表面与对称面绝热,外表面温度18 ℃,其余计算参数如表2所示．利用FMBEM程序计算得制冷、制热两种工况下各管井单位井深换热量,如表3所示．其中Qi,Qo分别为进、出水管单位管长换热量,Q=Qi+Qo为单位井深换热量．

表3 壁厚3 mm时4×4管群单位井深换热量(单位： W/m)

由于此管群模型有16个管井,呈对称形式,因此将管井分为3类,中心的4个管称为中井,离中心最远位置的4个管称为角井,除了角井之外的四周的管称为边井．

由表3可知,对于4×4地埋管管群,制冷工况下,中井单位井深换热量为9.431 W/m, 与角井的单位井深换热量23.855 W/m相比, 减少了60.47%; 制热工况下, 中井单位井深换热量为6.434 W/m, 与角井的单位井深换热量14.627 W/m相比, 减少了55.78%．边井与角井相比,单位井深换热量在制冷工况下分别减少了32.61%和27.57%,在制热工况下分别减少了31.36%和27.49%．中井位于土壤中心, 周围存在的其他管井同土壤的换热导致土壤中心区域温度变化, 减小了中井内流体与其周围土壤的温差, 降低了中井的换热效率．图8给出了4×4管群在制冷、制热两种工况下的温度云图,由温度云图可以看出,在两种工况下,角井内流体与周围土壤的温差均大于中井．因此,管井与管井之间产生了热量的互相干扰,周围管井对中心管井产生的热干扰阻碍了中心管井沿径向传热．因角井周围毗邻无限大土壤区域,热扩散条件优于其他区域管井,受到的热干扰影响最小;边井附近除了无限大土壤区域,还受到角井和中井的影响,热扩散条件较差,导致其换热量下降;中井被其他管井所包围,换热量最低,在夏季工况下只有角井换热量的39.53%,冬季工况也仅达到了角井换热量的44.22%．

(a) 制冷工况时FMBEM计算结果温度分布图(a) The FMBEM calculation results of temperature during cooling

为直观地比较管群间的热相互影响,图9给出了在制冷、制热两种工况下,单U型地埋管与①至④号管井及4×4管群单位井深换热量的对比．由图9可知,制冷工况下,与单U型地埋管单位井深换热量40.607 W/m相比,4×4管群的单位井深换热量为266.556 W/m,提高了556.43%;制热工况下,与单U型地埋管单位井深换热量24.883 W/m相比,4×4管群的单位井深换热量为166.828 W/m,提高了570.99%．中井在制冷工况下的单位井深换热量为9.431 W/m,相较于单U型地埋管换热量降低了76.77%;在制热工况下的单位井深换热量为6.434 W/m,相较于单U型地埋管换热量降低了74.01%．角井在制冷工况下的单位井深换热量为23.855 W/m,比单U管换热量降低了41.25%,制热工况下的单位井深换热量为14.627 W/m,比单U管换热量降低了41.22%．

图9 4×4地埋管群单位井深换热量对比Fig. 9 Comparison of heat transfer fluxes of 4×4 buried pipe groups

由此可见,对于地埋管管群而言,周边区域埋管的热扩散条件显著优于中心区域埋管,在管内流体温度相同时,周边区域埋管承担了较大的换热负荷．中心区域埋管受到周边区域埋管热干扰的影响较大,导致土壤中心区域地埋管换热器换热效率低下．

为研究管壁厚度对管群换热量的影响,表4给出了4×4管群在不考虑壁厚时换热量的计算结果,其中管径为32 mm．表4结果表明,制冷工况下,不考虑壁厚时4×4管群总换热量为289.016 W/m,与壁厚3 mm时4×4管群总换热量266.556 W/m相比,提高了8.43%;制热工况下,不考虑壁厚时4×4管群总换热量为193.060 W/m,与壁厚3 mm时4×4管群总换热量166.828 W/m相比,提高了15.72%．因此,对管群进行模拟计算时,考虑管壁热阻十分必要．若忽略管壁热阻产生的影响,会造成较大的计算误差．表3、4对比表明,换热量增加主要是由于中井和角井的贡献．因此,于管群而言,提高换热量的主要措施在于降低埋管之间的热相互作用,同时减少中井和角井的管壁厚度．

表4 不考虑壁厚时4×4管群单位井深换热量(单位： W/m)

3 结 论

本文基于线性单元,克服单元跨叶子积分难题,针对边界元法在奇点附近区域因存在奇异积分而产生的误差,将三维位势问题快速多极边界元法与几乎奇异积分的半解析算法相结合,创立了一种精确高效的快速多极边界元新算法,使得边界元法能够有效分析大规模三维薄体结构热传导问题．应用本文算法对考虑了管壁厚度的地埋管换热器三维模型进行计算,分析讨论了单U型地埋管换热器和管群换热器的传热性能．所得结论如下：

1) 管群中,管与管之间产生的热干扰会阻碍热量的传递,导致中心区域管井换热效率低下,且管群规模越大,管与管之间热干扰现象越强烈,提高管群换热量的主要措施是降低热干扰的同时减少壁厚．

2) 管壁的厚度是影响地埋管换热效率的主要因素之一．在讨论地埋管换热器的换热量时,对管壁的影响因素加以考虑,方可得到更符合工程实际的结果．

3) 本文中对曲面结构表面采用平面单元进行网格划分,若采用曲面单元划分网格,则有可能进一步减小问题的自由度数,同时提高计算精度．