基于L-S广义热弹性理论YSZ在超短脉冲下的热力响应

赵 颐, 田晓耕

(西安交通大学 机械结构强度与振动国家重点实验室, 西安 710000)

0 引 言

近年来,随着激光技术的不断发展,其脉冲宽度已经可以短至皮秒、飞秒量级,属于超短脉冲的范畴．超短脉冲激光可以实现对硬脆材料的精密加工,在打孔、切割、划线、沉积成型等高精度微加工领域有着广大的应用前景[1-3]．目前,对于激光加工的优化,多通过重复实验寻找合适的加工参数[4],存在成本高、效率低、适用范围小的问题．通过研究硬脆材料在超短脉冲激光作用下的热力响应,探究不同物理量在多脉冲作用下的演化规律,获得相关参数对响应的影响,预测加工时工件内部的动态响应,对于优化加工参数具有重要的指导意义．

对于超短脉冲激光加工热力响应的研究,大多在简化真实物理过程的基础上建立数学模型,利用有限元方法对物理场进行求解,这导致所得到的结果不能准确地描述材料的热力响应．Shen等[5]研究了YSZ发生固体相变过程中的动态响应．秦渊等[6]建立了毫秒激光打孔的轴对称模型,并对材料从发生固体相变到熔融去除过程中的孔形状变化进行了研究．由于聚焦后较强的超短脉冲激光能量在空间上服从Gauss分布[7-8],发生锥形辐射使研究激光作用材料的温度分布变得复杂,Rahaman等[9-10]利用三角波代替Gauss分布,并阐述了其合理性,得到了瞬态二维热传导的解析解．值得注意的是,上述研究均采用经典Fourier传热定律(扩散方程描述变量以无限速度传播),而超短时等极端条件下热以有限速度传播,经典Fourier定律无法给出准确的响应预测[11]．对于这类极端条件下的热力耦合问题,应采用以非Fourier传热为基础的广义热弹性理论进行求解．包立平等[12]讨论了激光等离子体产生的波模型,应用摄动法给出了金属板中非Fourier和Fourier温度场的关系．谭胜等[13]基于双相延迟模型[14]对飞秒激光烧蚀金属的现象进行了数值模拟,获得了与实验结果一致的预测．也有学者采用分子动力学方法对固体在超短脉冲作用下的热力响应进行了研究,如Xiong等[15]研究了铜薄膜在超短脉冲下的热力响应;Li等[16]研究了氩晶体在皮秒激光烧蚀过程中的相变．

现有研究中,多采用Fourier热传导定律,或是未考虑多次脉冲带来的影响,对材料的热力响应不能准确描述．本文验证有限元解法的可靠性后采用以C-V传热模型[17-18]为基础的L-S广义热弹性理论[19]对YSZ材料在多脉冲作用下的瞬态热力响应开展了研究．讨论了不同脉冲间隔、材料比热容随温度变化等对热力响应的影响．最后,讨论了激光脉冲作用下机械波经边界反射后在材料内部的演化．

1 基 本 方 程

本文基于L-S广义热弹性理论,其控制方程如下．几何方程为

(1)

本构方程为

σij=λεkkδij+2Gεij-γΘδij;

(2)

各向同性材料不计体力的运动方程为

(3)

温度控制方程为[20]

(4)

式中,εij为应变分量,ui为位移分量,σij为应力分量,ρ为材料密度,λ和G为Lamé常数,δij为Kronecker指标,Θ=T-T0,T为绝对温度,T0为参考温度,κ为热传导系数,γ=(3λ+2G)αt,αt为线性热膨胀系数,

∇2为Laplace算子,τ为热松弛时间,cE为材料比热容,Q为热源．

考虑超短脉冲作用时可简化为二维轴对称模型,在柱坐标系下改写方程(1)、(3)、(4)可得几何方程为

(5)

运动方程为

(6)

温度控制方程为

(7)

式中,u和w分别为r方向和z方向的位移．对于时间与空间尺度都很小的超短脉冲问题,为了便于分析,引入以下无量纲量：

(8)

将式(8)代入式(1)—(4),可得轴对称模型下L-S理论的无量纲控制方程．运动方程为

(9)

本构方程为

(10)

温度控制方程为

(11)

2 YSZ在超短脉冲激光作用下的热力响应

目前,求解广义热弹性问题常用的方法有积分变换[21-23],即借助于Laplace变换和Fourier变换将控制方程转化至频域内求解后再进行积分反变换得到时域内的解．此方法需要进行两次积分变换,而且数值积分反变换会引入离散和截断误差,使得热的波动性不能被精确捕捉[24]．还有学者采用正则模态法对一些问题进行了解析求解[25-28],以达到迅速解耦的目的．上述方法求解广义热弹性问题时,多限于相对简单的物理模型与热载荷情况,对于热载荷形式相对复杂的问题,积分变换及解析求解均面临着不同程度的数学困难．因此,采用有限元(FlexPDE)直接在时域对控制方程进行求解是一种有效的方法．

考虑超短脉冲激光轮廓迂回法打孔的工况,将打孔过程简化为圆柱受到多次脉冲载荷作用的过程．部分材料参数如下[5,29]：

ρ=6 100 kg/m3,G=48.4 GPa,λ=48.4 GPa,

κ=2.09 W/(m·K),αt=9.4×10-6K-1,T0=294 K．

根据Vedavarz等[30]的研究,YSZ的热松弛时间为

(12)

式中,v为固体中的声子速度,为了简化计算,可取固体中的声速近似代替,本文取v=5 842 m/s．将式(12)代入式(8),可得无量纲松弛时间为

(13)

激光脉冲的能量函数为

(14)

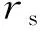
有限元计算时,模型(如图1)四周取绝热边界,其力学边界条件上下表面应力自由、周边固定,可表示为

(15)

初始条件为

(16)

为简化表述,在不引起混淆的情况下,下文将去除无量纲量的上标“～”．

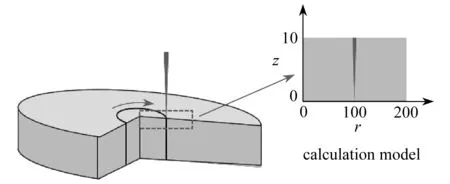
图1 轮廓迂回法打孔示意图Fig. 1 Schematic diagram of contour roundabout punching

2.1 有限元求解准确性验证

为验证有限元求解的准确性,首先利用有限元方法对不计体力两端固定且绝热的均匀各向同性杆在移动热源作用下的热力响应问题进行求解,并与文献[20]结果进行对比．边界条件、材料参数均与文献中相同．由于文献中热源项包含Dirac函数,为使有限元模拟描述的问题与文献一致,根据Dirac函数的性质,移动热源可表示为

(17)

式中,A为积分系数,d为移动热源在x方向的宽度,满足A·d=0.5．本文取d=0.1,因此有A=5．f(a1,a2)为脉冲函数,满足

(18)

有限元求解时,采用自适应网格,不满足精度要求时,网格加密重新计算．图2、3分别给出了热源移动速度为2、热松弛时间为0.05时的温度和应力结果．从图中可知,有限元所得结果与解析解吻合较好,说明有限元解法可以得到准确的解答．

2.2 比热容为常数

由于深度对热源作用附近的应力分布并无影响[31],本文中在竖直方向施加与z无关的热源．首先分析比热容为常数时(cE=453)多脉冲激光作用下YSZ的热力响应以及周期为6、不同脉宽(无量纲脉宽取2,3,4)对热力响应的影响,如图4所示．

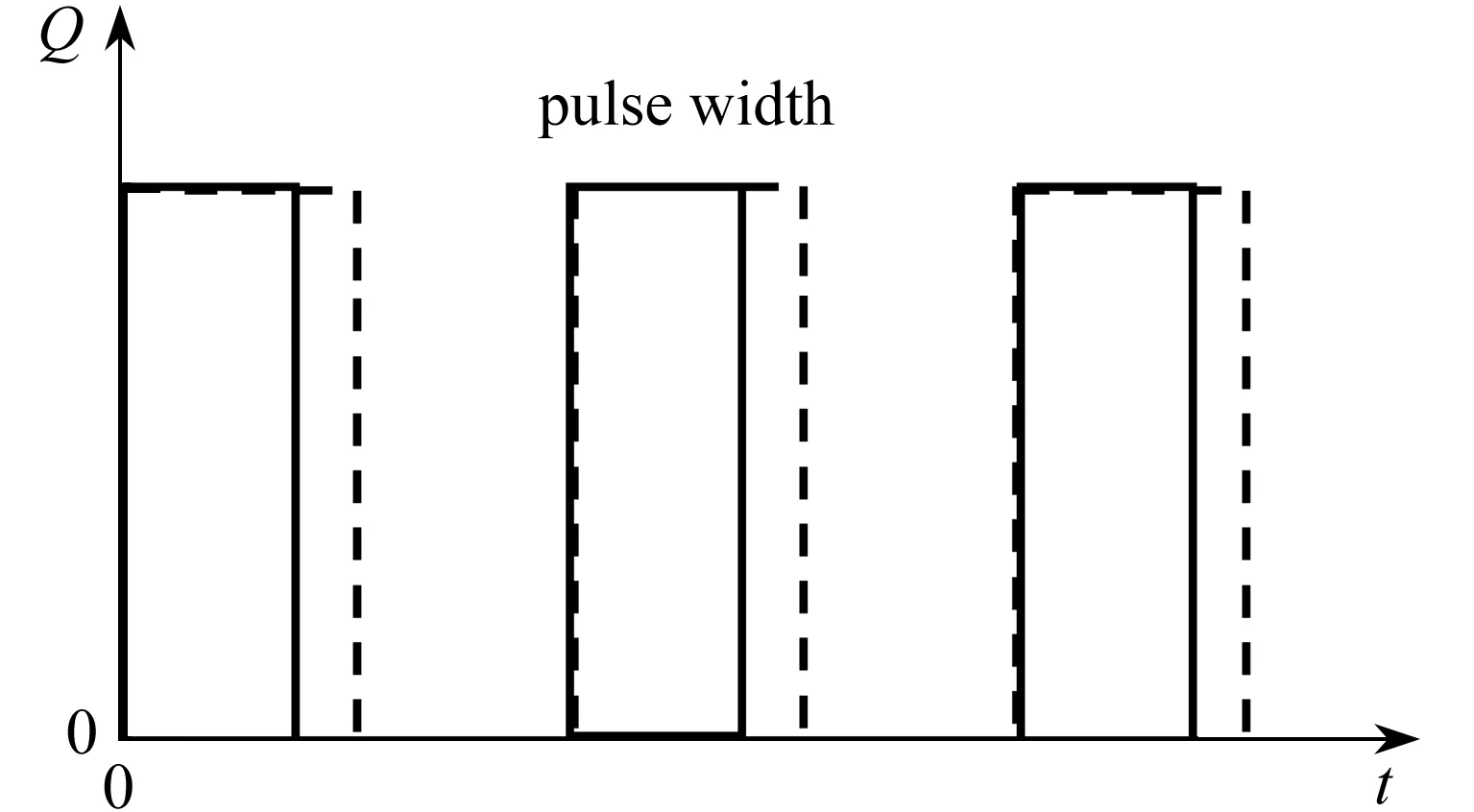
图4 激光脉冲随时间的变化Fig. 4 The variations of laser pulses with time

脉宽为2时,z=5处响应的径向分布如图5(a)、5(b)所示．脉宽为2时,t=14是热源刚消失的时刻,t=18是下一次热源刚出现的时刻．由图5(a)可知,热松弛时间的存在导致热源刚作用后系统的温度并未达到一个周期内的最大值,而是在弛豫之后达到温度的顶峰．由图5(b)知,在热源激励下,热源内外两侧材料均受压,且位移随时间不断增大．从应力分布曲线中可以看出,随着脉冲次数的增多,σrr出现多个压应力峰值,而σθθ在应力波波前出现一个“应力平台”,经过平台后再下降至0,整个应力曲线的变化规律与温度相似．

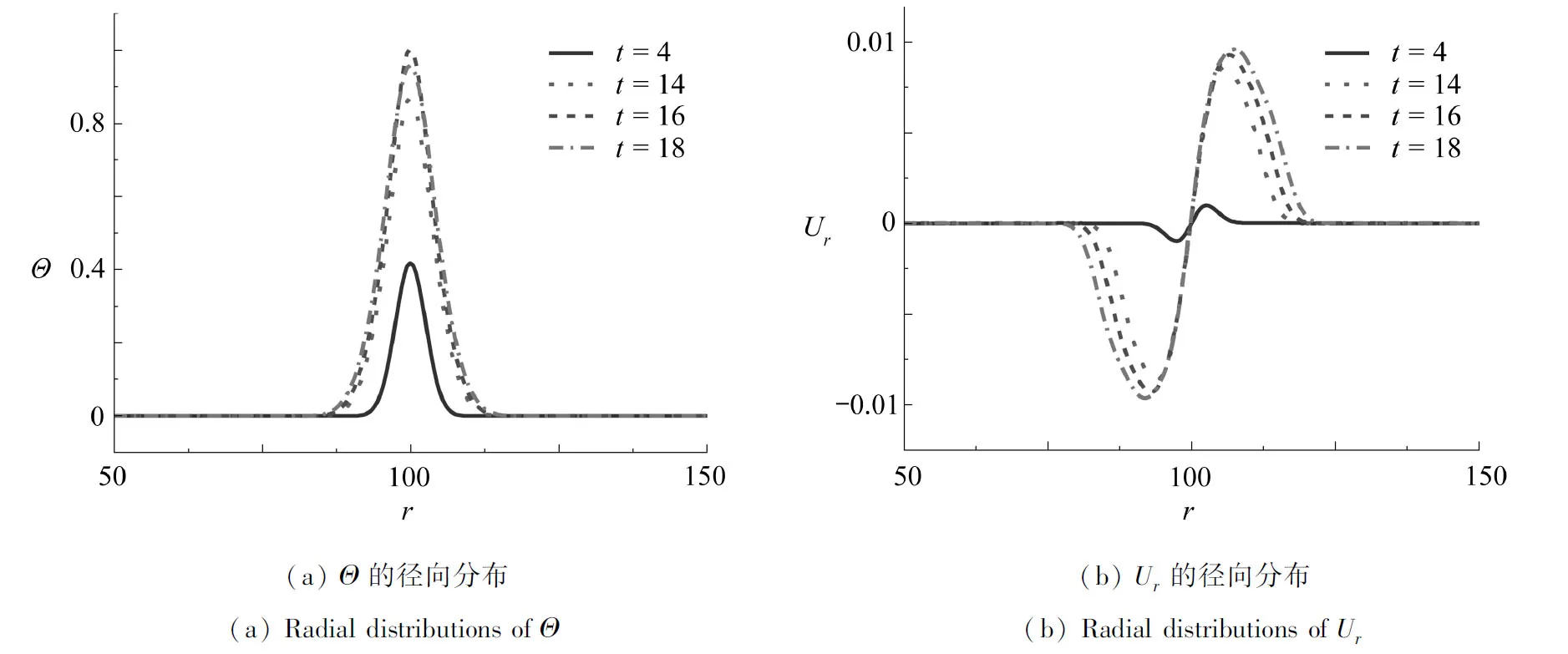
图5 脉宽为2时的热力响应Fig. 5 Thermal-mechanical responses with a pulse width of 2

脉宽为4时,z=5处的温度和应力分布曲线如图6所示．与脉宽为2时相似,t=16为热源刚消失的时刻,t=18为下一次热源刚出现的时刻．由图6(a)知,由于加热时间间隔减小,在两次加热之间的温度响应没有明显降低;而图6(b)、6(c)压应力峰值(r=100处)均随着时间的推移(热源的消失及出现)呈先增大后减小的变化．由于热机耦合,温度变化引起的弹性波会影响变形,导致应力发生变化,应力响应对热源的消失重现更为敏感．

在保证输入热量和加热时长不变(时长为10)的条件下,相同周期不同脉宽对z=5处物理量分布的影响如图7(a)—7(d)所示．由图7(a)可知,输入相同热量的情况下由于所需时间较长,脉宽越短的热影响区内可达到的温度峰值越低;由图7(b)可知,脉宽越长位移峰值越大．同时,由于脉宽为2(较短)时脉冲次数增大(总加热时长不变,非加热时间变长),会导致位移分布曲线在下降时出现“台阶”．研究参数变化对应力分布的影响,可以发现脉宽变短会导致径向应力σrr和周向应力σθθ显著减小,且由于脉冲间隔变大导致应力出现更多的峰值．

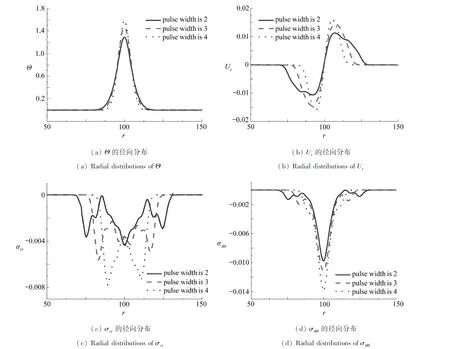
图7 不同参数下的热力响应Fig. 7 Thermal-mechanical responses under different parameters

2.3 比热容随温度变化

已有研究发现,由于非金属主要通过晶格振动实现导热,其导热形式分为声子导热和光子导热两种．温度较低时声子导热占主导,温度较高时光子导热占主导,比热容会随温度变化[32-33]．考虑材料比热容随温度变化,可将比热容写作无量纲温度的函数：

cE=c1(a+φ(Θ))．

(19)

修改式(8)中的无量纲参数η0为

(20)

重新改写无量纲温度控制方程可得

(21)

若式(19)中a+φ(Θ)=1,则式(21)退化为比热容为常数时的无量纲控制方程．

根据单水维[34]测量的结果,YSZ的比热容随温度的变化可表示为如下拟合形式：

(22)

对热松弛时间重新进行无量纲化处理可得

(23)

当cE随温度变化时,考虑到a+φ(Θ)变化很小,对热松弛时间的影响较小,可取a+φ(Θ)=1.328,得到τ=1.574．

因此,为获得脉冲激光作用下YSZ响应的准确预测,需考虑比热容随温度变化对热力响应的影响,其余参数同上、仍保持为常数．为了更显著地体现比热容随温度的变化,取脉宽为3时不同物理量的对比结果如图8(a)—8(d)所示．

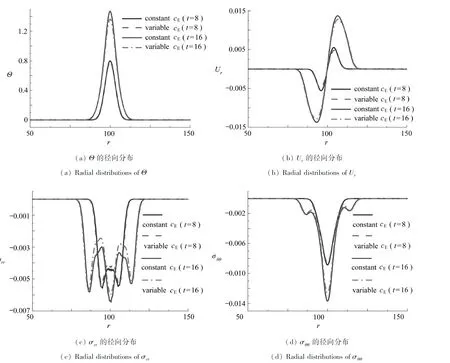
图8 比热容是否变化对热力响应的影响Fig. 8 Effects of the specific heat capacity change on the thermal-mechanical response

脉宽为3时,t=8和11分别为加热及不加热的时刻．由图8(a)可知,当比热容随温度变化时,相同的加热条件下温度峰值更低;从图8(b)中可知,比热容的变化会使得位移曲线整体降低(位移减小)．由应力分布曲线可知比热容随温度变化会导致径向正应力σrr和周向正应力σθθ分布曲线的绝对值低于比热容为常数时的情况．

2.4 波的反射

机械波会传播至材料底端并发生反射,进而对已经受到脉冲作用区域的热力响应造成影响．为观察具体的传播情况,计算域大小保持不变,纵向上热源仅在z>5的区域作用,单次作用的无量纲时间为10,其他条件与2.2小节中保持一致．计算得到不同时刻应力的云图分布与z=10上的应力分布曲线,如图9—11所示．

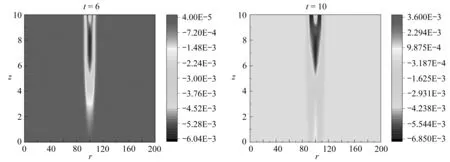
图9 应力σrr随时间的变化Fig. 9 Variations of stress σrrwith time

由σrr云图随时间的变化可知,在径向的压应力会随着时间的推移逐渐分离成两个独立的部分分别向圆心和远离圆心的方向传播．同时,σrr在纵向上经反射后形成的拉应力波反作用于热源位置处,并最终形成拉压交替的应力波在径向上传播．由σθθ云图随时间的变化及表面处σθθ的径向分布可知,由压应力波反射后产生的拉应力波会沿压应力波的两侧传播,直到反作用于计算域的上端,在热源的周围形成拉应力,且热源外侧的拉应力更为显著．

图10 应力σθθ随时间的变化Fig. 10 Variations of stress σθθ with time

图11 z=10处的应力分布Fig. 11 Stress distributions at z=10

3 结 论

本文基于L-S广义热弹性理论、计及材料比热容随温度变化建立了激光脉冲作用下的热弹控制方程,利用有限元方法研究了YSZ在受到多次热冲击下的热力响应．通过分析得到了以下结论：

1) 随着脉冲作用次数的增加,σrr,σθθ均出现多个峰值;除位移值随着时间一直增加外,温度、应力的响应均随着脉冲产生周期性变化,而应力响应对脉冲的消失重现更加敏感．

2) 在输入能量保持不变的情况下,脉宽越短,由于热量耗散导致温度、位移、应力的响应峰值越小．

3) 考虑材料比热容随温度变化,温度、位移和应力响应均降低,表明考虑比热容与温度的相关性对响应的准确预测至关重要．

4) 周向应力σθθ在边界处的反射会在热源两侧产生拉应力,且外侧更为显著;径向应力σrr在传播中沿径向上发生分离,受反射波的作用最终形成拉压交替的应力波．随应力波的传播,材料则受到拉压交替的疲劳载荷作用．