一维六方压电准晶双材料界面共线裂纹问题

卢绍楠, 赵雪芬, 马园园

(1. 宁夏大学 数学统计学院, 银川 750021;2. 宁夏大学新华学院, 银川 750021)

0 引 言

1982年发现的准晶具有宏观对称性和结构上的完全有序性[1]．常温下准晶呈脆性, 其对裂纹、孔洞、位错等缺陷非常敏感[2]．为了使准晶材料被充分利用, 研究裂纹、位错等缺陷具有一定的意义．在考虑表/界面效应下, 苏梦雨等[3]分析了纳米尺度下一维六方准晶中含有椭圆形裂纹孔的Ⅲ型断裂问题; Cheng等[4]研究了一维六方准晶矩形板在有限维度下的断裂问题; 利用复变函数方法和Stroh公式, 张炳彩等[5]研究了一维六方准晶中孔边不对称共线界面裂纹问题．借助边值问题, Su等[6]研究了一维六方准晶中纳米椭圆孔边裂纹的Ⅲ型断裂问题．利用广义Stroh公式, Radi等[7]求解了二维十次对称准晶直线裂纹问题．通过构造广义保角映射, 高媛媛等[8]研究了一维正交准晶中具有穿透性的椭圆孔口的平面弹性问题．

压电准晶相较普通的压电材料而言具有更广阔的应用前景．基于保角映射技术, 在部分渗透边界条件下, Yang等[9]讨论了一维六方压电准晶中带两个非对称裂纹椭圆孔的断裂问题．Hu等[10]研究了不同准晶材料之间的界面裂纹问题．运用Fourier积分变化, Zhou和Li[11-12]分别研究了有限厚度一维六方压电准晶板中币形裂纹和Yoffe型运动裂纹问题．利用Schwarz-Christoffel变换, 刘兴伟等[13]研究了一维六方压电准晶中正n边形孔边裂纹问题．

由两种材质不同的准晶材料沿界面结合在一起, 称为“准晶双材料”．目前, 关于准晶双材料界面断裂问题的研究多采用积分方程方法, 得到的是数值解, 外载荷多为均匀分布．集中载荷作用下压电准晶双材料界面多裂纹问题的研究还未有文献报道．基于此, 本文利用复变函数方法求解了集中载荷(力和电荷)作用下压电准晶双材料界面共线裂纹反平面问题, 得到了形式简洁的裂纹尖端场强度因子(包含声子场、相位子场应力强度因子和电位移强度因子)的解析解．解析解严谨性更强,且在工程计算中更加便捷, 同时解析解对于理解物理现象和本质具有重要的作用和意义．

1 一维六方压电准晶基本公式

取z1轴为一维六方压电准晶准周期方向,xOy面为其周期平面, 建立直角坐标系．此时, 一维六方压电准晶反平面弹性平衡方程为[14]

∇2uz1=0, ∇2wz1=0, ∇2v=0．

(1)

其通解为[15]

uz1=Reφ(z),wz1=Reψ(z),v=Reη(z)．

(2)

应力分量表示为[14]

(3)

2 一维六方压电准晶双材料反平面弹性问题

如图1所示, 上下平面分别为弹性常数不同的一维六方压电准晶材料, 记上半平面为S+,下半平面为S-．上下半平面的量分别用上标1和2标记．设反平面集中力P(假设作用在声子场的力为P1,作用在相位子场的力为P2)和电荷Q集中作用在S+内任意点z0处．这里沿实轴的区间L=L1+L2+…+Ln,Lj上两种一维六方压电准晶材料完全黏合, 应力和位移保持连续, 即

图1 集中载荷作用于含共线界面裂纹的一维六方压电准晶双材料Fig. 1 A 1D hexagonal piezoelectric quasicrystal bimaterial with collinear interfacial cracks under a concentrated load

(4)

(5)

沿界面其余部分L′=L′1+L′2+…+L′n互相裂开, 其中L′i表示第i条有限长裂纹．假设在裂纹上无面力作用, 裂纹端点依次是a1,b1;a2,b2;…;an,bn,

(6)

3 集中载荷作用下一维六方压电准晶双材料界面共线裂纹反平面弹性问题求解

如图1, 由式(2), 在S+内, 设

(7)

式中,M1,M2,M3的表达式见附录,φ10(z),ψ10(z)和η10(z)在S+内全纯．

在S-内无集中作用载荷, 可设

(8)

这里,φ2(z),ψ2(z)和η2(z)在S-内全纯．

由Schwarz对称原理[16], 对φ′1(z),ψ′1(z),η′1(z)和φ′2(z),ψ′2(z),η′2(z)做如下的延拓：

(9)

将式(7)代入式(9)得到

(10)

式中,φ10(z),ψ10(z)和η10(z)在沿L隔开的全平面全纯,

(11)

在S-内无外载荷作用, 故φ′2(z),ψ′2(z)和η′2(z)在S-内全纯, 做如式(10)的解析延拓可知,φ′2(z),ψ′2(z)和η′2(z)在沿L割开的全平面全纯．

注意到式(4)和式(6), 下式成立：

因此有

(12)

其中,t属于全实轴．

根据推广的Liouville定理[17], 并考虑式(9)和式(10)有

(13)

这里,z属于全平面,D0,D1,D2为待定常数．

由位移连续条件, 可得

(14)

其中,N1,N2,N3,D3,D4,D5的表达式见附录．

式(14)的积分形式解为

(15)

其中

(16)

X0(z)是沿L割开的z平面上的单值分支, 满足

(17)

(18)

计算式(15)中的积分后, 得到

(19)

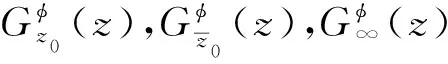
在φ′2(z),ψ′2(z)和η′2(z)中,有c0,c1,…,cn,d0,d1,…,dn,f0,f1,…,fn,D3,D4和D5共3(n+2)个常数需要确定, 这就需要3(n+2)个方程．根据无穷远处的受力情况, 可得到6个常数; 其余3n个方程由位移单值条件导出．式(13)仅利用了L两边(S+与S-)声子场和相位子场位移的导数相等．另外还需补充在n个裂纹端点处位移相等的条件以满足L上两边位移相等．由各裂纹两端位移相等, 有

(20)

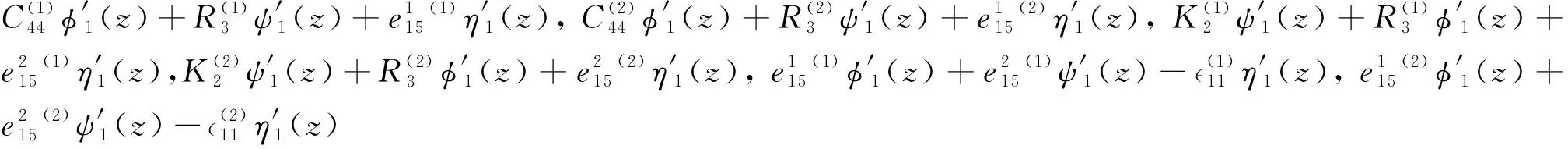
考虑式(13), 得

(21)

其中j=1,2,…,n．

4 特 例

φ′i(∞)=ψ′i(∞)=ηi′(∞)=0．

(22)

将式(22)代入式(13), 得到

D0=0,D1=0,D2=0,D3=0,D4=0,D5=0．

(23)

由式(15)和式(22),可得

c0=d0=f0=0．

(24)

4.1 一条有限长界面裂纹

如图2所示, 设界面上有一条从a到b的裂纹, 在S+内任意点z0处作用集中载荷．此时n=1,则

图2 集中载荷作用在含一条界面裂纹的压电准晶双材料Fig. 2 A piezoelectric quasicrystal bimaterial with an interfacial crack subjected to a concentrated load

Pn(z)=c1,Qn(z)=d1,Fn(z)=f1,

(25)

(26)

(27)

(28)

(29)

下面确定常数c1和d1,由式(21)和式(23)可得

(30)

考虑围道积分, 由留数定理得

c1=N1,d1=N2,f1=N3．

(31)

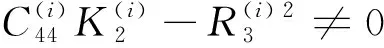
(32)

其中,B1,B2,B3,E1,E2,E3,G1,G2,G3的表达式见附录．

4.2 两条有限长界面裂纹

如图3所示, 设界面上有两条等长的裂纹, 裂纹端点依次为-b,-a,a,b,在S+内任意点z0处作用集中载荷．当n=2时,

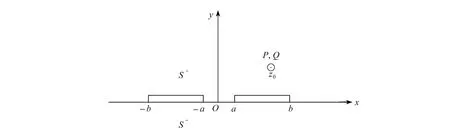
图3 集中载荷作用在含两条界面裂纹的压电准晶双材料Fig. 3 A piezoelectric quasicrystal bimaterial with 2 interfacial cracks subjected to a concentrated load

Pn(z)=c1z+c2,Qn(z)=d1z+d2,Fn(z)=f1z+f2,

(33)

(34)

(35)

(36)

(37)

(38)

(39)

5 裂纹尖端场强度因子

计算双材料界面裂纹Ⅲ型场强度因子[18]：

(40)

5.1 一条界面裂纹

1) 任意位置受集中载荷

如图2, 将式(19)和式(31)代入式(40)得

(41)

其中I1,I2,I3,J,L1,L2,L3的表达式见附录．

2) 裂纹面上受集中载荷作用

如图4所示, 当z0→t,t为上半平面上任意点时, 由式(41)可得

(42)

令t→0,由式(42)可得

(43)

3) 裂纹面上受均布集中载荷

如图5所示, 在上半平面裂纹面上, 任意区段(a,b)受均布集中载荷作用, 由式(42)积分得

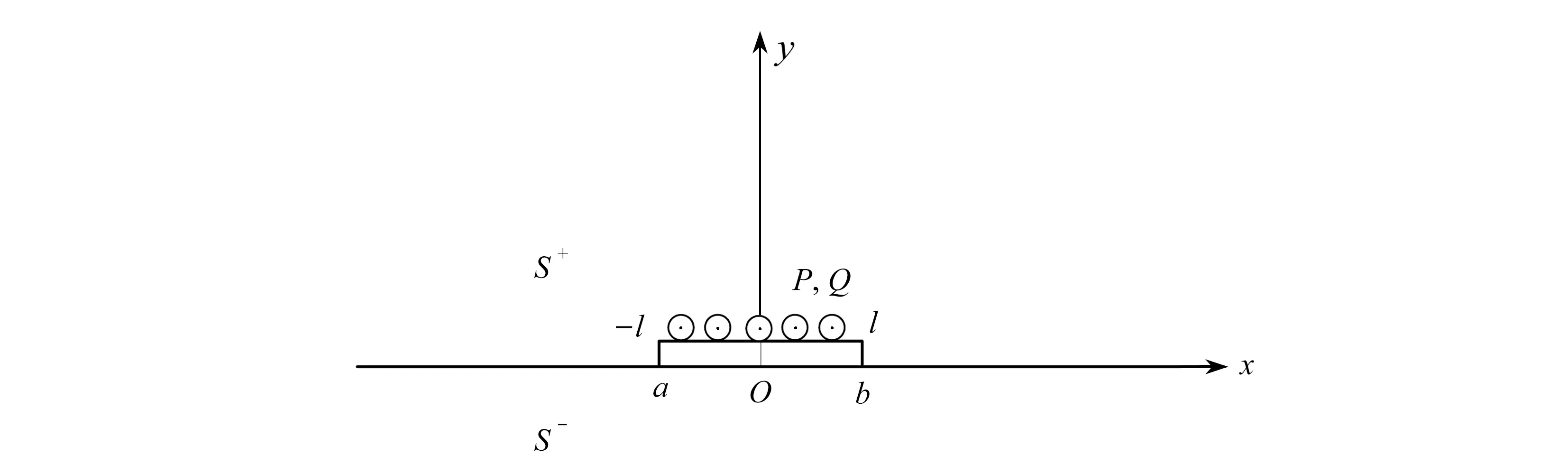
图5 单个界面裂纹面上受均布集中载荷Fig. 5 A single interfacial crack surface subjected to uniformly distributed concentrated loads

(44)

当a=-l,b=l,载荷布满裂纹面时,

(45)

5.2 两条界面裂纹

1) 任意位置z0受集中载荷作用

结合两条有限长界面裂纹的情形, 将式(19)代入式(40), 并考虑到式(38), 在裂纹尖端x=a处

(46)

其中

在裂纹尖端x=b处

(47)

其中

2) 裂纹面上受集中载荷作用

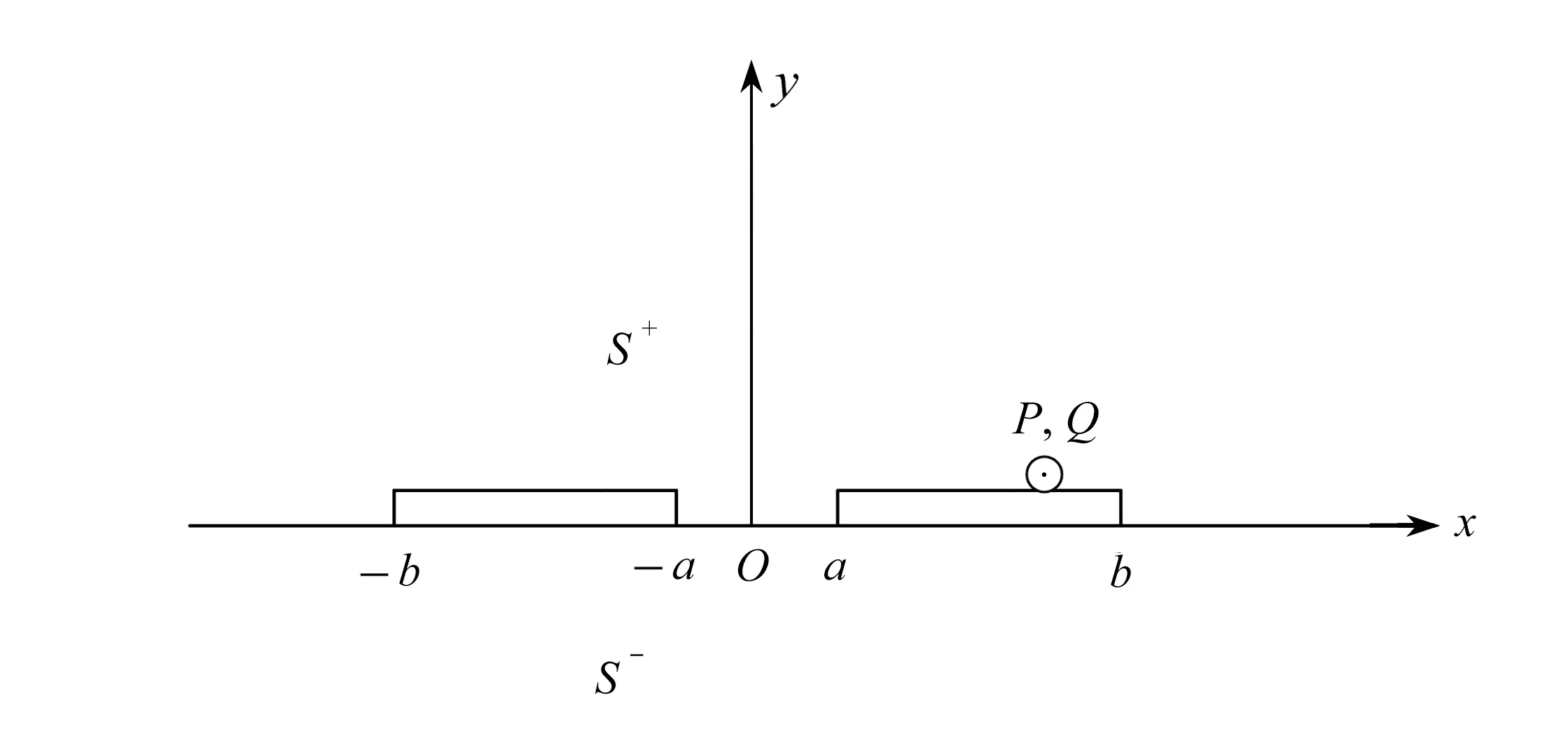
图6 集中载荷作用在界面裂纹面Fig. 6 A concentrated load applied to the interface crack surface

(48)

式中

在裂纹尖端x=b处, 令z0→t,得

(49)

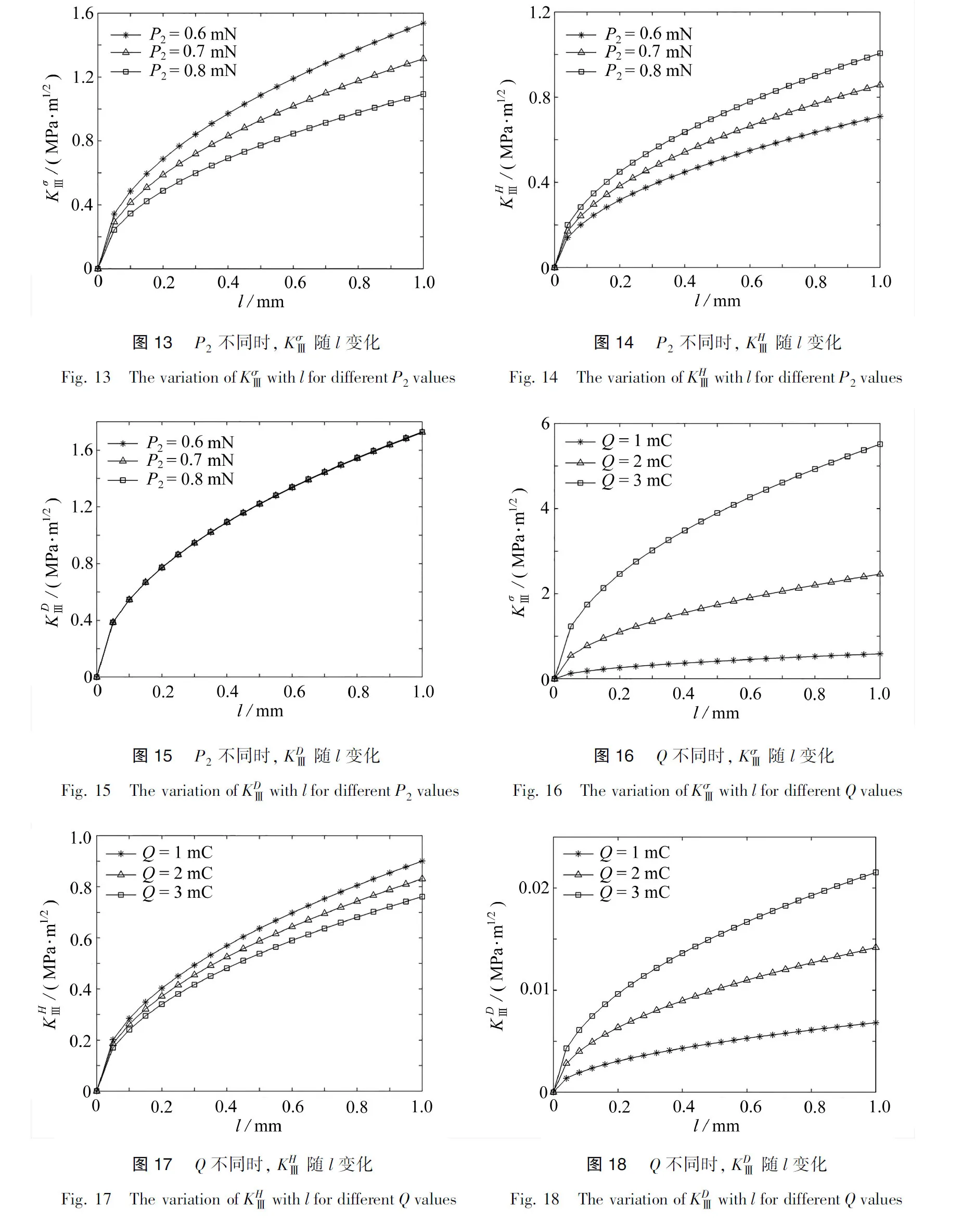
6 数 值 算 例

从式(49)中可以看出, 裂纹尖端场强度因子与弹性常数、外载荷以及裂纹长度的取值有关．数值算例分别讨论集中力和电荷、双材料耦合系数之比不同时,场强度因子随裂纹长度的变化规律．本节仅讨论一条界面裂纹受反平面集中载荷作用下的情形．一维六方压电准晶双材料弹性常数如表1所示[19]．

表1 一维六方压电准晶双材料弹性常数

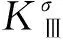
7 结 论

本文研究了一维六方压电准晶双材料在集中载荷(力和电荷)作用下共线裂纹的反平面弹性问题．基于复变函数理论, 把弹性问题转化为解析函数边值问题进行求解, 得到了裂纹尖端场强度因子的解析解．作为特例, 给出了不同载荷作用下含有一条和两条界面裂纹的封闭解．数值算例分析了场强度因子随裂纹长度、外载荷以及双材料耦合系数之比改变时的变化趋势．

致谢本文作者衷心感谢宁夏大学新华学院科学研究基金项目重点项目(23XHKY01)对本文的资助．

附 录

① 式(7)中的M1,M2,M3表达式如下：

(A1)

其中

② 式(14)中的N1,N2,N3,D3,D4,D5表达式如下：

(A2)

(A3)

其中

③ 式(32)中的B1,B2,B3,E1,E2,E3,G1,G2,G3表达式如下：

(A4)

(A5)

(A6)

④ 式(41)中的J,I1,I2,I3,L1,L2,L3表达式如下：

(A7)

(A8a)

(A8b)

(A8c)