表达式转换及求值探析

(1、2.安顺学院电子与信息工程学院，贵州 安顺561000)

0 引言

表达式是由操作数、运算符和界限符组成。操作数可以是常数、变量、表达式，运算符可以是算术运算符、关系运算符和逻辑运算符，界限符有左右括弧和表达式结束符。表达式有中缀、前缀和后缀表示法。中缀表达式(通常称表达式)，是运算符放在两操作数的中间，如：a+b、4*3/(4-2)+8，它是表达式的常见表示法。前缀表达式是运算符放在两操作数的前面，如：+ab、+/*43-428。后缀表达式是运算符放在两操作数的后面，如：ab+、43*42-/8+。

表达式求值是数学中的一个基本问题，也是程序设计中的一个常见问题。对于表达式的三种表示法，计算机可以采用不同的运算规则来求解。表达式的运算规则：先乘除，后加减，从左到右计算，先括号内，后括号外，即表达式运算不仅要依赖运算符优先级，还要处理括号，在计算机中操作很不方便。前缀表达式的运算规则：连续出现的两个操作数和在它之前出现且紧靠它的两个操作数构成一个最小表达式。后缀表达式的运算规则：每个运算符和在它之前出现且紧靠它的两个操作数构成一个最小表达式。由此可见，后缀表达式中运算符出现的顺序正是表达式的运算顺序。因此，在对表达式求值时，通常先将表达式转换成相应的后缀表达式，再对后缀表达式进行求值。

1 表达式转换研究现状

目前，表达式之间的转换已有很多研究。如：文献[1]介绍了利用两个栈及括号法实现表达式转换为后缀表达式的方法，但对括号转换法的描述：“移动所有运算符来取代所有的右括号，并以最近为原则进行替换。”，容易把运算符和右括号对错位；文献[2]介绍了利用栈和数组实现表达式转换为后缀表达式的方法；文献[3]和[7]介绍了利用二叉树实现表达式转换为后缀表达式的方法，但对转换过程的描述不够清楚；文献[5]介绍了用两个栈、加括号及语法树实现表达式转换为后缀表达式的方法，但文中对括号转换法的描述：“将每个运算符移到其所在括号的外面。”，没有说明清楚运算符是移到括号的前面还是后面，容易产生歧义。因为运算符移到其所在的括号前面和后面得到的是表达式不同的表示形式；文献[6]和[9]介绍了用一个栈实现表达式转换成后缀表达式的方法；文献[10]、[11]及[12]介绍了利用两个栈实现中缀表达式转换后缀表达式方法及后缀表达式的求值。

通过分析、对比目前表达式转换成后缀表达式的各种方法，总结得出目前表达式转换为后缀表达式的方法主要有：(1)利用两个栈进行转换；(2)利用一个栈进行转换；(3)利用二叉树进行转换；(4)用(加)括号法进行转换。但这些转换方法不够全面和完整，本文提出了这几种转换方法：(1)利用栈和队列进行转换；(2)加括号去括号进行转换；(3)直接转换；(4)二叉树进行转换。以期对表达式转换为后缀表达式的方法进行补充和完善。

2 表达式转换成后缀表达式的方法

2.1 利用栈和队列进行转换

将一个表达式(exp)转换成后缀表达式，操作数之间的相对次序不变，但运算符的相对次序可能要变，同时还要去掉括号。文章根据表达式中运算符优先级、结合栈及队列的特点，利用一个顺序栈和一个顺序队列来实现表达式转换为后缀表达式，其中顺序栈S存储运算符，顺序队列Q存储中间结果，其具体转换过程的伪代码描述如下：

InitStack(S);

InitQueue(Q);

While(从exp读取字符ch,ch!=’’)

{ If(ch为数字)

enQueue(Q,ch);

If(ch为运算符)//比较ch与S栈顶运算符的优先级;

{ if((S为空)or (栈顶运算符为左括号’(‘)

push(S,ch)；

if(S不空)

{ if(ch优先级高于栈顶运算符)

push(S,ch)；

Else

{Pop(S,e);

enQueue(Q,ch);}

}

}

If(ch为括号)

{ If(ch==’(‘)

push(S,ch)；

Else

{ Pop(S,e);

while(e!=’(‘)

{enQueue(Q,e);

Pop(S,e);}

}

}

}

While(!StackEmpty(S))

{Pop(S,e)；

enQueue(Q,ch)；}

While(!QueueEmpty(Q))

{deQueue(Q,e);

Printf(“后缀表达式为%c”,e);

}

例：将表达式4*3/(4-2)+8转换成后缀表达式，利用栈S和队列Q进行转换，其转换过程中栈S和队列Q的变换如表1所示：

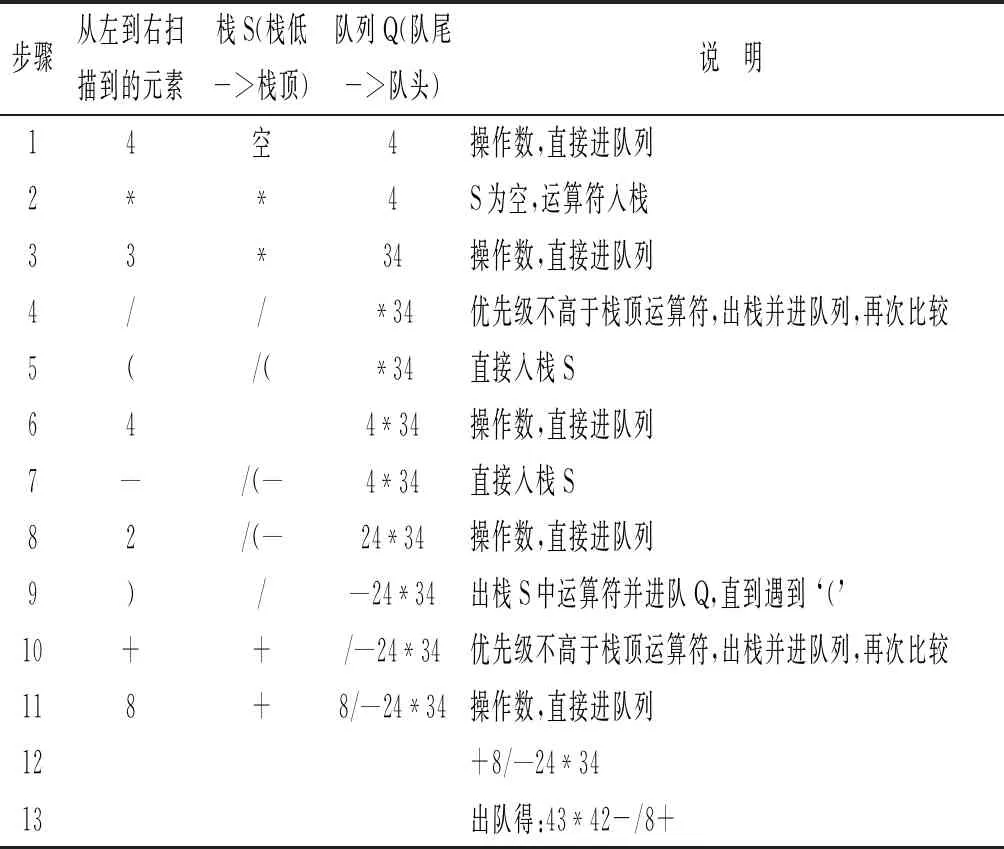
表1 表达式4*3/(4-2)+8转换成后缀表达式的过程

2.2 利用二叉树进行转换

本文再次提出利用二叉树进行表达式转换为后缀表达式，主要是基于之前的研究对转换过程描述不够清楚。在此，对该转换法进行补充和完善。基于表达式和二叉树递归定义的相似性，在把表达式转换为二叉树时，把操作数作为叶子节点，操作符作为非叶子节点。其转换步骤如下：

(1) 将表达式转换为二叉树；

将表达式按照优先级为每个运算式加上括号，从最外层括号开始对每对括号内的表达式进行转换：运算符为根节点，第一个表达式为左子树，第二个表达式为右子树，直至转换完毕。

(2)对二叉树进行后序遍历即得表达式对应的后缀表达式。

例：将表达式4*3/(4-2)+8转换成后缀表达式。其具体转换过程如下：

(1)将表达式4*3/(4-2)+8转换为对应的二叉树

(1-1)按照优先级加上括号，得到：(((4*3)/(4-2))+8)

(1-2)从最外层括号开始，对每对括号内的表达式进行转换：

(1-2-1)运算符“+”为根节点 ，第一个操作数“((4*3)/(4-2))”为左子树T1，第二个操作数“8”位右子树T2；

(1-2-2)再对左子树T1中再进行转换，“/”为T1的根节点，“(4*3)”为T1左孩子T11，(4-2)为左子树T1的右孩子T12；

(1-2-3)对T11进行转换，“*”为T11的根，“4”位T11左子树T111 ，“3”为T11右子树T112；

(1-2-4)再对T12进行转换，“-”的为T12的根，“4”为T12左子树T121，“2”为T12的右子树T122；

(2)对二叉树进行后序遍历

由上述转换过程得到表达式对应的二叉树如下图1所示，再对二叉树进行后续遍历得对应后缀表达式“43*42-/8+”。

另，在得到表达式对应的二叉树后，若要求表达式对应的前缀表达式，只需对二叉树进行前序遍历即可。

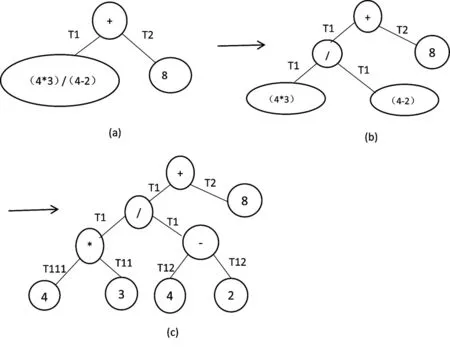
图1 表达式对应的二叉树

2.3 利用加括号去括号法进行转换

在求表达式的后缀表达式时，利用栈和队列进行转换及利用二叉树进行转换两种方法比较常用，尤其是在算法分析设计方面。而在学习、生活中，会遇到一些只要求写出表达式对应的后缀表达式，而不需要写算法的选择题、填空题。如：美团曾经出过的一个笔试选择题目：中缀表达式X=A+B*(C-(D+F))/E转后缀表达之后是什么？答案为A.ABCDF+-*E/+; B.ABDF+C-*E/+; C.ABDF+C*-E/+;D.ABDF+C*-E+/；北京邮电大学2006年“算法与数据结构”考研题：写出表达式23+((12*3-2)/4+34*5/7)+108/9的后缀表达式；吉林大学2007年“算法与数据结构”考研题：将表达式(a+b)*c+d-(e+g)*h改写成后缀表达式。此时，若用前面两种转换法，相对费时。在此，提出一种快速而简单的转换方法：加括号去括号法，这种方法可以直接快速地求出表达式的后缀表达式。其基本步骤如下：

(1) 依据“先乘除后加减、先括号内后括号外”的原则确定表达式的运算顺序，对所有的运算单位加括号；

(2) 将每个运算符移到其所在括号的后面；

(3) 去除表达式中所有括号既得到相应的后缀表达式。

例:将表达式4*3/(4-2)+8转换成后缀表达式，其转换过程如下：

(1) 按优先级别，将每一步要计算的表达式加上括号：

(1-1)(4*3)/(4-2)+8

(1-2)((4*3)/(4-2))+8

(1-3)(((4*3)/(4-2))+8)

(2) 将每个运算符移到其所在括号的后面:

(2-1)(((4*3)/(4-2))8)+

(2-2)(((4*3)(4-2))/8)+

(2-3)(((43)*(4-2))/8)+

(2-4)(((43)*(42)-)/8)+

(3)去除表达式中所有括号既得到相应的后缀表达式：

43*42-/8+ 。

利用加括号去括号法，不难快速得出中缀表达式X=A+B*(C-(D+F))/E转后缀表达之后是C答案(即：ABDF+C*-E/+)；表达式23+((12*3-2)/4+34*5/7)+108/9的后缀表达式是23.12.3*2-4/34.5*7/++108.9/+(表达式中的点(.)是数分隔符)；表达式(a+b)*c+d-(e+g)*h改写成后缀表达式是ab+c*d+eg+h*-。

另，若将此方法推广到求表达式的前缀表达式时，只需把(2)中的每个运算符移到其所在括号的前面即可，其他步骤一样。

2.4 直接转换

这里，介绍一种更快速的表达式转换为后缀表达式的方法，称直接转换法，直接转换法实质上是对“加括号去括号法”的进一步优化，即：在表达式中不用加括号，直接把每个运算符移到其所对应的操作数之后，并去掉原表达式中的括号。具体转换步骤为：(1)从左到右，把每个运算符移到它所对应的两个操作数之后；(2)去掉表达式中所有括号。

例:将表达式4*3/(4-2)+8转换成后缀表达式。

(1) 把从左到右，把每一个运算符放在它所对应的两个操作数之后：

(1-1) 43*/(4-2)+8

(1-2) 43*(4-2)/+8

(1-3) 43*(42)-/+8

(1-4) 43*(42)-/8+

(2) 去掉表达式中所有括号:

43*42-/8+

直接转换法和加括号去括号法转换方法一样，用于快速解出填空、选择题的答案。若将此方法用于表达式缀转换为前缀表达式时，只需(1)中把每个运算符移到其所对应的操作数之前即可，其他步骤一样。

3 表达式求值

在计算机中进行表达式求值时，根据表达式三种表示形式的不同特点，通常先将表达式转换为后缀表达式,再对后缀表达式进行求值，具体过程如下： InitStack(S);；

While(从exp读取字符ch,ch!=’’)

{

If(ch为数字)

push(S,ch)；

If(ch为运算符op)

{

Pop(S,a);

Pop(S,b);

push(S,(b op a));

}

}

Pop(S,e);//e即为表达式的值

例：求表达式4*3/(4-2)+8的值。其求值过程如下：

(1) 利用上述任何一种方法求得表达式4*3/(4-2)+8的后缀表达式为43*42-/8+；

(2) 对后缀表达式求值过程如下表2所示，最后栈中元素14，出栈即得表达式结果14。

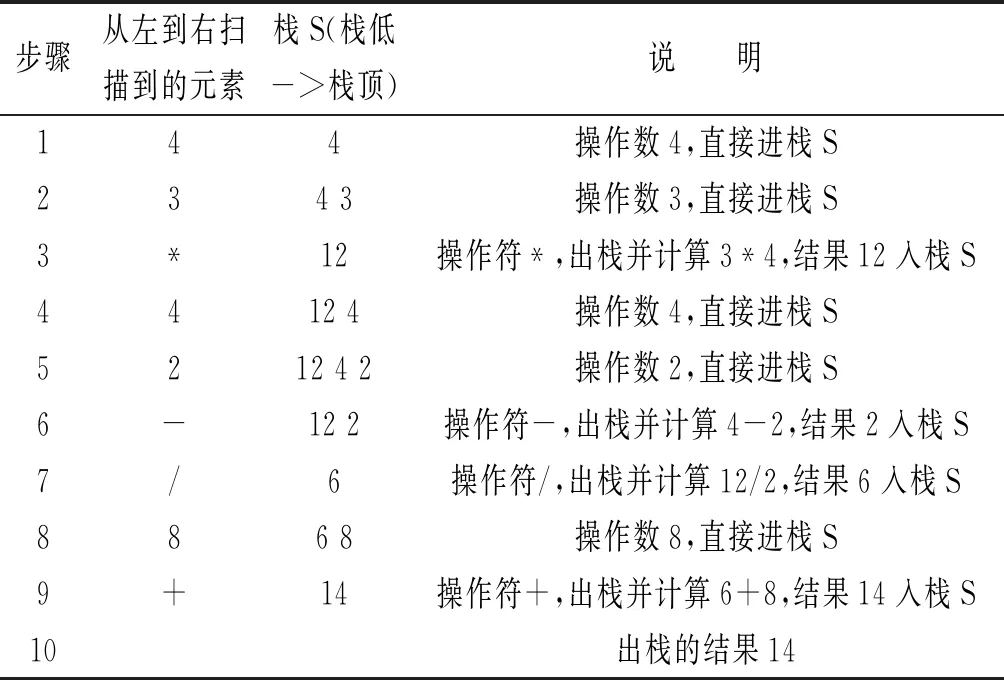
表2 后缀表达式43*42-/8+的求值过程

结 语

本文介绍的四种表达式转换成后缀表达式的方法，对已有的转换法进行了很好的补充和完善。每种方法都有各自的特点，在实际应用中，最重要的是要先分析问题，根据问题的不同要求选择不同解决方法。如；只求表达式的后缀表达式，不要求写算法，可选用加括号去括号法或直接转换法；如果要求转换为后缀表达式并写算法，则选用利用栈和队列进行转换较好；如果同时求表达式的前缀表达式和后缀表达式，则选用利用二叉树进行转换法较为合适。