二叉树创建方法

陈文

（福州职业技术学院，福州 350108）

0 引言

二叉树是《数据结构与算法》课程的重要内容，它是典型的树型数据结构[1]，二叉树的结构及二叉树的算法已广泛应用各类程序设计中[2-3]。分析研究二叉树的应用，首先要基于二叉树已经创建的前提下进行。因此，二叉树的创建则是一切二叉树算法应用的基础。然而，《数据结构与算法》的教材中，往往注重介绍二叉树的遍历方法及二叉树应用等，对二叉树的创建并未给出详细的分析。由于二叉树的遍历算法是基于二叉树已经创建的前提下，而本文所介绍的二叉树创建方法，却要用到二叉树的遍历等递归思想，因此，本文所介绍的二叉树创建方法是学完二叉树遍历等相关理论后，反过来进一步总结与分析二叉树的创建思想。它是对《数据结构与算法》教材的必要说明与补充。

本文着重介绍二叉树的创建方法，阐述二叉树创建的递归原理及二叉树创建的程序框架。并结合样例验证其正确性。同时，对学习二叉树的其他算法具有辅助作用。

1 直接递归创建二叉树

1.1 二叉树创建分析

以图1 所示的二叉树为例，二叉树的创建可用递归法创建。方法如图1。

图1 二叉树样例图

首先，创建根结点root，其值为a，再依次创建左子树及右子树。即输入序列如图2。

图2

二叉树的创建递归为根结点及左右子树的创建[4]。

为了使递归程序顺利执行，必须增加递归的出口条件。不妨以“#”字符表示为空结点作为出口条件，则二叉树可形象表示为图3。

图3 补充空结点后的二叉树

输入序列为图4。

图4

进一步转化为图5。

图5

完整的输入序列为：abd##eg##h##c#f##。

1.2 程序框架

本文利用C 语言程序设计描述结点的结构与程序框架，通过以上的分析可知：

结点结构：

二叉树创建的程序框架为：

1.3 程序运行结果

为验证所创建的二叉树正确性，可将其前序、中序、后序输出。二叉树前序、中序及后序的遍历方法有众多资料分析讨论[5]，常用的递归算法如下：

前序算法：

中序算法：

后序算法：

主程序：

运行结算如图6 所示。

图6 运行结果图

2 利用前序与中序的遍历结果，构造二叉树

2.1 二叉树与前序遍历的关系

二叉树与前序遍历结果存在多对一的关系。如二叉树1。

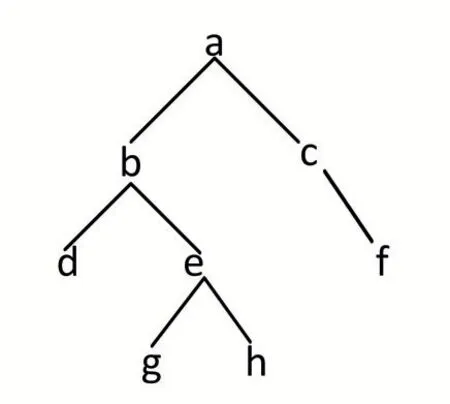
图7 二叉树1

与二叉树2。

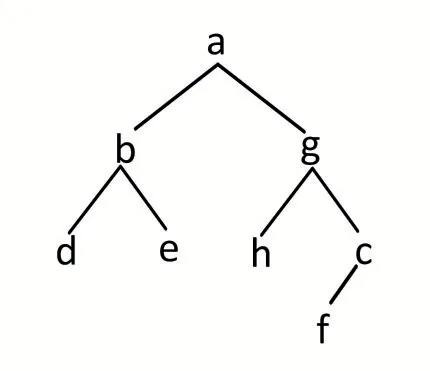
图8 二叉树2

前序遍历结果均为：abdeghcf。

由此可见，单从二叉树的前序遍历无法构建二叉树。

同样，单从二叉树的中序遍历或后序遍历也无法构建二叉树。

2.2 由前序及中序遍历结果构建二叉树

由前序及中序遍历结果可唯一确定二叉树。以图1 的二叉树为例，分析如下：

前序遍历abdeghcf。

中序遍历dbgehacf。

由前序遍历可知：a 为根结点。

再由中序遍历可知：左子树序列为dbgeh，右子树为序列为cf。

于是二叉树递归为图9。

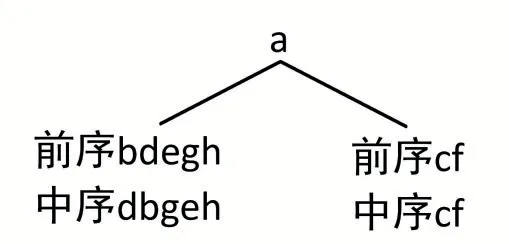
图9 递归分析图

递归的出口条件为前序或中序序列为空时，该二叉树为空树。

2.3 由前序及中序遍历结果构建二叉树的程序框架

形参说明：

predata[]、indata[]：前序及中序数组

pre1、in1：前序序列及中序序列起始位置

len：序列的长度

程序分析：

根结点字符为ch=predate[pre1]

ch 在中序中的位置loc=lookfor（indata，ch）

则：左子树序列长度llen=loc-in1

右子树序列长度rlen=len-llen-1

于是：前序序列predata 各位置元素如图10。

图10

中序序列indata 各位置元素如图11。程序框架：

图11

其中，函数lookfor（char*data，char ch）表示从数组data[]中查找字符ch，具体实现方法如下：

程序运行结果如上例中的图6 所示。

3 利用后序与中序的遍历结果，构造二叉树

程序的基本思想与“利用前序与中序的遍历结果，构造二叉树”相似。不再赘述。

4 结语

二叉树算法中普遍使用递归方法，本文提出二叉树的创建也是基于递归思想，因此，二叉树创建的研究探讨，有助于理解递归原理。将二叉树创建与二叉树其他算法相结合，有助于加深对二叉树的理解。同时，对提高二叉树的应用能力无疑具有积极意义。