倍增法之后缀数组解决重复子串的问题

周波 柳杰

【摘要】后缀数组是处理字符串的有力工具。利用后缀数组解决字符串问题，无论是在时间复杂度和空间复杂度上，都非常有优势，在信息学竞赛中也是非常实用的一个工具。本文分两部分，第一部分介绍倍增法构造后缀数组，第二部分介绍简洁高效代码的实现与应用。

【关键字】字符串 后缀 后缀数组 名次数组 快速排序

后缀数组的实现，本节主要介绍后缀数组的倍增法实现。

一、基本定义

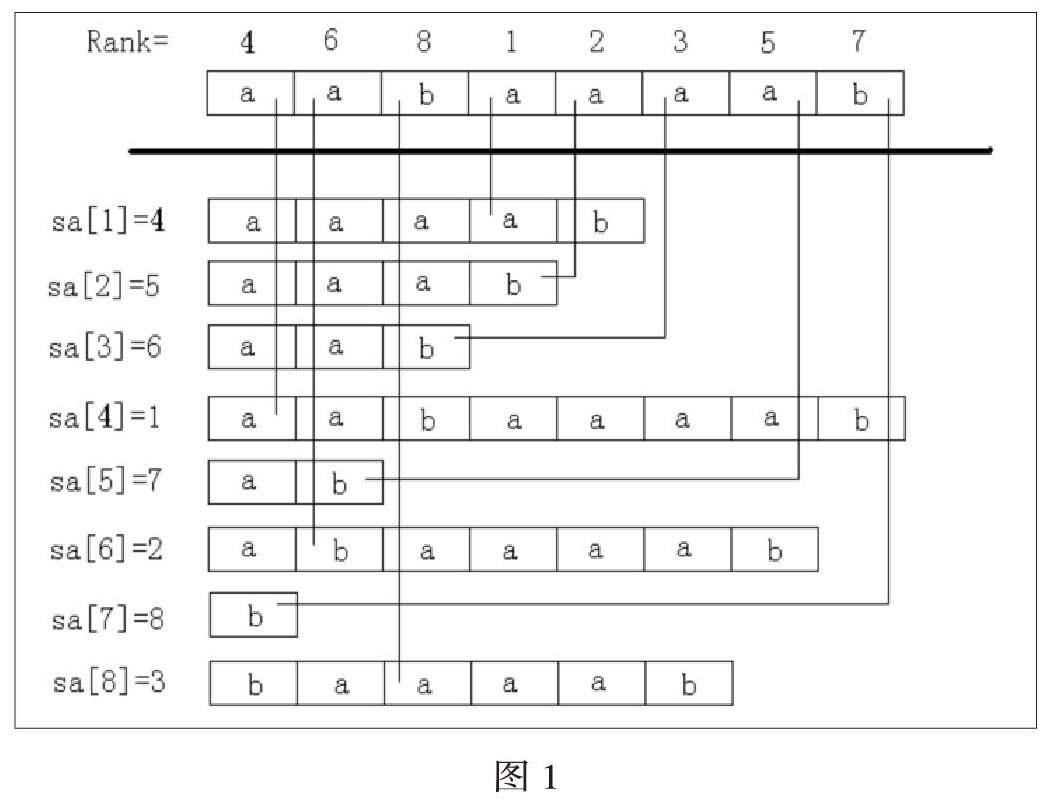
简单的说，后缀数组是“排第几的后缀串首字母在哪里？”，名次数组是“后缀串排第几？”。容易看出，后缀数组和名次数组为互逆运算。如图1所示。

设字符串的长度为n。为了方便比较大小，可以在字符串后面添加一个字符，这个字符没有在前面的字符中出现过，而且比前面的字符都要小。在求出名次数组后，可以仅用0（1）的时间比较任意两个后缀的大小。在求出后缀数组或名次数组中的其中一个以后，便可以用0㈤的时间求出另外一个。任意两个后缀如果直接比较大小，最多需要比较字符n次，也就是说最迟在比较第n个字符时一定能分出“胜负”。

二、倍增算法

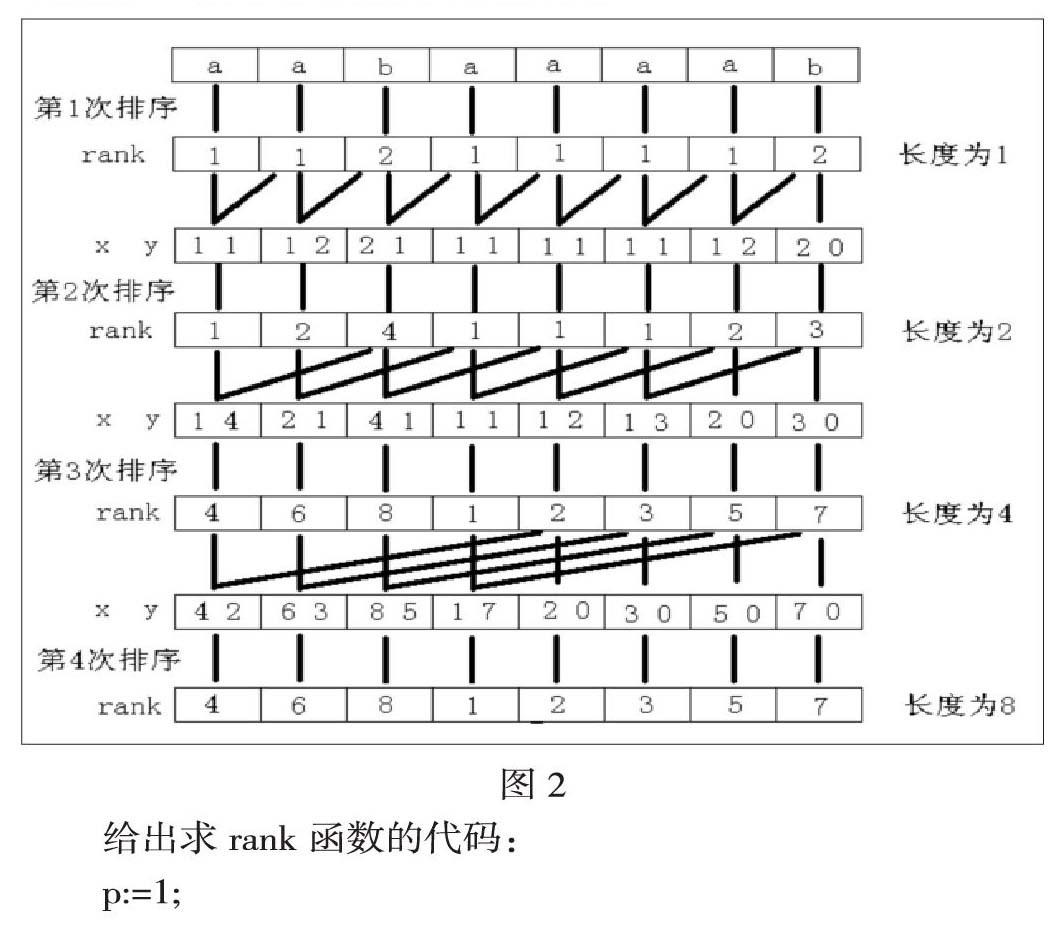
倍增算法的主要思路是：用倍增的方法对每个字符开始的长度为2k的子字符串进行排序，求出排名，即rank值。k从0开始，每次加1，当2k大于n以后，每个字符开始的长度为2k的子字符串便相当于所有的后缀。并且这些子字符串都一定已经比较出大小，即rank值中没有相同的值，那么此时的rank值就是最后的结果。每一次排序都利用上次长度的字符串的rank值，那么长度为2k的字符串就可以用两个长度为2k-1的字符串的排名作为关键字表示，然后进行排序，便得出了长度为2k的字符串的rank值。以字符串“aabaaaab”为例，整个过程如图2所示。其中x、y是表示长度为2k的字符串的两个关键字。