基于降阶模型和数据驱动的动态结构数字孪生方法

王青山, 严 波, 陈 岩, 邓 茂, 蔡源斌

(重庆大学 航空航天学院, 重庆 400044)

0 引 言

2003年Grieves首先提出了数字孪生概念[1],近年来其在各个领域受到广泛关注并成为研究热点[2-3]．数字孪生充分利用物理模型、传感器数据、运行历史数据等,在虚拟空间中完成映射,从而反映相对应的物理结构的全生命周期过程．数字孪生体跟随物理结构一同演化,可以实现物理结构状态实时智能监测和预测等．结构数字孪生方法的研究刚刚起步,其构建方法是重要的基础,具有非常广阔的应用前景．

近年来,已有关于结构数字孪生的研究报道．Haag和Anderl[4]给出了结构数字孪生的概念,并建立了一个弯曲梁试验平台以验证数字孪生概念,但没有给出建立数字孪生的具体过程．Moi等[5]用有限元模拟了一个小型转向节臂起重机的实时变形,基于应变传感器数据,利用逆方法建立了用于状态监测的数字孪生体．Wang等[6]结合数值仿真、传感器数据、多保真代理模型和可视化技术给出了建立数字孪生的方法,并利用桁架结构物理模型对方法进行了验证．Lai等[7]建立了起重机吊臂的三维有限元高保真模型和空间梁有限元低保真模型,进而建立了吊臂的多保真模型,构建了其数字孪生体以实现结构安全性监测．上述这些工作都没有考虑结构的损伤变化和所受载荷的动态惯性效应．Kapteyn等[8-9]提出了一种基于组件的降阶模型和机器学习算法构建数据驱动数字孪生的方法,给出了一固定翼无人机机翼数字孪生体的建立过程,考虑了机翼的损伤．Milanoski等[10]针对一个航空复合材料加筋板,结合有限元模拟和布拉格光栅传感器应变测量数据,建立了该加筋板的数字孪生体,其可预测结构所受静载荷和损伤位置．但文献[8-10]的工作没有考虑结构动力载荷的影响．

Wang等[11]针对一旋转轴,给出了其简化系统的空间梁参数有限元模型,提出了一种基于参数灵敏度分析的故障模型更新方案,建立了用于故障诊断的数字孪生模型,但对于复杂结构,用于敏感性分析的参数难以确定,难以实现模型的实时更新．Ganguli和Adhikari[12]以单自由度振动系统为对象,提出了同时描述结构服役长时效应和结构动力响应短时效应两个时间尺度的数字孪生方法．通过测量结构的无阻尼固有频率、阻尼系数或有阻尼固有频率的变化,反映结构质量和刚度的变化．在此基础上,Chakraborty和Adhikari[13]采用多专家模型学习以获取描述质量和刚度变化的系统参数的演化,但这种方法难以反映结构局部损伤的位置和大小的变化．

数字孪生涉及物理结构不同状态下大规模的数值模拟,高效的算法是关键．模型降阶是一有效途径．模型降阶方法主要有基于物理的模型简化法、投影法和代理模型法等．其中投影法得到了非常广泛的应用,包括本征正交分解法[14-15]、缩减基方法[16-19]、平衡截断[20-21]、模态截断[22]、Krylov子空间方法[23-25]等．其中,Krylov子空间方法具有算法稳定、容易实现、计算量小且适用于大型系统的优点．

本文针对受动载荷作用的结构,考虑结构服役过程中的损伤及其演化,研究了结构数字孪生体的构建方法．设计制作了考虑不同损伤位置和损伤程度的空间框架结构对方法进行验证,该方法为动态结构数字孪生体的构建奠定了基础．

1 数字孪生构建及模型降阶方法

1.1 数字孪生构建方法

物理实体结构在服役过程中可能出现各种状态．可以通过预先分析确定这些状态,包括承受的外载荷、结构原始无损伤状态、不同位置的损伤及其演化状态等．针对这些状态可以建立一个基于物理的模型库L={L1,L2,…,LN},其中N表示模型数量,库中每一个模型为对应于物理实体结构一种可能状态的数值模型．即使有些物理状态事先可能无法预料,也可以通过后续不断向模型库中添加,进行丰富和更新．在物理结构上特定位置布置传感器测量物理量Xt,如各个测量点的应变．利用模型库中的每一个模型计算其在不同载荷作用下的响应,获得训练数据,并结合机器学习算法训练获得一个数据驱动的模型选择器T．在物理实体结构服役阶段,该模型选择器根据物理实体上传感器的实测数据Xt推测模型库中的哪一个模型能最好地解释测量数据,从而将该模型用作当前时刻t的最新的数值模型dt．该过程可表达为

dt=T(Xt)∈L．

(1)

基于当前时刻的数值模型,快速给出计算结果,如结构位移、应力、应变．整个时程中均重复相同的过程,即根据各个时刻传感器测量数据不断推断当前物理实体结构的状态,从模型库中选择最匹配的数值模型计算给出结果．通过前述的整个过程,可以构建基于物理实体的数字孪生体,其能够捕捉物理结构上的变化并跟随其一同演化,快速甚至实时给出计算结果．

模型库中的模型包含描述物理实体结构在服役期间可能出现的状态,这些模型可以用微分方程描述,如有限元模型．一方面,精确地模拟一个完整系统需要很大的计算模型和极大的计算量;另一方面,数字孪生体需要跟随物理实体结构实时响应和演化,帮助做出诊断和决策;最后,要利用这些模型建立一个包含丰富数据的数据集以训练机器学习模型,获得模型选择器,这些都需要进行大量的模拟计算．因此有必要采用模型降阶方法,对所有模型进行降阶．

1.2 Krylov子空间模型降阶

为了对模型库中的数值模型进行降阶,本文采用Krylov子空间模型降阶方法．结构的动力学有限元方程可表示为

(2)

其中M,C,K∈n×n分别为结构有限元模型的质量、阻尼和刚度矩阵,F为等效结点载荷列向量,和分别为结点的位移、速度和加速度．对载荷列向量做变换,将式(2)改写成如下形式：

(3)

其中B∈n×m是常数矩阵,其描述结构所受载荷的分布,f∈m是结构的输入．

Krylov子空间降阶方法的基本思想是通过投影找到一个低阶模型,使其一定数量的“矩”和原模型匹配以近似原高阶模型．因此,需要找到一个可以直接应用于二阶微分方程(3)的投影．考虑如下投影：

a=Var,V∈n×r,a∈n,ar∈r,

(4)

其中r≪n．将式(3)乘以矩阵W∈n×r的转置,并将式(4)代入,得到一个阶数为r的降阶模型：

(5)

将上式写成

(6)

其中

Mr=WTMV,Cr=WTCV,Kr=WTKV,Br=WTB．

(7)

根据文献[25]的推导可知,如果式(5)中的矩阵V是输入二阶Krylov子空间Kr(-K-1C,-K-1M, -K-1B)的基,且其秩为r,矩阵W的选择使得矩阵WTKV非奇异,那么降阶模型和原模型的前r阶矩匹配．因此,通过构造输入二阶Krylov子空间,可以计算出W和V．为了简便,通常取W=V．最终得到一个阶数为r的降阶模型,其前r阶矩和全阶模型匹配．

文献[25]对Arnoldi算法[26]进行了扩展,给出了计算转换矩阵V的数值算法,其步骤如下：

2) 循环：i=2,3,…,r

(a) 计算向量

(b) 正交化,循环：j=1,2,…,i-1

(c) 标准化

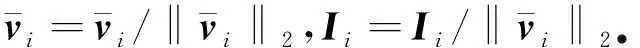
(d) 返回步骤(a)进行下一次循环直到r．

针对1.1小节模型库中的所有数值模型,均利用Krylov子空间方法建立其对应的降阶模型,用这些降阶模型替换库中的原始模型,最终构成一个降阶模型库L．

2 数据驱动数字孪生

2.1 训练数据集生成

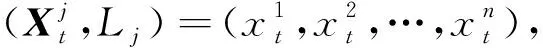
值得一提的是,对于静力学问题,结构所受载荷和其位移呈线性关系,且一一对应．但对于动力学问题,当前结构位移与载荷历程有关．对于动力学问题,根据d’Alembert原理,动力学方程可写成如下形式：

(8)

对于线弹性系统,方程右端等效载荷和位移呈线性关系,且一一对应,可等效为静力学问题．因此,在实际计算生成训练数据时,只要载荷范围足够大即可涵盖包含惯性力产生的等效载荷．实际计算时采用降阶模型进行计算．

2.2 基于机器学习的模型选择器

数字孪生体跟随物理结构一同演化时,需要根据物理结构上的传感器测量数据实时推断物理结构当前的状态,不断更新计算模型．因此,为了准确推断物理结构当前状态,从模型库中获取最匹配的模型,本文采用随机森林机器学习算法去训练一个模型选择器T．

随机森林机器学习算法[27]是一种基于决策树的集成学习算法．该算法是以决策树为基分类器的一个集成学习模型{h(X,Θk),k=1,2,…},其参数集{Θk}是独立同分布的随机向量．如图1所示,首先利用Bootstrap抽样从原始训练集中抽取k个样本,且每个样本的容量都与原始训练集一样;其次对k个样本分别建立k个决策树模型得到k种分类结果,最终的分类结果由单个决策树的输出结果投票决定．

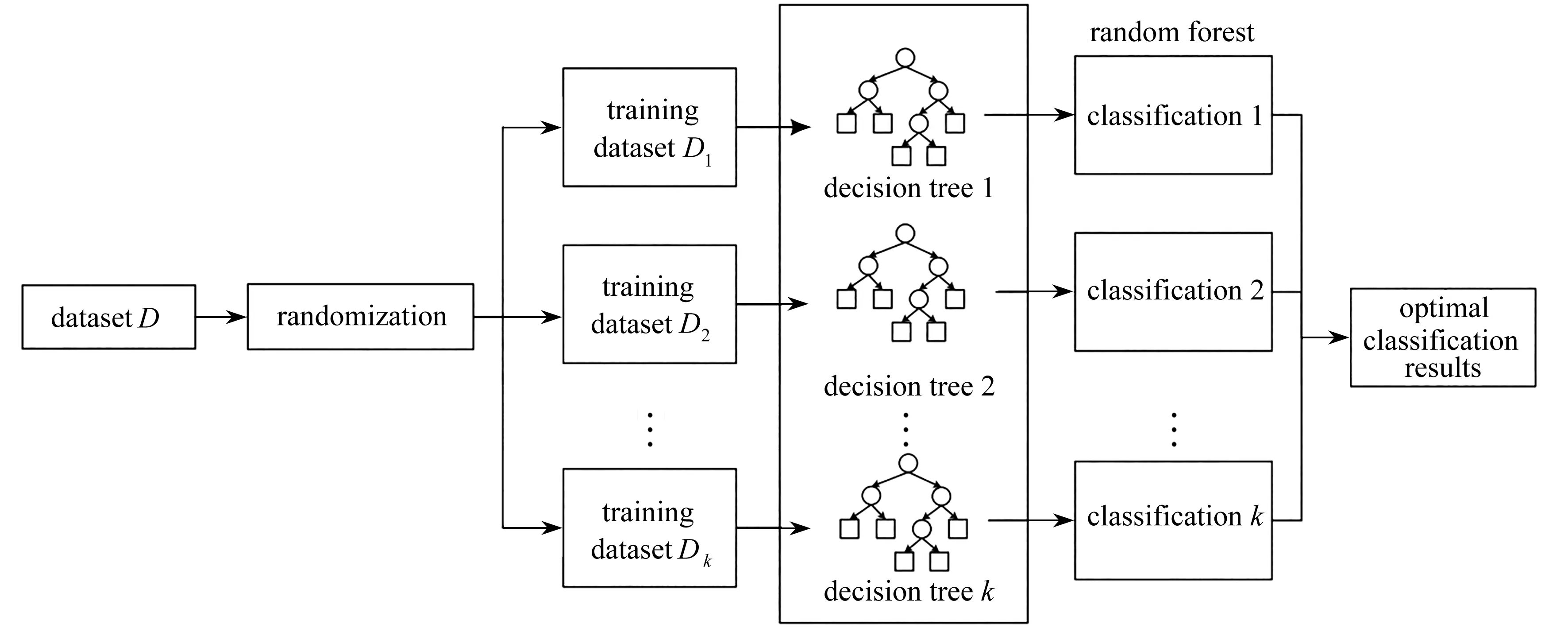
图1 随机森林算法示意图Fig. 1 The flowchart of the random forest algorithm

2.1小节得到的训练数据集D将作为随机森林机器学习的输入,通过分类训练获得模型选择器T,即建立起从传感器测点处的模拟数据到计算模型的映射关系．

2.3 数据驱动数字孪生及其演化

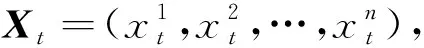
T：Xt→Lj．

(9)

通过前述方法可创建基于物理结构的数字孪生体,如图2所示．下标ti表示当前时刻,Sti表示该时刻的物理结构状态,Xti表示传感器测量数据,Lti为当前物理结构的计算模型,而Oti表示该时刻的计算结果,可以包括位移、应变和应力等．数字孪生体跟随物理结构一同演化,自动更新,实时完成计算．通过传感器的合理设置,还可以实时感知损伤的出现和演化,帮助决策者对结构的安全性做出实时预测和评估,确定是否需要采取相应措施．

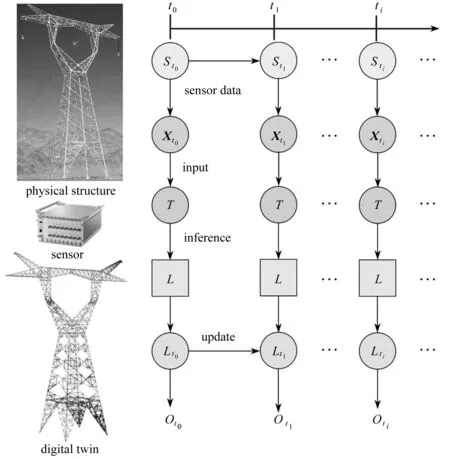
图2 物理结构与数字孪生体Fig. 2 The physical structure and the digital twin

事实上,根据实际情况和需要,数字孪生体还可以向物理实体结构发送反馈信息,通过驱动器实现主动控制,得到更广泛的应用．

假设传感器的采样频率为f,可以根据结构的响应频率范围设定驱动数字孪生模型的时间间隔Δt,对于前述柔性结构,Δt一般远大于传感器数据采样周期1/f．利用传感器数据驱动模型选择器后,立即利用选择的降阶模型计算结构响应,只要数据驱动孪生响应时间小于Δt,即可实现数据孪生体跟随物理实体结构实时演化．

如果由传感器数据驱动的当前时刻t+Δt的降阶模型为Li,该时刻的响应可以利用前一时刻t的响应,用Newmark方法时间积分得到．根据Newmark法,动力学有限元方程(2)的求解格式为[28]

(10)

对于当前的降阶模型Li,可利用如下降阶方程求解：

(11)

则降阶模型的速度和加速度为

(12)

最后利用映射关系(4)可计算全场量

(13)

进一步可以计算结构的应变和应力等．由于利用了降阶模型,式(11)—(13)的计算效率非常高,可实现实时反应．

值得一提的是,上述方法取决于结构的响应频率和数字孪生体的反应时间．对于受洋流或风荷载作用下的海底缆索、输电导线、杆塔、风力发电机等响应频率较低的结构,如风力发电机在风荷载作用下的响应周期达到10 s量级[29],结合模型降阶该方法可以实现数字孪生体的实时更新．另一方面,对于模型降阶后自由度很小的结构,该方法也适用于响应频率较高的情况．

3 例子：框架结构数字孪生体构建

以一个空间框架结构为例,制作物理实体模型,设计制作不同损伤程度的杆件,采用前述方法构建其数字孪生体,通过实验验证数字孪生体构建方法的正确性．

3.1 框架结构物理实体及测试系统

框架结构如图3所示．组成结构的每一根圆截面杆,半径为8 mm,构成结构边框的每根杆长度为400 mm,斜撑为542 mm．材料为铝合金6061,其密度、弹性模量、Poisson比分别为2.75 g/cm3,74 GPa,0.33．框架与4根刚性很大的立柱连接,立柱固定在基础上．为了模拟结构的损伤,除了完好杆件外,设计制作了部分带损伤的杆件．在杆件上特定位置改变圆杆的直径来反映损伤,直径越小表示损伤越大．无损伤杆件的直径为16 mm,表示损伤程度1和损伤程度2的杆件在损伤位置的直径分别减小到14 mm和12 mm．

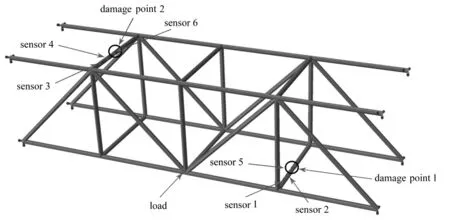
图3 空间框架结构示意图Fig. 3 Schematic diagram of the frame structure

假设框架结构在外载荷作用下,在特定的位置容易出现损伤．如图3所示,在损伤位置1和2附近分别设置两个应变传感器1、2和3、4,其测量数据作为模型选择器的驱动数据．为了验证该框架结构数字孪生体的准确性,在两个损伤杆件的损伤位置处各布置一个应变传感器5和6,如图3所示．

图4为该框架结构及其测试系统．为了方便杆件的替换,杆件之间采用连接板连接,连接板材料为Q235钢．可以将不同损伤程度的杆替换在框架中．载荷通过加载机构施加,加载机构与框架之间安装一个力传感器,其型号为JLBU-1-50KG,量程和输出灵敏度分别为50 kg和1.0 mV/V．在传感器位置沿杆轴向黏贴电阻应变片,其通过DH8302多通道动态应变仪连接笔记本电脑测量应变,数据采样频率为50 Hz．

图4 框架结构物理实体及测试系统Fig. 4 The physical frame structure and the test system

3.2 数字孪生体构建

按前述方法构建框架结构的数字孪生体．假设施加在结构上的载荷位置不变,结构总共有5种状态,构成有5个模型的模型库．如图5所示,对应于杆件无损伤的模型L1;损伤位置1发生损伤程度1(损伤处杆直径为14 mm)的模型L2;损伤位置1发生损伤程度2(损伤处杆直径为12 mm)的模型L3;损伤位置2发生损伤程度1和2对应的模型分别为L4和L5．

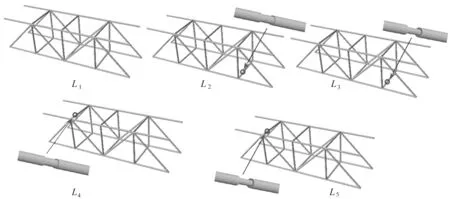
图5 框架结构模型库Fig. 5 The model library of the framework structure

针对这5个模型,分别建立有限元模型．用空间梁单元B31离散该框架结构,每一个模型均划分2 760个单元,自由度个数为16 560．分别计算得到各有限元模型的质量、阻尼和刚度矩阵M,C,K．其次,利用Krylov子空间模型降阶方法对各有限元模型降阶,得到对应的降阶模型Li,降阶模型的自由度r为100．数值计算表明,该框架结构采用原模型进行一次时间积分的时间为0.071 s,采用降阶模型为0.003 6 s,效率显著提高．值得一提的是,可以采用三维实体单元对结构模型进行离散,获得更高精度的有限元模型,并对其进行降阶．

利用该降阶模型库L,按照2.1小节的方法将计算模型上特征点处的应变模拟值作为训练数据,得到包含37 510个样本的数据集D,其中划分的数据集的数量k取20．选择其中70%的样本用作随机森林机器学习的训练样本,训练得到模型选择器T．余下30%作为测试集,利用训练得到的模型选择器对测试数据进行分类预测,模型预测分类与实际分类的混淆矩阵如图6所示,可见模型选择器分类的错误率仅为1.32%,具有较高分类精度．

图6 模型选择器测试数据混淆矩阵Fig. 6 The confusion matrix of the testing sample

3.3 实验验证

对如图4所示框架结构加载点施加动态载荷,力传感器和应变传感器1～6的采样信号通过动态应变仪输入笔记本电脑记录载荷和应变时程．将加载过程中的任一时刻,应变传感器1～4测量得到的应变输入数字孪生体,驱动模型选择器T迅速推断当前时刻框架结构的状态,并从模型库中选择最匹配当前框架结构状态的计算模型,进而利用力传感器测量得到的当前时刻的载荷快速计算结构的位移、应变和应力,下一时刻重复相同的过程,数字孪生体便可以实时输出整个加载过程中任意时刻框架结构的变形和应力．将各个时刻位于损伤区域处的传感器5和6的应变实测值与数字孪生体的输出结果进行比较,以验证孪生体的精度．

由于有限元模型没有考虑结构中的连接板和螺栓, 实验过程中发现螺栓预紧力影响较明显．如果要考虑螺栓的影响, 在建立有限元模型时需考虑连接板处的细节等．经反复调节螺栓预紧力实验得到了较好的结果, 图7为结构完好和两个位置分别出现损伤时实测值与数字孪生体预测结果的比较．图中给出了力传感器测得的载荷时程、传感器1～4测得的应变时程以及传感器5和6的应变实测值与数字孪生的预测值．注意传感器1～4测得的应变是模型选择器的驱动数据．从图中可见, 数字孪生体预测的损伤位置的应变时程与实测值比较接近, 表明建立的数字孪生体能够反映物理结构的损伤状态．值得一提的是, 数字孪生体给出的损伤位置的应变曲线, 在特定位置出现了波动, 而对应时刻的载荷却没有波动．这可能是模型选择器T未能100%的正确选择匹配模型, 从而在这些时刻根据传感器输入数据错误推断了物理实体状态, 导致在载荷未发生波动的情况下应变发生了波动．然而, 从图中曲线可见, 这种波动并未对数字孪生后续的预测结果产生大的影响．图8给出了当框架结构损伤位置2出现损伤程度2时, 其数字孪生体给出的典型时刻的应变分布．

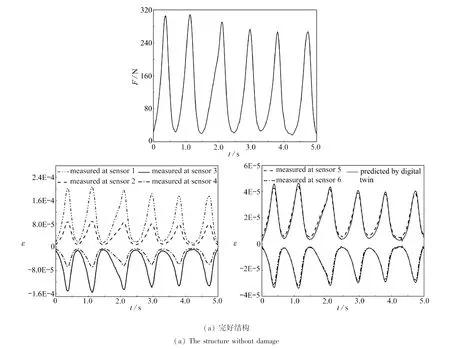
图7 结构实测与数字孪生预测结果比较Fig. 7 Comparison of measured values and predicted results by digital twin

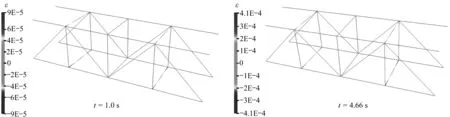
图8 框架结构数字孪生体给出的典型时刻的应变分布Fig. 8 Strain distributions at typical moments predicted by the digital twin of the frame structure

为了反映该框架结构数字孪生体在结构损伤演化过程中的更新,假设损伤位置2在受载过程中从初始完好状态变成损伤状态,首先采用有限元模拟得到传感器1～4的应变,然后将其作为传感器的实测数据,模拟数字孪生体随物理结构的演化过程．图9给出了结构损伤位置2处损伤程度发生两次变化时,数值孪生体的更新和输出结果．结构在开始是无损伤完好状态,在1.8 s时损伤位置2发生了损伤,之后在4.48 s时该处损伤进一步加大．从图中可见,损伤位置2处应变传感器6和其相邻位置的传感器4的应变时程曲线在这两个时刻均发生了明显变化．结果表明,一方面数字孪生体在这两个时刻实现了实时更新,另一方面可以通过在易出现损伤的位置附近布置传感器监测损伤的发生．

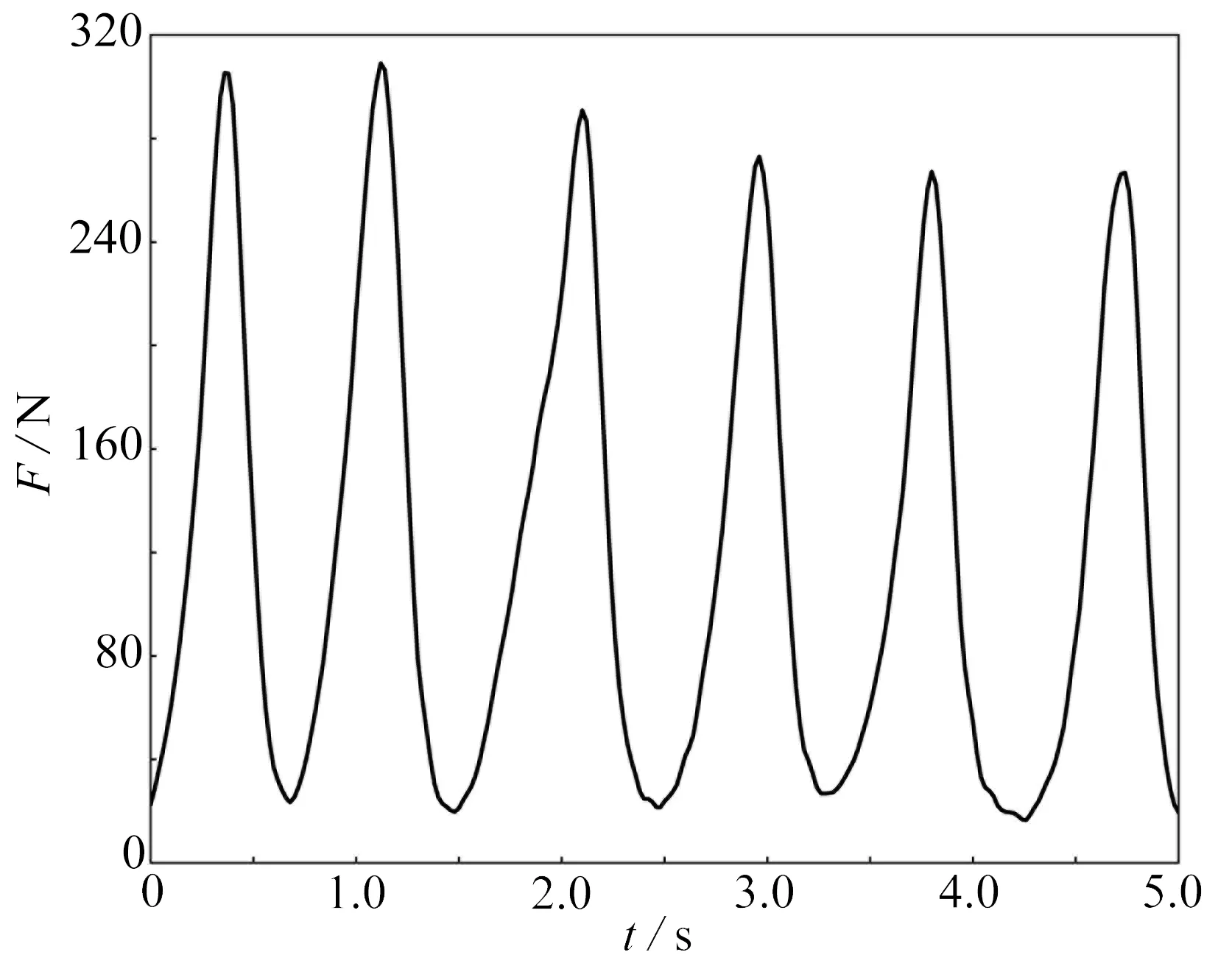
图9 位置2损伤演变过程中数字孪生体的更新Fig. 9 Update of the digital twin during evolution of damage at point 2

4 结 论

本文针对受动载荷作用结构,提出了一种基于降阶模型和机器学习的动态结构数字孪生构建方法,并利用框架结构对方法进行了验证．得到如下结论：

1)采用Krylov子空间模型降阶方法对结构动力学有限元方程进行降阶,大大降低了模型自由度,提高了模型计算效率,可以用于数字孪生体的建模;

2)本文提出的动态结构数字孪生方法,对于响应频率较低的柔性结构,以及响应频率较高且模型降阶后自由度较小的情况,均可实现数字孪生体随物理结构的实时更新;

3)通过传感器的合理布置,建立的数字孪生体可以预测结构的损伤及其演化．

本文针对动态结构提出了数字孪生构建方法的框架,尚需进一步对不确定性因素和传感器采样信号噪声的影响等进行深入系统的研究．