特征函数的性质在实变函数中的应用
石秀文
(邢台学院,河北邢台 054001)
在实变函数中讨论集合的基数与对等、可测函数及函数的积分等问题时,常常用到特征函数,如果熟悉特征函数常用性质,并能熟练掌握应用特征函数的性质解决问题的一般思想,有助于提高学生分析问题和解决问题的能力。下面将探讨利用特征函数的性质解决实变函数中某些问题中一般思想方法。
1 特征函数及常用的一些性质
1.1 特征函数的定义
显然,若A是可测集S的可测子集,φA(x)则是S上非负可测函数,也是可积函数且
1.2 常用的几个特征函数的性质
性质 1:设 A,B⊂S,则 A⊂B⇔φA(x) ≤φB(x),x∈S(单调性),φA(x)=φB(x),x∈S⇔A=B(一对一性质)。
性质2:(特征函数与简单函数的关系) 若f(x)=ci,x∈Ei,i=1,2…n,是 E 上的简单函数,则 f(x)互不相交。
性质4:(积分等式)若f(x)在可测集E的可测子集E0及收敛,可测子集列En上可积,则有等式

2 特征函数性质的应用
2.1 “一对一性质”在集合对等问题中的应用
集合的基数是集合的重要属性,研究集合的基数是通过集合对等的关系来确定,建立集合间的——对应关系是确定对等的基本方法,如果难于建立集合间的一一对应关系,常用Bernstein定理来判断对等并确定其基数。特征函数与集合间的一对一性质,对讨论某些集合间对等有着重要的作用。
例1:设S是可数集,S的所有子集构成的集合为2S,求2S的基数。
解:由集合对等与基数的定义可知:对等集合的所有子集构成的集合族仍对等。不妨设为非负有理数集合为 S= {r1,r2,…rn,…… },∀A∈2S,令
设 φA(rn)=an,n=1,2,3,……;令 x=0.a1,a2,a3……,则 0≤x=0.a1,a2,a3……<1,即 x∈[0,1]。
由一对一性质,2S与 [0,1]的一个子集对等,所以(c为[0,1]的基数)。
反之,对∀x∈[0,1],可表示为唯一的无限小数0.b1,b2,b3……,可设对应的非负有理数构成的集
显然,此映射是一对一的,故 [0,1]与2S的一个子集对等,所以综上。
由此可见,通常讨论某集的所有子集构成的集合2S的基数问题或集合族与其他集合对等问题时,可考虑应用定义在S上关于其子集的特征函数,通过特征函数“一对一”性质,建立2S与相关集合或其子集的一一对应关系来解决问题。
2.2 可测函数与特征函数的关系的应用
可测函数与简单函数的关系:f(x)是可测集E⊂Rn上可测函数的充要条件是存在一列简单函数ψm(x),使得
而由性质2可知简单函数ψm(x)是一组特征函数的线性和。因此,讨论可测函数问题,就可以归结为最简单的特征函数问题,“由特征函数到简单函数,再向一般可测函数过度,这在许多场合都是行之有效的办法。”
例 2:设 f1(x)、f2(y)分别是 E1⊂Rp、E2⊂RqS上可测函数,证明:f1(x)×f2(y)是 E1×E2⊂Rp×Rq上可测函数。
解析:证明有具体表达式函数的可测性,用定义直接证明较为简便;证明抽象函数可测性,可考虑用“可测函数与特征函数的关系”进行推理论证。
设f(x,y)=f1(x)×f2(y)
(1)若fi(x)是可测子集Ei上特征函数,则f(x,y)是E1×E2上特征函数,可测集上特征函数是可测函数,故结论成立。
(2)若fi(x)是Ei简单函数,则f(x,y)是E1×E2上简单函数(易证),故是可测函数。
(3)fi(x)是一般可测函数,由可测函数与简单函数的关系,存在简单函数列 gm(x),hm(y),使得:f1
令 ψm(x,y)=gm(x)×hm(y),也是 E1×E2上简单函列,且
故结论成立。
此例证明思路是由简单到复杂,即由特征函数成立——简单函数成立——一般可测函数成立,这种由特征函数逐渐递进到一般可测函数的证明,是实变函数中常用的方法。
2.3 特征函数积分性质的应用
设f在E及其可测子集E0上可积,常用的两个等式:若存在,由控制收敛定理及极限性质:
证明:对任意可测子集A⊂E,φA(x) 在E有界可积,故由A的任意性可知:
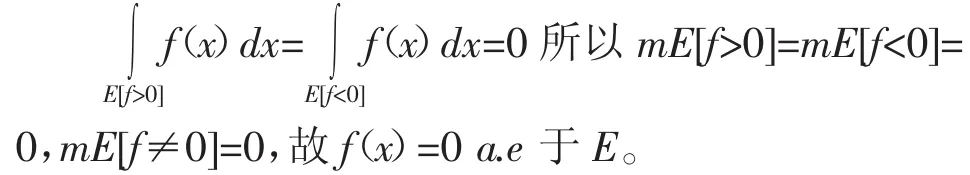
可见利用等式(1)通过特征函数巧妙的将E上的积分转化为其任何子集上的积分使其为零,体现了特征函数在积分问题中的作用。一般的,当涉及到某集合上的积分与之子集上的积分关系时,可考虑应用这一性质进行转化。
例4:设函数f在E上可积,可测集列En⊂存在,则
(2) 由可积性知,f在En上可测,而[a,b],故 f在 [a,b]上可测.构造函数列:fn(x)=φEn则fn(x)在E上可测,由En⊂En+1,由特征函数单调性,可知 fn(x)≤fn+1(x),所以 fn(x)→f(x)于E。
例6:若设f,g在可测集E上非负可测,则对∀a∈R1,mE(f≥a)=mE(g≥a),则
解析:E=E[x;f(x)≥0]=E[x,g(x)≥0],
(2) 否则f,g在E上几乎处处有限(不妨设处处有限),由已知条件可知:mE(a≤f≤b)=mE(a≤f)-mE(b≤f)=mE(a≤g≤b),∀a,b∈R1。于是∀n,令 En=E[0≤f≤n]=E[0≤g≤n],Fn=E[n≤f]=E[n≤g],E=En∪Fn
∀n,将En作互不相交分解:其中,令 Fn=En,n2*,由集En,k的特征函数来构造E上单调递增简单函数列:(x),则∀x∈E,∃n,使得f(x)∈[0,n]
此例中,利用特征函数构造如上的简单函数列,该函数列在E上收敛于可测函数f(x),这是实变函数中特征函数应用的一个典型的方法,对讨论某些可测函数与积分问题有着重要作用。

