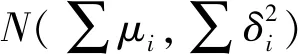随机变量的特征函数在概率论中的应用
白伟华
(韶关学院 韶州师范分院数学系,广东 韶关512009)
0 引言
在概率论中,随机变量的分布函数刻画了随机变量的统计规律。但有时分布函数或概率密度这些工具使用起来并不方便,如计算独立随机变量和分布的概率密度,用卷积求很麻烦,过于复杂,通过数字特征并不能完全反映出随机变量的分布规律,但确定它的特征函数比较容易。由于分布函数和特征函数之间有一一对应关系,在得知特征函数后就可知道分布函数。经过不断探索与研究,发现特征函数是处理许多概率论问题的有力工具。
1 有关概念及结论
现将本研究中涉及的有关概念及结论列举如下,不予证明,详见(1)(2)。
1.1 特征函数的定义
设x是随机变量,称复随机变量eitx=costx+isintx的数学期望。
fx(t)=E(eitx)=E(costx)+iE(sintx),-∞ (1) 为x的特征函数。 因为对任何实数t,E|costx|≤1,E|sintx|≤1, 所以fx(t)对一切实数有定义,即任一随机变量的特征函数总是存在的。 当离散型随机变量x的分布律为:pk=p(x=xk),k=1,2,… 则x的特征函数: (2) 当连续型随机变量x的概率密度函数为p(x), 则x的特征函数: (3) ①fx(o)=1, |fx(t)|≤1 -∞ ③设y=ax+b,其中a,b是常数,则fy(t)=eitbfx(at) ④设x,y独立,则fx+y(t)=fx(t)·fy(t) 若x是连续型随机变量,其概率密度函数为p(x),有特征函数fx(t),则有 设随机变量x的分布函数为F(x),有特征函数f(t),x1与x2为F(x)的任意两个连续点,则有 例2:试证f(t)=cost为一特征函数,并求它所对应的随机变量x的分布。 例3:设随机变量x服从参数为α,β的Γ分布,求其数学期望和方差。 且iE(x)=f′(0),i2E(x2)=f″(0); 由于分布函数和特征函数之间有一一对应的关系,从而知: 例5:设x1,x2和x3是相互独立的,且服从正态分布N(0,1),试求随机变量Y1=x1+x2和Y2=x1+x3组成的(Y1,Y2)的分布。 解:(Y1,Y2)=(x1+x2,x1+x3) ∵xi~N(0,1),i=1,2,3, ∴(x1,x2,x3)~N(0,E3), 从以上5个例子可以看出,有些概率问题利用分布函数很难给出证明,即使能给出证明也很麻烦,而利用特征函数及其导数性质便可很巧妙地给出证明,这充分说明了注重知识的内在联系是很重要的。


1.2 特征函数的性质


1.3 特征函数的唯一性定理
1.4 特征函数的逆转公式
2 特征函数的应用
2.1 求随机变量的分布



2.2 求随机变量的数字特征
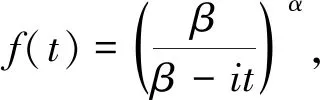


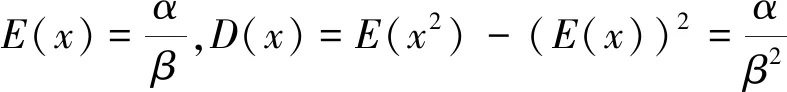
2.3 求独立随机变量和的分布