特征函数在伽玛分布中一个恒等式的证明及推广
2017-11-15 06:01:52
数码设计 2017年14期
(四川民族学院理工学院 四川 康定 626001)
引言:特征函数是处理概率论问题的一个有力工具,但在实际的概率分析中直接利用分布函数、概率密度函数与分布列的情况较多[1].但在许多方面,特征函数比分布函数等具有更好的分析性质[2].本文使用特征函数证明了伽玛分布中的一个恒等式,并对恒等式的几种特殊情况予以了探讨。
1 特征函数的定义及其性质
定义[1]设X为一随机变量,则称φ(t)=E(eitx),-∞ 当X为离散型随机变量时,有分布列pk=p(X=xk),k=1,2,…则X的特征函数为 当X为连续型随机变量时,有概率密度函数p(x)则X的特征函数为 引理[1]若E(Xl)存在,则X的特征函数为φ(t),可l次求导,且对1≤k≤l,有 φ(k)(0)=ikE(Xk) … 证明 当α=n时,Γ(n)=(n-1)!,即有 定理3的结论亦可多次使用分部积分法算出,但运算量较大,使用本文的方法可以快速得出结论,化简计算. 定理5 当α=n,λ=1,为正整数时,令m=n+k-1有 证明 当α=n时,Γ(n)=(n-1)!,即有 定理5给出了数字阶乘与定积分之间的一个等式,有助于进一步理解阶乘与积分之间的一些联系. 本文以特征函数论证了伽玛分布中的一个恒等式,并对这个恒等式的几种特殊情况予以了讨论.对于有些恒等式的证明.使用特征函数将使得证明更加巧妙与简单,把这种方法推广到其他分布的某些恒等式的证明之下,也具有良好的分析性质。


2 利用特征函数φ(t)证明Ga(α,λ)中的一个恒等式
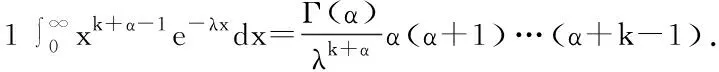



3 Ga(α,λ)中的一个恒等式的推广







4 结语
猜你喜欢
广西民族大学学报(自然科学版)(2022年1期)2022-05-18 05:18:06
数学年刊A辑(中文版)(2020年1期)2020-05-19 00:30:48
黑龙江科学(2020年5期)2020-04-13 09:14:04
邢台学院学报(2018年4期)2018-12-14 11:11:56
当代旅游(2018年8期)2018-02-19 08:04:22
电子制作(2017年14期)2017-12-18 07:07:52
中国医学装备(2015年10期)2015-12-29 12:00:24
四川师范大学学报(自然科学版)(2015年3期)2015-02-28 14:07:59
化工自动化及仪表(2014年2期)2014-08-02 01:43:26
现代电子技术(2014年4期)2014-03-05 18:18:26

