因子von Neumann代数上非线性*-Lie导子的刻画

庞永锋, 张丹莉, 马 栋

(西安建筑科技大学 理学院, 西安 710055)

0 引 言

a(λb+μc)=λ(ab)+μ(ac), (λb+μc)a=λ(ba)+μ(ca), ∀a,b,c∈A,λ,μ∈F,

则称该映射是A上的一个乘法， 称A是一个可结合代数. 如果Banach空间A上的乘法满足: ∀a,b∈A, ‖ab‖≤‖a‖‖b‖, 则称A为一个Banach代数.如果代数A上的映射A→A,aa*满足

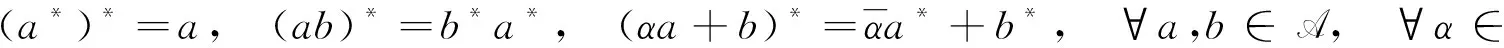
则称该映射是A上的对合运算， 称A是一个可结合*-代数.如果Banach代数A上的对合运算满足对于任何a∈A有‖a*a‖=‖a‖2, 则称A是C*代数.如果A是C*代数且单位元1满足1*=1, 则称A是含单位元的C*代数[4].

目前, 关于*-导子相关性质的研究已引起广泛关注.设A和B是两个因子von Neumann代数, Cui等[5]证明了非线性双射Φ： A→B对任意的A,B∈A, 有Φ([A,B]*)=[Φ(A),Φ(B)]*当且仅当Φ是*-环同构; Li等[3]证明了非线性映射Φ： A→B对任意的A,B∈A, 有Φ(A·B)=Φ(A)·Φ(B)当且仅当Φ是*-环同构; Taghavi等[1]证明了因子von Neumann代数上的*-Jordan导子是可加*-导子; Yu等[2]证明了因子von Neumann代数上的*-Lie导子是可加*-导子; 张芳娟[6]证明了含单位元的C*代数上的可加的广义*-Lie导子是一个保*的可加导子; 孔亮[7]证明了φ是因子von Neumann代数上的非线性*-Jordan导子当且仅当φ是非线性*-Jordan三重导子; Li等[8]证明了因子von Neumann代数上的非线性混合Lie三重映射是可加*-导子; Fu等[9]证明了无中心交换投影的von Neumann代数上的非线性斜Lie三重导子是*-导子.

设H是 F上的一个Hilbert空间,I表示H上的恒等算子, 0表示H上的零算子,B(H)表示H上所有有界线性算子构成的代数, M⊆B(H)是一个von Neumann代数.M的换位子为M′={T∈B(H),TA=AT, ∀A∈M}, M的中心为M∩M′, 记为Z(M).如果M的中心是平凡的, 即Z(M)=I, 则称M是因子von Neumann代数.因子von Neumann代数M是素的, 即∀A,B∈M,AMB={0}A=0或B=0.

1 预备知识

设M是Hilbert空间H上维数大于1的因子von Neumann代数,P1∈M是一个非平凡投影,P2=I-P1.记Mij=PiMPj,i,j=1,2.

定义1若φ: M→M满足

则称φ是M上的非线性*-Lie三重导子.

引理1[8]设A∈M, 若∀B∈M有AB=BA*, 则A∈I.

引理2[5]设A∈M, 若∀B∈M有AB=B*A, 则B=0.

引理3若φ: M→M是非线性*-Lie三重导子, 则:

1)φ(I)⊆I;

2) 若A*=A, 则φ(A)*=φ(A);

3)φ(I)⊆I;

4)Piφ(Pi)Pj=-Piφ(Pj)Pj, 1≤i≠j≤2;φ(Pi)=P1φ(Pi)P2+P2φ(Pi)P1,i=1,2.

证明： 根据φ的定义可得

φ(0)=φ(000-000*)=φ(0)00+0φ(0)0+00φ(0)-φ(0)00*-0φ(0)0*-00φ(0)*=0.

1) ∀λ∈及∀T∈M, 有

将式(1)和(2)相加, 可得φ(λI)T-Tφ(λI)*=0.由T的任意性及引理1可知,φ(λI)∈I.由λ的任意性可得φ(I)⊆I.

2) 由φ(I)∈I, 则Aφ(I)=φ(I)A.由A*=A, 则

因此φ(A)*=φ(A).

3) 由φ(I)∈I, 则Bφ(I)=φ(I)B.∀λ∈,B∈M且B*=B, 有φ(B)*=φ(B), 且

故Aφ(λI)=φ(λI)A.由A的任意性可得,φ(λI)∈M∩M′=I.由λ的任意性, 则φ(I)⊆I.

将式(3)左乘P1可得P1φ(P1)P2+P1φ(P2)P2=0, 即P1φ(P1)P2=-P1φ(P2)P2.将式(3)右乘P1可得P2φ(P2)P1+P2φ(P1)P1=0, 即P2φ(P2)P1=-P2φ(P1)P1.

对任意的A12∈M12, 有

将式(4)左乘P1、右乘P2可得P1φ(P1)A12P2=0.由A12的任意性及M的素性可得P1φ(P1)P1=0.由φ(0)=0, 有

化简式(5)可得

P2φ(P1)A21=A21φ(P1)P2+A21P1φ(P2).

(6)

将式(6)右乘P2可得

0=A21φ(P1)P2+A21P1φ(P2)P2=P2A21(φ(P1)P2+P1φ(P2)P2).

由A21的任意性及M的素性可得

φ(P1)P2+P1φ(P2)P2=0.

(7)

将式(7)左乘P2可得P2φ(P1)P2=0, 故φ(P1)=P1φ(P1)P2+P2φ(P1)P1.

同理可得

化简式(8)可得

P1φ(P2)A12=A12φ(P2)P1+A12P2φ(P1).

(9)

将式(9)右乘P1可得

0=A12φ(P2)P1+A12P2φ(P1)P1.

由A21的任意性及M的素性可得

φ(P2)P1+P2φ(P1)P1=0.

(10)

将式(10)左乘P1可得P1φ(P2)P1=0.

对任意的A21∈M21, 有

将式(7)左乘P2、右乘P1可得P2φ(P2)A21P1=0.由A21的任意性及M的素性可得P2φ(P2)P2=0.故φ(P2)=P1φ(P2)P2+P2φ(P2)P1.

设T=P1φ(P1)P2-P2φ(P1)P1,A∈M, 定义映射Φ: M→M为Φ(A)=φ(A)-[A,T], 其中[A,T]=AT-TA.

引理4映射Φ是M上的一个非线性*-Lie三重导子.

证明： ∀A,B,C∈M, 有

因此Φ是M上的非线性*-Lie三重导子.

引理5设Φ是M上的一个非线性*-Lie三重导子, 则Φ(P1)=0,Φ(P2)=0.

证明： 由引理3中4)可得,

引理6设Φ是M上的一个非线性*-Lie三重导子, 则Φ(Mij)⊆Mij,i,j=1,2.

证明： 设Aij∈Mij, 1≤i≠j≤2, 则

将式(12)左右同乘Pi可得PiΦ(Aij)Pi=0.由Pi=I-Pj及式(12)可得,

将式(13)左右同乘Pj可得PjΦ(Aij)Pj=0.类似地, 有

将式(14)左乘Pj可得PjΦ(Aij)Pi=0.因此Φ(Aij)=PiΦ(Aij)Pj∈Mij.

设Aii∈Mii,i=1,2且k≠i, 则有

将式(15)左乘Pi可得PiΦ(Aii)Pk=0; 将式(15)右乘Pi可得PkΦ(Aii)Pi=0.

对任意的Bik∈Mik(1≤k≠i≤2), 由Φ(Bik)∈Mik, 则

将式(16)左乘Pi可得PiBik(PkΦ(Aii)Pk)=0.由M的素性可得PkΦ(Aii)Pk=0.因此Φ(Aii)=PiΦ(Aii)Pi∈Mii.综上可得Φ(Aij)∈Mij, 故Φ(Mij)⊆Mij.

引理7设Φ是M上的一个非线性*-Lie三重导子, ∀A11∈M11及∀A12∈M12, 则P1Φ(A11+A12)P2=Φ(A12).

证明： ∀A12∈M12, 由引理4和引理6可得,

将式(17)左乘P1、右乘P2可得

P1Φ(A11+A12)P2=P1Φ(A12)P2=Φ(A12).

引理8设Φ是M上的一个非线性*-Lie三重导子, 则Φ(I)⊆I且Φ(I)=0.

证明： ∀λ∈, 由引理3中1)及Φ的定义可得,

Φ(λI)=φ(λI)-[λI,T]=φ(λI)∈I.

由λ的任意性可得Φ(I)⊆I.因此∃α∈, 使得Φ(I)=αI.

∀A12∈M12, 由引理5可得,

将式(18)左乘P1、右乘P2, 由引理6和引理7可得,

Φ(A12)=P1Φ(A12)P2=αP1A12P2+P1Φ(A11+A12)P2=αA12+Φ(A12).

(19)

对式(19)化简可得αA12=0, 由A12的任意性可得α=0, 即Φ(I)=0.

2 主要结果

定理1设M是复Hilbert空间H上的因子von Neumann代数, 且dim M >1.如果Φ: M→M是一个非线性*-Lie三重导子, 则Φ是非线性*-Lie导子.

证明： 由引理8及Φ的定义可得,

因此Φ是一个非线性*-Lie导子.

注意到上述条件实际上是一个充要条件.由文献[5]中定理2.1, 当Φ是非线性*-Lie导子时, 则Φ是可加*-导子.因此Φ是非线性*-Lie三重导子.