单自由度系统
田红亮 陈 谦
(三峡大学 机械与动力学院,湖北 宜昌 443002)
1 单自由度系统对任意激励力的响应
在任意激励力的作用下,有阻尼单自由度系统的运动微分方程[1]为
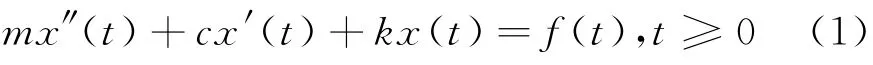
开始时刻(t=0)的初位移和初速度分别为

式(1)可变形

1812年拉普拉斯在《概率的分析理论》中总结了当时整个概率论的研究,论述了概率在选举、审判调查、气象等方面的应用,并导入“拉普拉斯变换”.f(t)的拉普拉斯变换[2]为
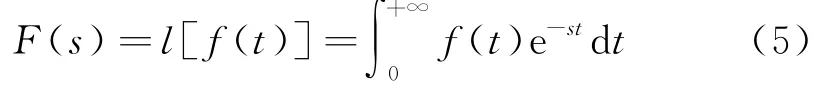
函数f(t)求导后取拉普拉斯变换

将式(5)代入式(6),得

由式(7)得
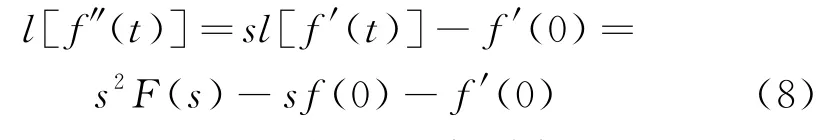
由式(7)和(8),可得式(4)的拉普拉斯变换


X(s)的2个单极点满足
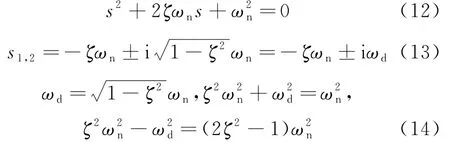
海维赛德第一类展开式为

式中,s1,s2,…,sn为B(s)的n个单零点.
由式(15),可得以下象函数的拉普拉斯逆变换
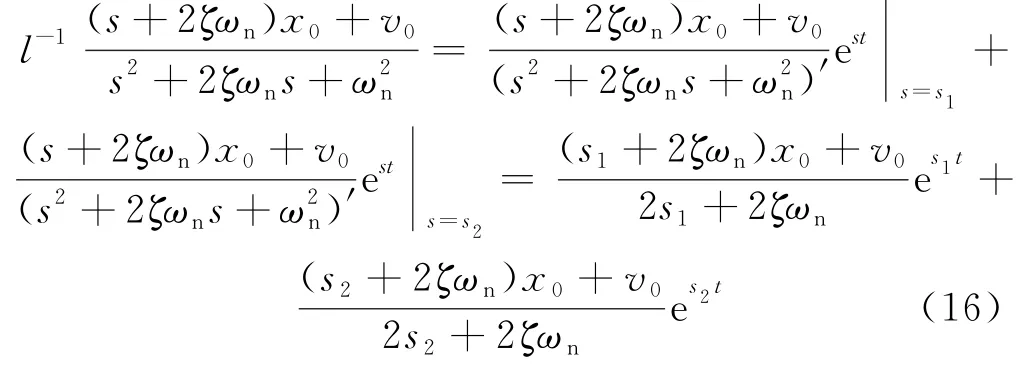
将式(13)代入式(16),得

由式(15),可得以下象函数的拉普拉斯逆变换

将式(13)代入式(19),得

由式(11)得

将式(18)代入式(21),得

两个函数卷积的拉普拉斯变换[3]为

上式右端的积分叫做先对τ、后对t的二次积分.这个积分也可以写成先对t、后对τ的二次积分

令t-τ=u,则

将式(25)代入式(24),可得卷积定理

按照式(27),可将式(22)展开

将式(20)代入式(28),得

故在任意激励力下单自由度系统的通解为
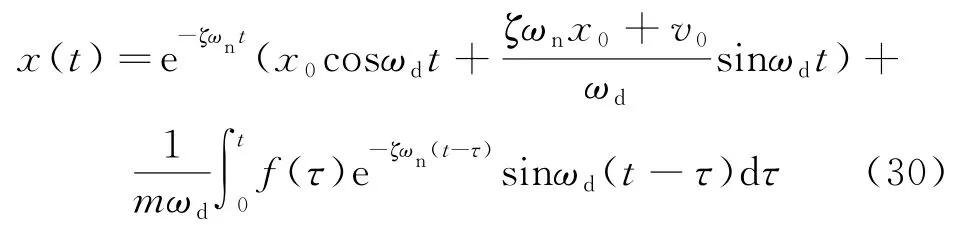
令t-τ=u,容易验证卷积运算满足交换律
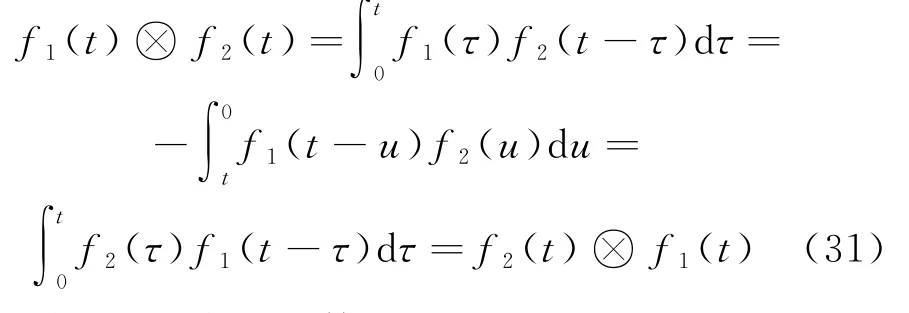
由式(31),式(29)等于

故任意激励力下在某一时间t,单自由度系统的位移为

设f(x)在闭区间[a,b]上连续,令x=a+bu,则存在恒等式

根据式(34),可知式(30)与(33)相等.
2 单自由度系统一般解的证明
式(30)的第一项为

将式(14)的第二式代入式(36),得


将式(14)的第三式代入式(38),得
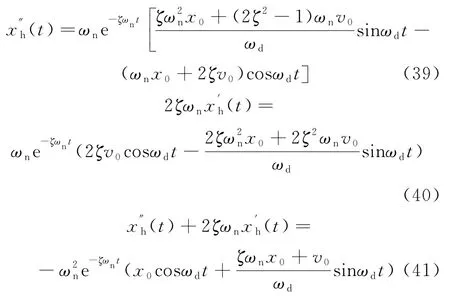
将式(35)代入式(41),得

故xh(t)是式(4)对应的齐次方程的通解.
式(30)的第二项为

如果函数f(x,y)及其对自变量x的偏导函数f x(x,y)都在矩形R=[a,b]×[c,d]上连续,函数α(x)和β(x)都在闭区间[a,b]上可微,且c≤α(x)≤d,c≤β(x)≤d,a≤x≤b,则莱布尼茨公式[4]为
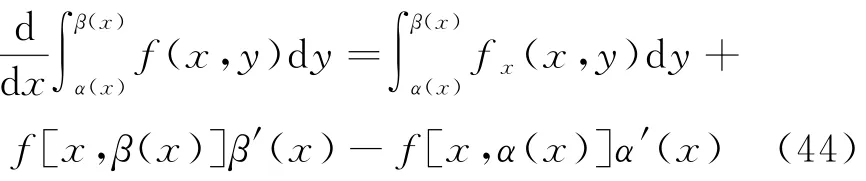
应用莱布尼茨公式(44),得

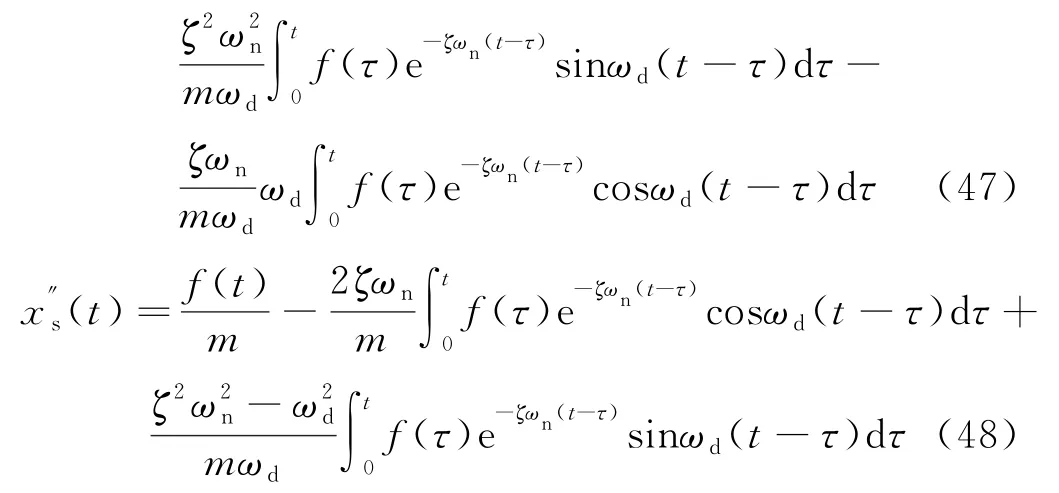
将式(14)的第三式代入式(48),得

将式(43)代入式(51),得
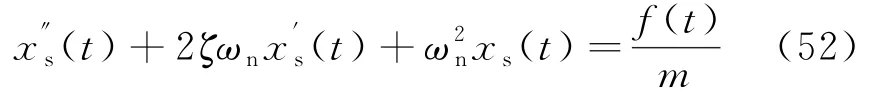
故xs(t)是非齐次方程(4)的一个特解.
由式(30)得

式(53)与式(2)相同.

将式(37)和(46)代入式(55),得
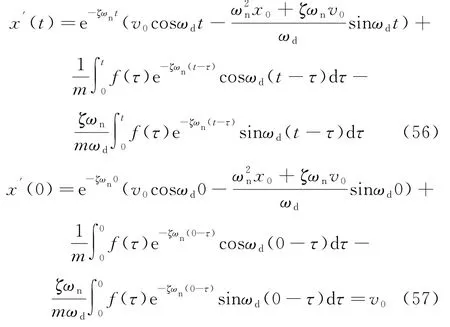
式(57)与式(3)一致.
3 工程实例和结果分析
3.1 阶跃激励力的响应
阶跃激励力为

式中,u(t)为单位阶跃函数.
0初始条件时,将式(58)代入式(33),得

将式(14)的第二式和第一式代入式(60),得

由直角坐标x,y得到极坐标[5]
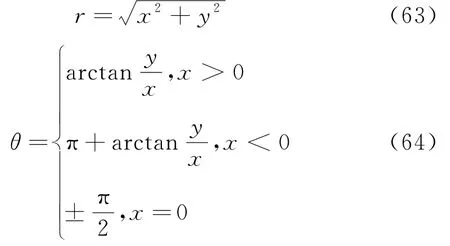
则三角函数的加法公式为

按照式(65),式(61)可化简
按照式(66),式(61)可化简

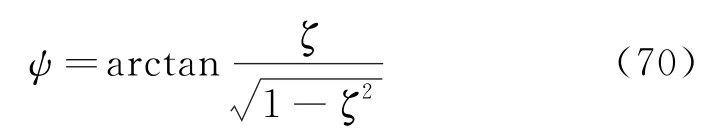
当m=85 kg,k=5000 N/m,c=15 N·s/m,F=5 000 N时,系统的响应曲线如图1所示.
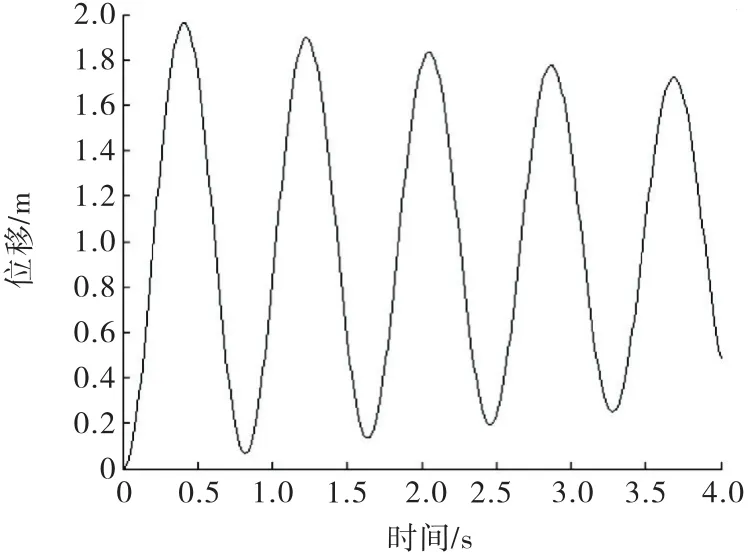
图1 阶跃激励力的响应
3.2 矩形单脉冲激励力的响应
矩形单脉冲激励力为

将式(71)代入式(33),得

1)当0≤t≤td时的响应
式(72)等于式(59),进一步等于式(61)
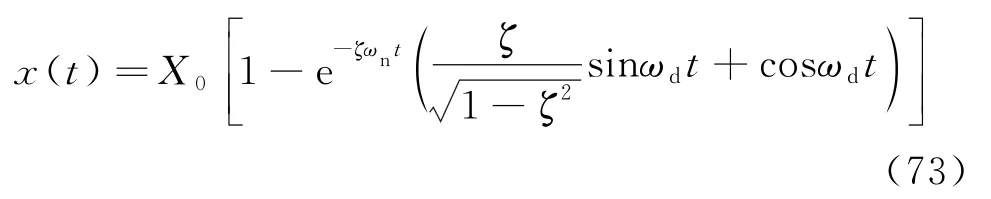
当ζ=0时,式(73)退化为
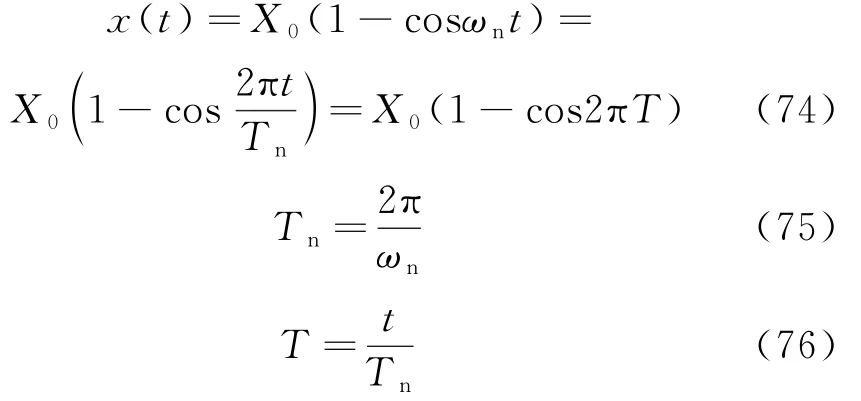
2)当t>td时的响应
式(72)等于


当ζ=0时,式(78)蜕化为
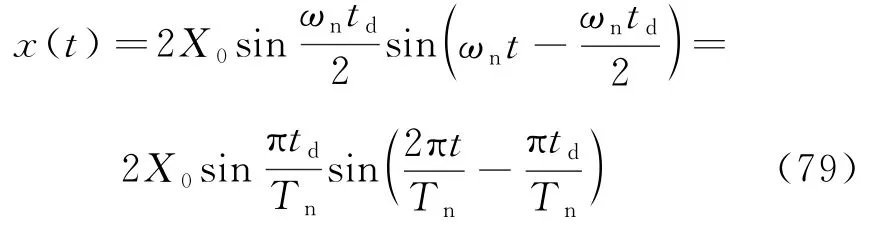
式(79)可简化
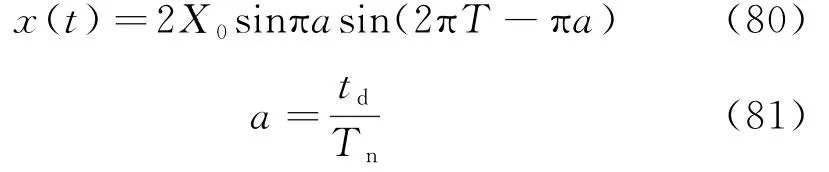
综合式(74)和式(80),得

系统的响应曲线如图2所示.

图2 矩形单脉冲激励力的响应
4 结 论
有阻尼单自由度系统强迫振动解析解的构建,有助于分析有阻尼多自由度系统,此外,还可以探讨提高冲击减振器快速耗能性能的途径,比较不同修改方案的能量耗散情况和抑振效果.

