基于粒子群算法和增广拉格朗日乘子法的混合可靠性分析
王林军 廖 玮 王 锬 杜义贤
(三峡大学 机械与动力学院,湖北 宜昌 443002)
可靠性是结构设计达到设计标准,能够保证结构有效稳定的工作,而不发生破坏的重要指标[1].目前,由于受到制造精度、拼接误差、材料性能以及内外部等不同环境影响,在实际工程结构设计中,会存在各种不确定性.因此,研究混合可靠度的计算就成了关键所在.多年来,大量的研究者们对混合可靠度的分析进行了广泛的探索和研究.贺谦[2]以一阶可靠性分析为基础,使用了基于Kriging近似模型的并行子空间的多学科设计优化方法进行了多学科的综合探究;游令非[3]等基于机构运动误差分析,同时考虑了变量的模糊性和失效判据,提出了一种基于改进包络函数的模糊时变机构可靠性建模以及计算方法;姜潮[4]等对于分布概型不同以及含区间参数不确定性的可靠度计算问题提出了一种时变分析方法,有效解决了类似问题;唐忠[5]用一种偏弹性理论的全局敏感度的可靠性分析方法解决了对于机器零部件可靠性分析中存在的区间不确定性的问题;邓启程[6]等基于验算点法引入了参数不确定性和区间变量,并进行了可靠度分析研究,对可靠度指标和区间参数的不确定度关系进行了探讨;魏娟[7]等研究了基于Chebyshev包含多项式的机械手区间运动精度可靠性,并基于机构可靠性分析方法和区间不确定性模型,对空间机械手的运动精度可靠性进行了计算和评估;姜潮[8]等对于实际工程问题中的变量相关性问题,提出了一种概率区间模型,并有效解决了该问题;刘海波[9]将结构体系一部分样本信息充足的不确定变量用随机变量进行描述而另一部分样本缺乏的用区间表示,提出了一种新的含概率与区间混合的不确定性可靠性分析方法.通过学习,发现粒子群算法和增广拉格朗日乘子法的混合算法具有良好的稳定性和收敛性.
基于此,本文提出一种基于粒子群算法和增广拉格朗日乘子法的混合可靠性分析方法,该方法通过引入参数的不确定性和区间变量构造不确定模型来研究实际结构中的混合结构可靠性分析问题.该方法在一定程度的参数不确定性影响下解决具有一定非线性程度结构功能函数的可靠度指标求解和极限状态函数的收敛性问题,并通过数值算例和工程实例验证了所提方法在结构混合可靠性分析中的稳定性和有效性.
1 本文算法介绍及可靠度指标的建立
1.1 粒子群算法
粒子群算法是一种通过不断迭代找到最优解的智能算法.该算法中粒子在每一次迭代过程中通过跟踪个体极值和全局极值来更新自己.个体极值是粒子本身所找到的最优值;全局极值是整个种群目前找到的最优值.每一个粒子有自己的飞行经验,然后通过群体的飞行经验继续优化自己的飞行路线,最后在最优点靠拢.每一个粒子通过以下的算法更新自身的位置和速度.
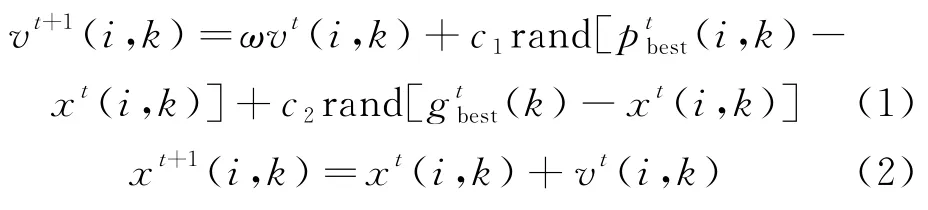
式中,i表示第i个粒子;k表示粒子所在空间点的第k个坐标分量;上标t表示第t次迭代;ω表示惯性权重;c1,c2表示加速常量;rand表示随机函数,取值为0~1;ω取值范围为0.1~0.9;c1,c2取值范围为1~2.
粒子群算法具有自起步的特点,因此在进行Matlab编程时可以先按设定的粒子群数量和坐标维数随机赋值初始化,也可以在变量预定的取值范围内随机取值.粒子群算法的流程图如图1所示.
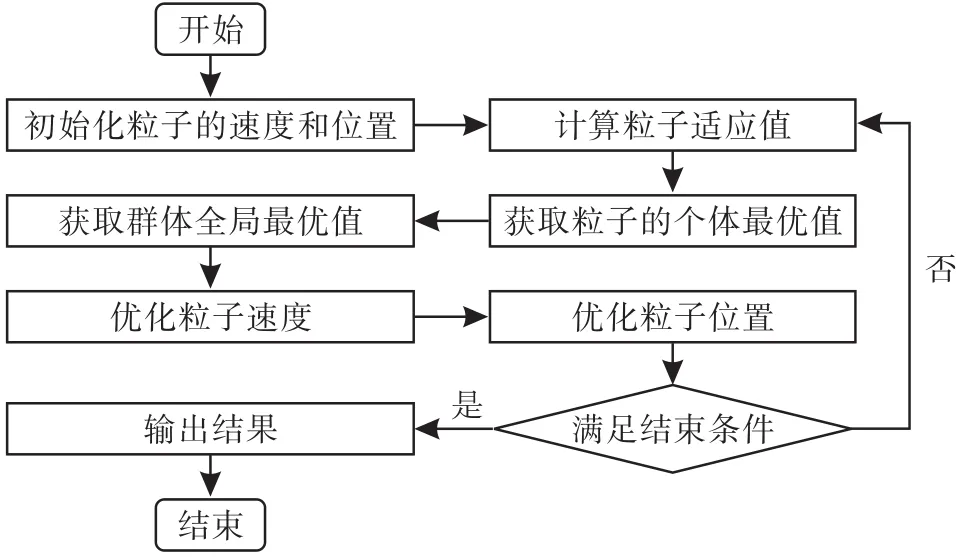
图1 粒子群算法流程图
1.2 增广拉格朗日乘子法
拉格朗日乘子法与罚函数法相结合,将有约束目标函数转化为无约束目标函数的方法,即为增广乘子法.其对约束条件既引入乘子项又引入惩罚项.根据约束条件的性质,又分为3种增广乘子法,分别为等式约束、不等式约束及混合约束的增广乘子法.
对于等式约束建立优化设计问题的数学模型:
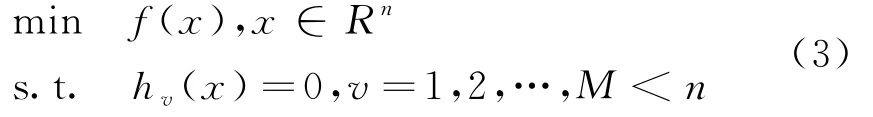
将式中的等式约束同时用罚函数法及拉格朗日乘子法构造无约束函数,则得到的拉格朗日增广函数为:
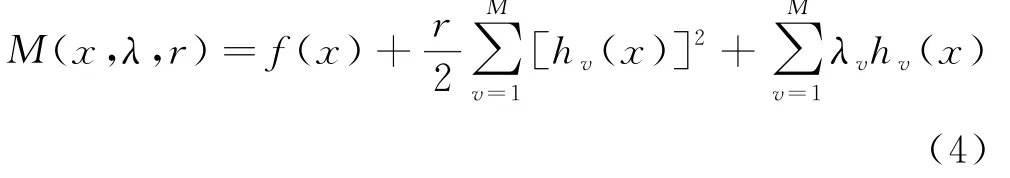
对于不等式约束建立优化设计问题的数学模型:
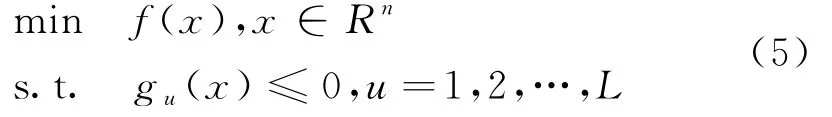
引入松弛变量y=[y1y2…y L]T,将上述不等式约束问题转化为如下的等式约束问题:根据等式约束增广乘子函数式的构造形式,构造上式增广乘子函数,形式为:
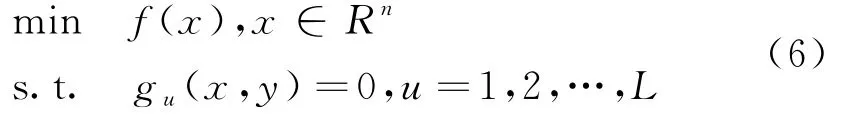
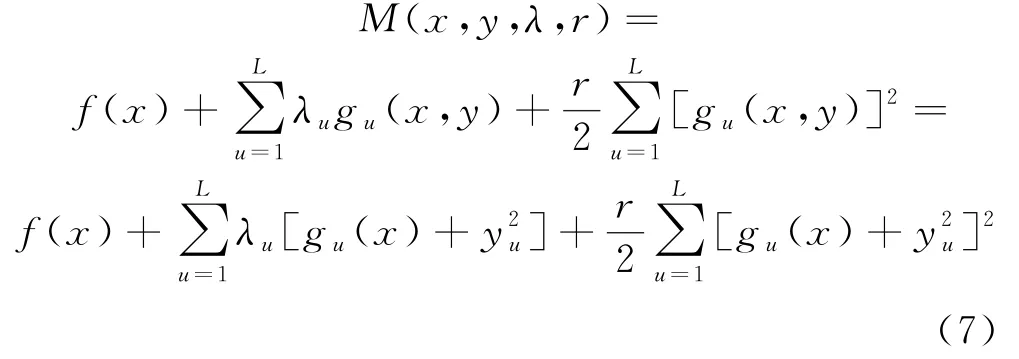
1.3 建立可靠度指标数学模型
设结构的极限状态方程为Z=g(X1,X2,…,X n)=0,其中X1,X2,…,X n为结构设计中的n个任意分布的独立随机变量.采用R-F(拉科维茨-菲斯莱法)将非正态变量当量正态化,获取均值σ'xi,标准差μ'
xi,可靠度指标β等正态分布的变量.
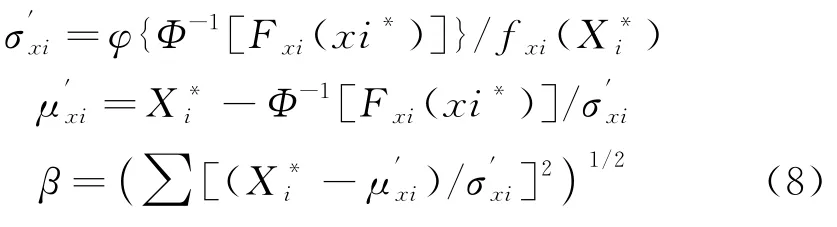
最初设计点未知,将β看做极限状态曲面上点P(X1,X2,…,X n)的函数,经过计算,找到β的最小值,即为可靠度指标值和设计点.可以建立下列约束优化模型计算可靠度指标:
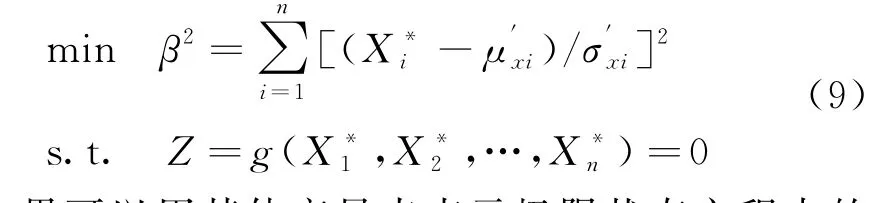
如果可以用其他变量来表示极限状态方程中的某个变量,则X j=g'(X1,X2,…,X j-1,X j+1,…,X n),则上式可转为无约束优化模型:
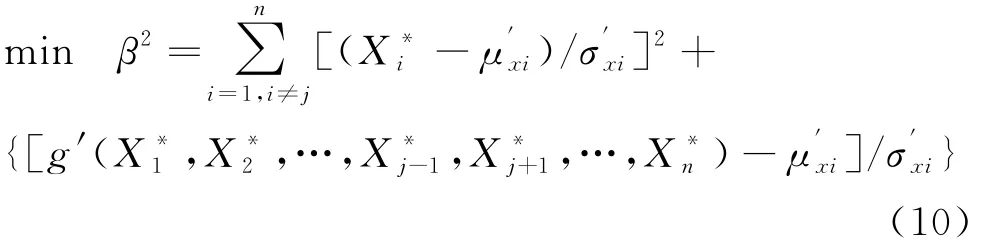
2 可靠度算例
2.1 数值算例
极限状态方程:
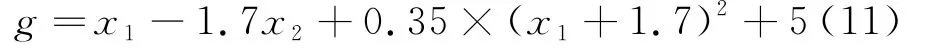
x1与x2相互独立,且均服从标准正态分布.根据上述的极限状态方程,使用本文算法得到的详细迭代数据见表1,使用一次二阶矩法得到的详细迭代数据见表2.
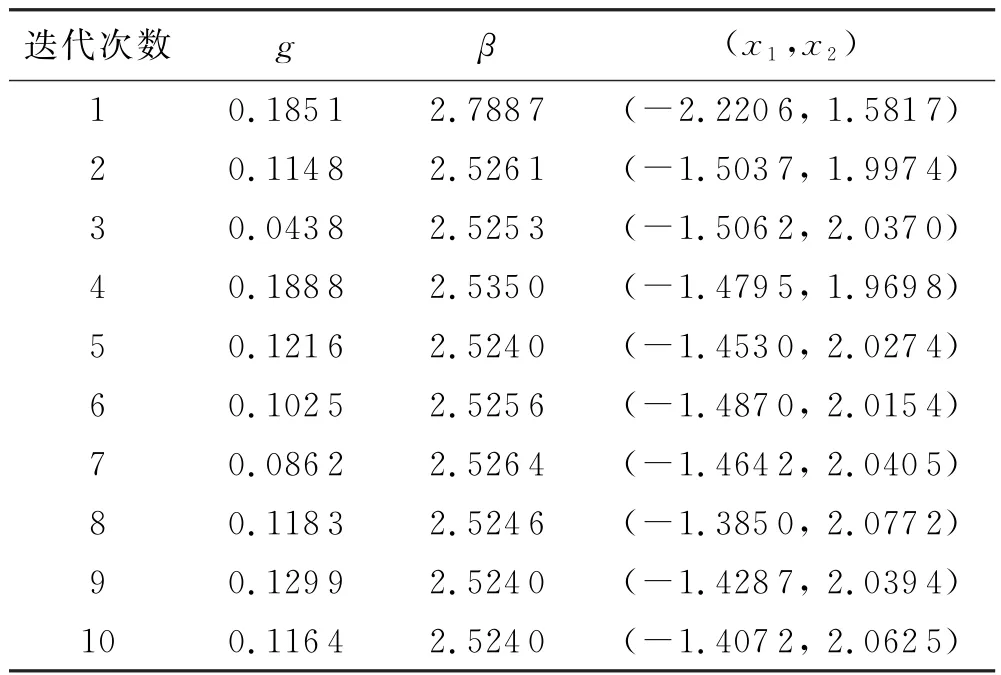
表1 本文算法计算结果
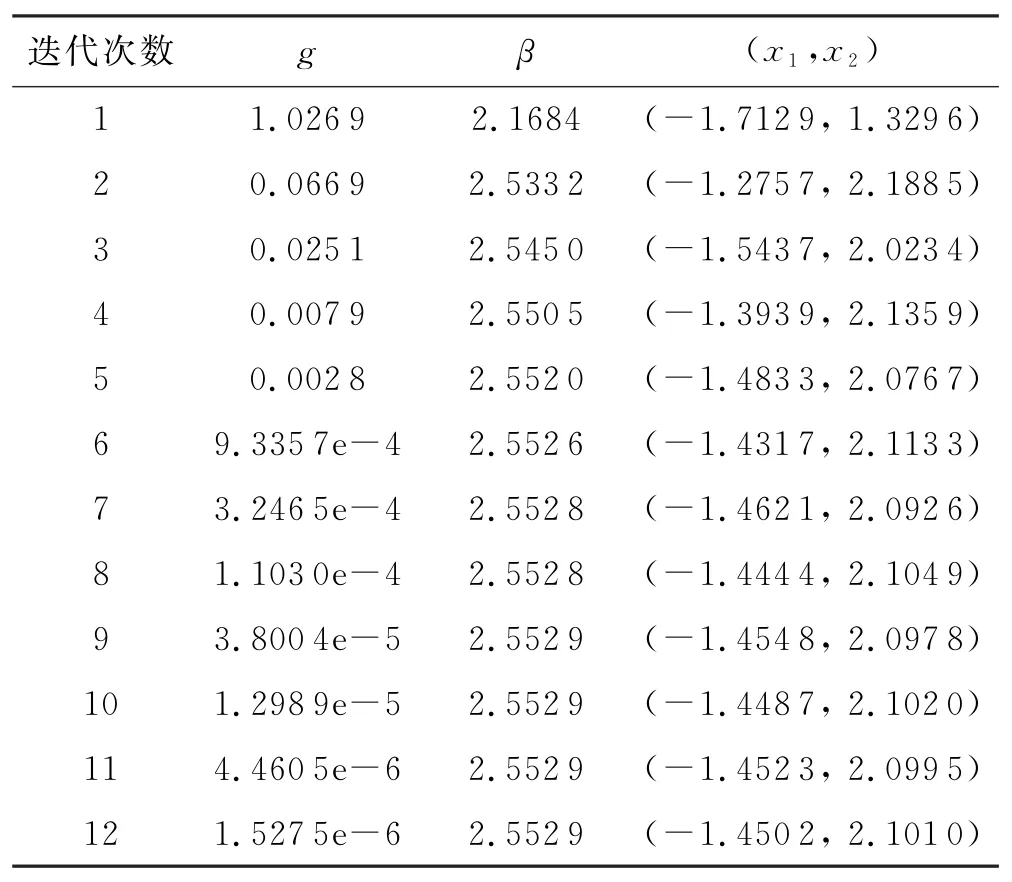
表2 一次二阶矩法迭代计算结果
可以看到,本文方法所得数值与一次二阶矩法的计算结果大致相同,证明了本文方法的可行性.同时本文算法迭代10步就可得到可靠性指标,而一次二阶矩法则需要12步才能得到结果,因此本文方法的效率更高,缩短了计算时间和工作量,所以本文算法更优.
一次二阶矩法所得可靠度指标结果见表3,迭代过程如图2所示.本文方法所得到可靠度指标结果见表4,迭代过程如图3所示.

表3 一次二阶矩法可靠性指标计算结果

表4 本文方法可靠指标计算结果
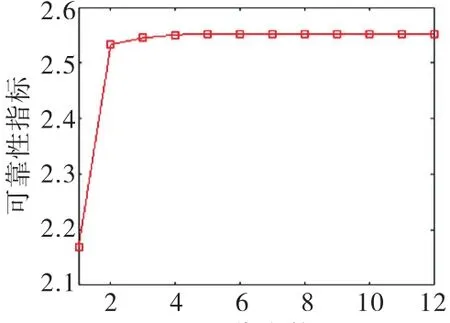
图2 一次二阶矩法迭代图
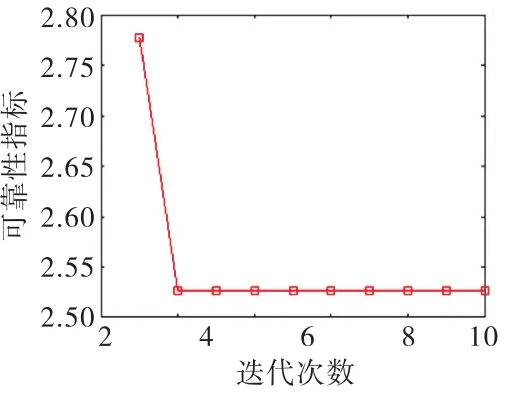
图3 本文算法迭代图
由上表数据可以看到,本文方法所得可靠性指标为2.524 0,一次二阶矩法得到的可靠性指标为2.552 9,二者结果大致相同.从迭代图上可以看到,本文算法可以快速获得稳定的结果,验证了该算法的可行性.
2.2 工程算例
1)悬臂梁算例
如图4所示,悬臂梁[10]长度为L,横截面宽度为b,高度为h,悬臂梁顶端承受作用力为p x和p y,材料的许用应力S=235 MP.悬臂梁几何尺寸和外力处理为随机变量,其不确定参数取值情况见表5,其极限方程如下:
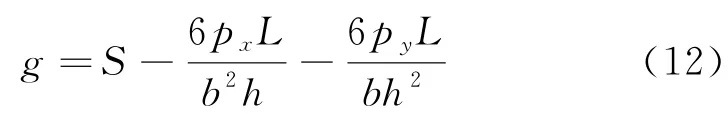
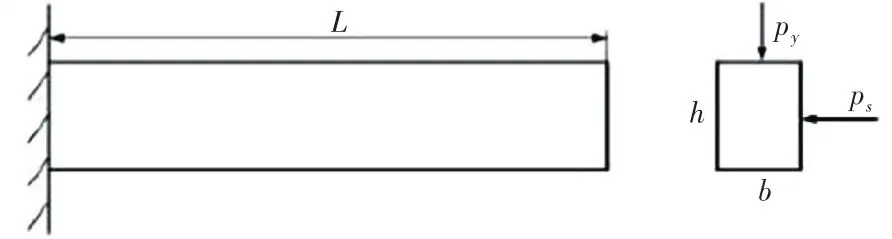
图4 悬臂梁
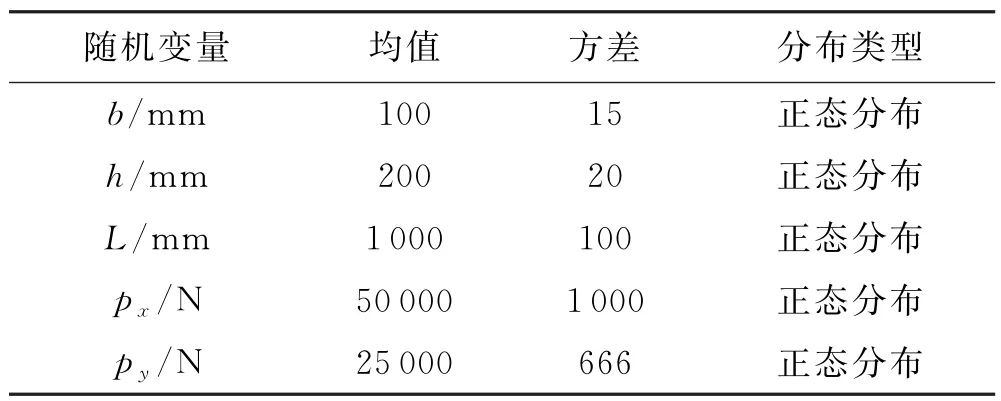
表5 不确定变量分布类型和参数取值情况
使用本文算法得出可靠度指标计算结果见表6.可知可靠性指标为β=8.077 4,失效概率Pf=2.711 9×10-15.可以看到,该悬臂梁工程算例失效概率趋近于零,表明了该算例在本文条件下具有较高的可靠性.

表6 可靠度指标计算结果
2)汽车碰撞分析
考虑如图5所示的一个车辆低速耐碰撞问题,并进行整车体系可靠性[11]分析.假设汽车发生低速偏碰撞时的速度为15 km/h,此时车辆速度较小,车辆受到碰撞的影响以车辆形变为主,车内人员受到的影响可以忽略,所以以研究车辆形变为主体,在发生低速偏碰撞时前纵梁内、外板所吸收的总能量E应小于额定值E0=500 J.变量X1~X3分别表示前保险杠厚度、吸能盒内板的厚度、吸能盒外板的厚度;变量Y1,Y2分别表示前纵梁内外板厚度.车辆有限元[12]模型如图6所示,车辆不确定参数和分布类型见表7.其极限状态方程如下:
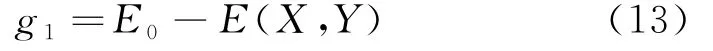
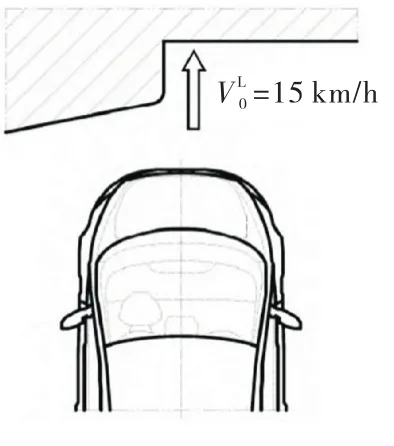
图5 低速偏置碰撞

图6 低速偏置碰撞有限元模型
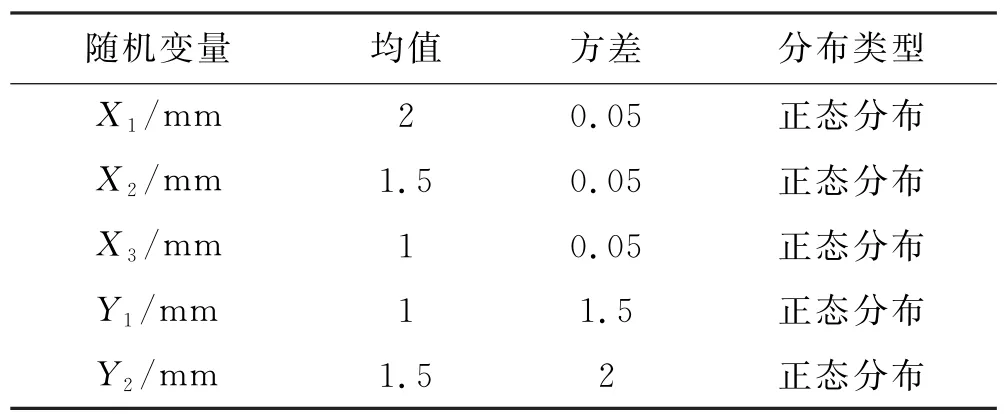
表7 不确定变量分布类型和参数取值情况
应用本文方法,通过计算可得到可靠度指标,详细计算结果见表8.同样可以看到,该汽车碰撞算例的失效概率趋近于零,表明了该算例在本文条件下具有较高的可靠性.

表8 可靠度指标计算结果
①若考虑变量的均值不确定性10%,详细参数取值情况见表9.
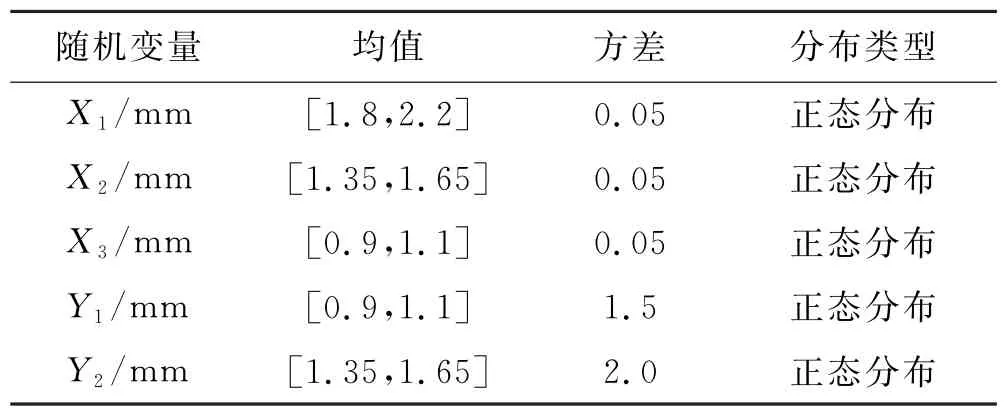
表9 各随机变量分布参数取值情况
应用本文方法,通过计算得到可靠性指标,可以看到,随着参数均值不确定度的变化,可靠度和失效概率计算结果也同样发生了变化,并且呈现正相关关系,详细计算结果见表10.
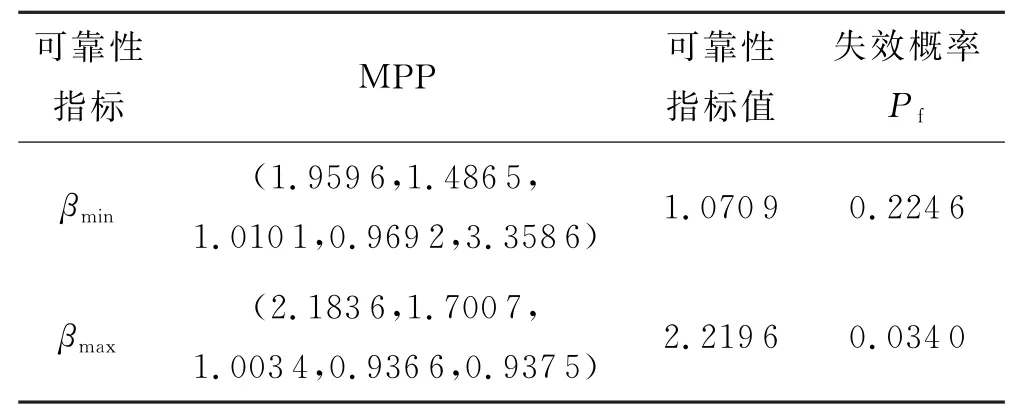
表10 可靠度指标计算结果
②若考虑变量的标准差不确定性水平40%.此时详细参数取值情况见表11.
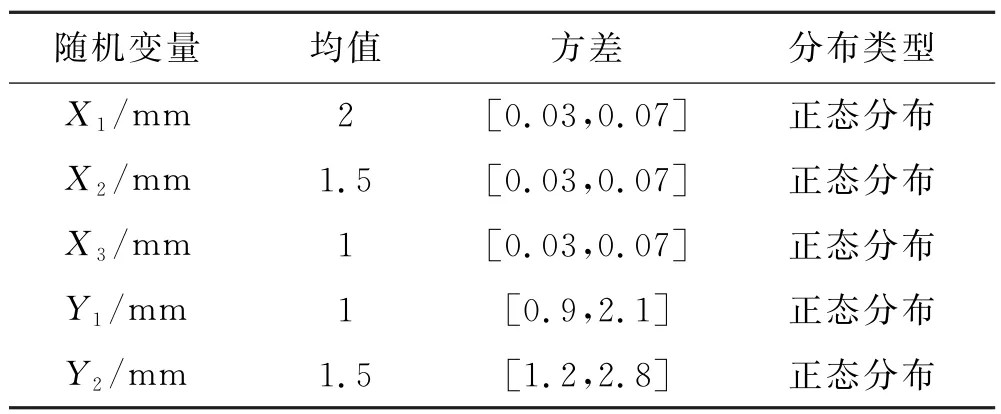
表11 各随机变量分布参数取值情况
应用本文方法,可得到可靠性指标,同样可以看到,随着参数标准差不确定度的变化,可靠度和失效概率计算结果也同样发生了变化,该变化与均值不确定度变化造成的波动相似,呈现正相关关系.详细计算结果见表12.
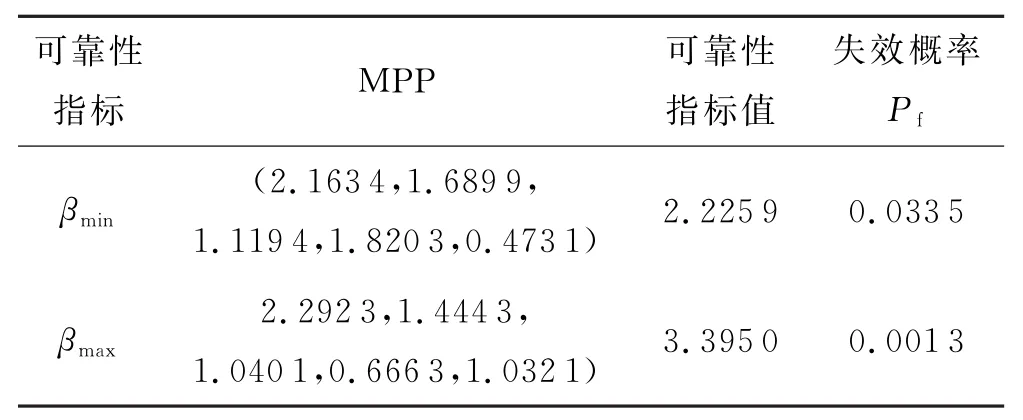
表12 可靠度指标计算结果
③若考虑变量X1~X3的均值不确定性10%,同时考虑变量Y1,Y2的标准差不确定性40%.此时详细参数取值情况见表13.
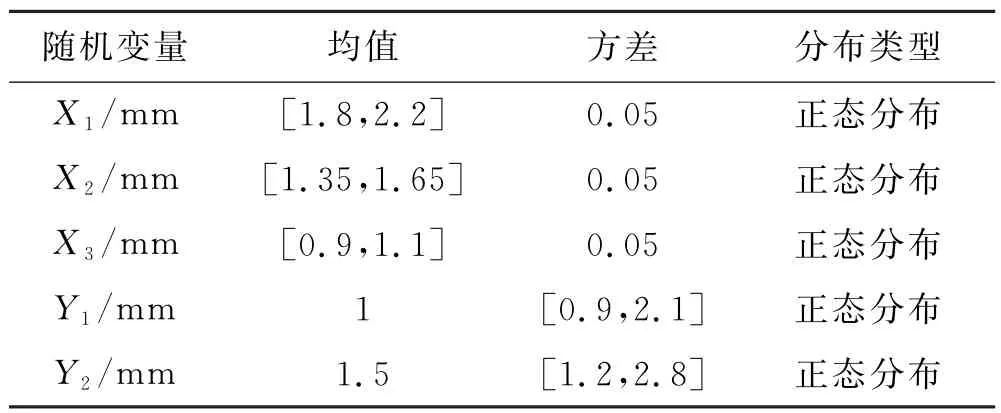
表13 各随机变量分布参数取值情况
应用本文方法,可得到可靠性指标,详细计算结果见表14.
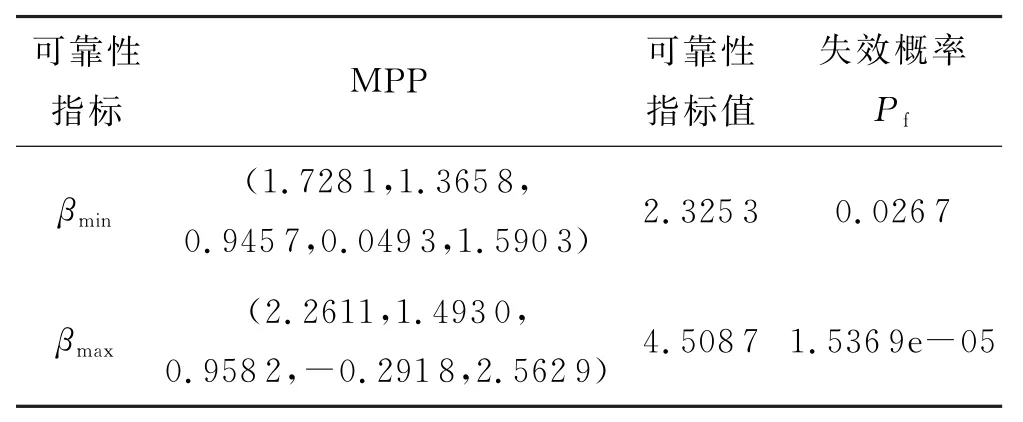
表14 可靠度指标计算结果
通过以上工程算例的计算结果表明,本文算法对于存在参数不确定度及区间变量的混合可靠度模型可靠度的计算依然有效,并能在较少的迭代步数中得到结果,缩短了时间和工作量,而且对于线性程度较高的极限状态函数,使用本文算法进行迭代计算可以得到比较精确而稳定的可靠指标,并且具有较好的收敛性;通过对不同参数不确定性的取值显示,参数不确定性对可靠度的计算会造成一定影响.
3 结 论
本文使用了1个数值算例和2个工程实例分别计算了可靠度指标,用本文算法进行计算得出结果并与使用一次二阶矩法得出的结果进行比对,所得结果与一次二阶矩算法求得的结果大致相同,验证了本文算法的可行性.该方法可用于解决具有一定非线性程度的结构功能方程、存在参数不确定度及区间变量的混合可靠度模型的可靠性分析问题.在实际工程设计中,采用此方法对结构可靠性的保证具有一定的指导意义.

