空间颜色聚类算法及其在图像特征提取中的应用

李 健, 姜 楠, 宝音巴特, 张 帆, 张伟健, 王 薇

(1.吉林农业大学 信息技术学院, 长春 130118； 2.吉林省科学技术工作者服务中心, 长春 130021；3.吉林农业大学 研究生院, 长春 130118； 4.吉林农业大学 园艺学院, 长春 130118)

图像特征提取在实际生产与生活中应用广泛, 如农业作物探测与分类、服饰行业图像检索与相关性匹配、文字文本定位识别等.但目前的图像处理方法存在许多问题, 如角点定位检测特征不明显、像素分辨率低等, 解决这些问题的有效方法是对算法进行改进、融合、目标优化等, 进而增加特征提取信息, 实现有效特征信息库的扩充, 为后续的图像处理提供更好的识别位点.图像特征提取主要分为颜色特征、形状特征、纹理特征和空间关系特征等, 不同领域特征提取的方法不同, 如Li等[1]用无监督非线性特征提取算法为高光谱图像像素的每个光谱响应曲线构建了新功能, 实现了图像的特征提取； Vaila等[2]将深度卷积神经网络与支持向量机算法融入到特征提取和分类中, 实验效果较好； Li等[3]针对图像特征的提取和识别, 提出了一种基于Gauss-Bernoulli的卷积深度信念网络, 利用卷积层的优势提取图像中的特征点； 蔡则苏等[4]提出结合K近邻分类算法提取图像多维特征， 完成了人脸表情的特征提取和识别.目前, 随着深度学习、卷积神经网络、聚类分类等算法的发展, 单一算法已无法满足实际图像的处理需求, 因此涌现了许多融合算法与改进算法.

本文主要对随机图像的颜色特征提取进行探讨与实例验证.图像颜色特征提取的方法较多, 大多数是借助混合算法实现的, 其中作为量化方法之一的颜色聚类算法也逐渐应用于不同的特征研究领域, 如图像处理与检索识别的研究, 其基本思想是通过不同的聚类算法或模型组合完成基本颜色特征提取, 增加提取信息和位点的可靠性.Shen等[5]通过使用空间聚类(DBSCAN)算法, 提出了一种实时的基于密度且带有噪声的应用程序, 实现图像超像素分割； Zhao等[6]提出了一种用于图像分割的多目标空间模糊聚类算法, 可对嘈杂图像进行高效分割； Sudip等[7]针对医学磁共振成像(MRI)变异和噪声的处理问题, 提出了用基于模糊C均值聚类算法减少数据中噪声和强度不均匀性的敏感性程度.

本文将RGB(red,green,blue)图像进行HSV(hue,saturation,value)空间转换, 分别进行R,G,B和H,S,V不同方向的直方图对比, 并借助均衡化原理将空间转换后的HSV图像进行均衡化处理, 利用均衡化后的增强图像进行K-means颜色聚类, 最终实现增强像素强度, 增加提取信息, 获取高可靠性特征数据样本的目标.

1 图像预处理

1.1 RGB图像直方图

人类肉眼识别的图像一般以RGB模式的真彩图像呈现, 并分别以R,G,B三个方向上的分量进行分向表示, 理论上可排列出224种颜色分布, 且每个像素分量可被赋值于[0,255]内的数值, 并用于表示亮度.在进行图像颜色特征提取时, 颜色直方图是一种基础的提取方法, 直方图的统计数值可反映颜色数量或基本色调的特征与频数分布信息, 且可根据空间关系将图像直方图简单归纳为全局颜色直方图、累加颜色直方图、主色调直方图等几种统计方法, 对常用的RGB颜色空间, 本文以一幅动物图像为例, 选取RGB颜色直方图进行图像初期的分量表达, 并利用MATLAB编程软件实现, 如图1所示.

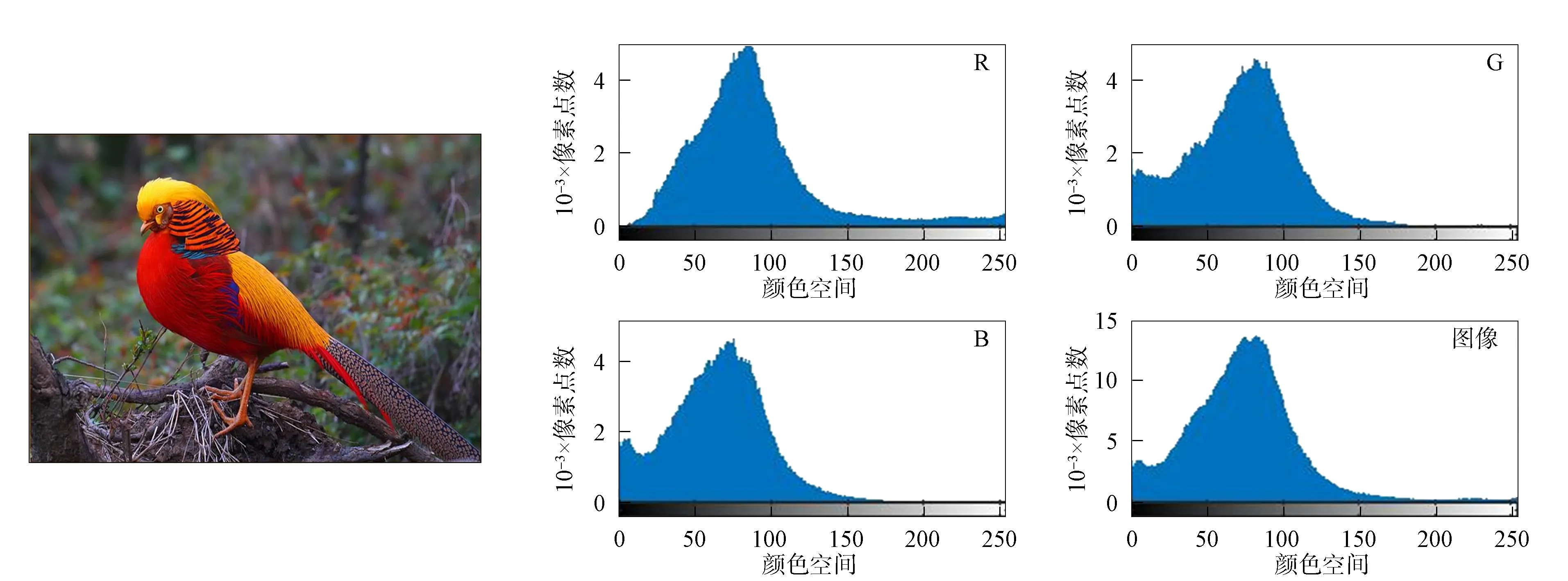
图1 RGB颜色直方图表达Fig.1 RGB color histogram expression

由图1可见, 原图像的R,G,B三个分量上的表达多集中在0～100内的区度值, 图像横轴靠右部分色彩出现饱和状态, 且无渐变趋势.在实际分析图像特征分布与信息提取过程中, 简单的运用其中单一RGB颜色直方图表示目标对象的颜色特征信息是不充分的, 一般情况下, RGB图像分量无法诠释图像的具体空间像素与位点信息的分布情况, 针对这种现象, 需将初始目标对象进行HSV空间转换.

1.2 HSV空间转换

HSV是对色彩空间的一种识别方法[8], 主要由色相(H)、饱和度(S)和明度(V) 3个方向的分量表示, 由166个空间区域组成, 其中饱和度与明度的取值范围均为[0,1], 色相的取值范围为[0,2π], 最终表示的HSV颜色空间模型是面向用户对象的一种表征[9].HSV颜色空间模型由于其与图像的色彩基础信息并无绝对相关关系, 可弥补RGB颜色空间不均匀的现象, 更符合人的视觉感知内容, 因此在图像处理过程中, 应最大程度化地将RGB颜色空间的色彩信息映射到HSV颜色空间内[10-11].RGB与HSV颜色空间互转的实现过程[12]为

(1)

V=max.

在RGB图像中, 三通道取值范围为[0,255], 需利用式(1)进行HSV空间转换, 然后采取HSV归一化处理[13], 以便数理统计阶段使用.在HSV模型中, 所有颜色分量均可用HSV圆柱坐标体系表示, 并用旋转角给定转换公式, 其中红色给定0°, 黄色给定60°, 绿色每圈给定120°, 青色给定180°, 蓝色每圈给定240°, 洋红给定300°, 且不同颜色与其补色相差180°.此外, HSV圆锥体的形状随V值的变化而变化[14-16].针对转换公式, 将初始RGB图像进行HSV转换, 得到转换后的HSV分量图与分量直方图如图2所示.

图2 HSV分量及其直方图Fig.2 HSV components and their histograms

由图2可见, 此时3个方向分量的直方图取值均在[0,1]内, 对于S和V分量直方图, 其分量峰值出现在[0.2,0.5]内的概率较大, 且对于分量值细化后的HSV颜色直方图结果更细腻.利用空间转换后的HSV图像再次进行图像的预处理工作实现对比过程, 即图像均衡化, 可消除图像分布不均匀的弊端[17].

1.3 直方图均衡化

直方图是图像空间处理与转换对比的基础方法之一, 常应用于图像亮度增强.直方图均衡化的目标是增强图像的视觉质量效果, 均衡化直方图可克服初始颜色直方图亮度不均等缺点, 因此, 对空间转换后的HSV图像进行直方图均衡化可较好地增强亮度并去除杂率[18].直方图均衡化实质是进行非线性拉伸变化后复配图像象元值得到的[19-20], 计算方法如下.

设H={X(i,j)}为初始图像的L离散灰度集合, 以{X0,X1,…,XL-1}子集进行填充,X(i,j)表示每个像素点的位置, 定义起始函数f(xk)为

(2)

其中:n表示输入起始图像示例.由概率密度函数重定累积密度函数为

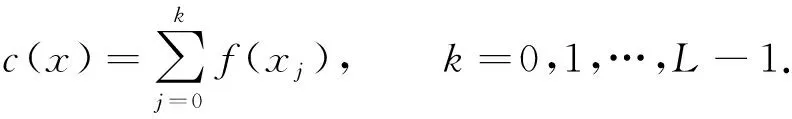
(3)

定义c(XL-1)=1, 将累积密度函数视为互转函数进行变换, 得

q(x)=X0+(XL-1-X0)c(x).

变换后的均衡化直方图为Y={Y(i,j)}, 进行q(x)表达为

Y=q(x)={q(X(i,j))|∀X(i,j)∈X}.

(4)

利用上述直方图均衡化公式处理HSV图像与分量直方图, 得到HSV均衡化后的直方图如图3所示.

图3 均衡化对比图像Fig.3 Equalization comparison image

将HSV空间变换后的图像作为二次初始输入图像使用, 最终借助MATLAB软件实现图像的输出.针对第一次空间变换后的图像, 均衡化处理在颜色的亮度上明显增强.HSV图像直方图均衡化处理结果如图4所示.由图4可见, 均衡化后的直方图在像素灰度值范围上有明显的动态波动, 且达到了实际图像对比度的一次增强效果, 同时实现了原始直方图像素比例份额压缩的增强效果[21].

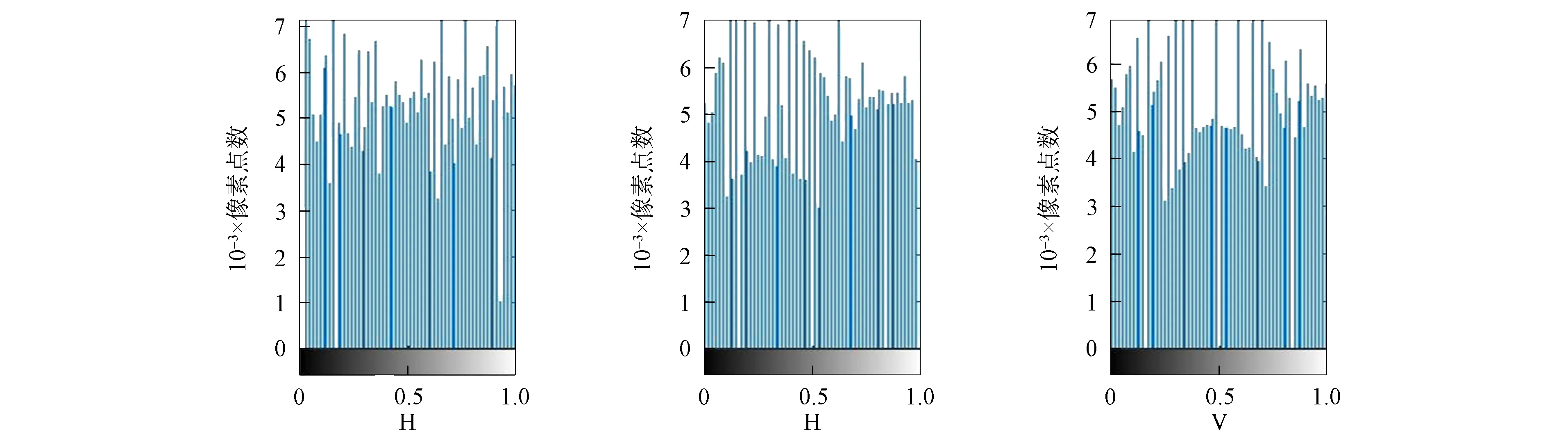
图4 HSV图像直方图均衡化处理结果Fig.4 Histogram equalization processing results of HSV image

2 颜色聚类算法的实现

对HSV图像二次增强后的效果在均衡化直方图的表现上虽有变化, 但部分颜色编码区仍有对比度滞留问题, 因此本文继续采用融入rgb2ind函数方法的K-means聚类算法将均衡化后的图像进行聚类增强, 以达到在饱和度方向上的明显增强效果.K-means算法的颜色聚类过程由聚类中心进行类别表示, 以聚类三维散点图中的不同颜色标记不同方向的聚类分层.

K-means算法是一种距离聚类方法, 利用靠近目标对象距离的远近进行分类估算, 具有运行效率高和可伸缩性较好的特点.融入rgb2ind函数的K-means聚类算法在处理图像颜色方面具有较高的处理效率和表达效果[22-24].聚类开始需要初置随机质心点, 计算每个散点与质心点间的欧氏距离进而形成簇, 重新计算m个簇的中心质点, 然后根据相似性原则进行重复迭代[25-26].其算法实现过程如下：

(5)

其中:d为定义的欧氏距离公式;xi为实数, 表示x的第i个坐标；yi为实数, 表示y的第i个坐标.上述公式为n维空间的欧氏距离.

借助欧氏距离的计算过程, 根据每类数据点的基数容量计算均值, 最后将rgb2ind函数融入到K-means颜色聚类算法, 计算公式为

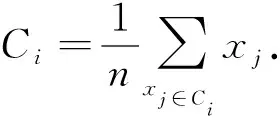
(6)

Ci的值是簇中心不变的取值, 所有的xj∈Ci, 则有最小值公式为

(7)

其中k表示中心簇的数量.

3 结果对比

原始彩色RGB图像经过HSV分量直方图转换后, 其转换图像在色相、饱和度和明度三个方向上的分量已进行了一次增强效果的表示, 数据增强与分布结果列于表1.由表1可见, 在初始HSV分量直方图内峰值数据区间为[4 000,5 000], 其峰值分布区间多为[0,0.5], 而经过均衡化后的HSV分量直方图的色相、饱和度与明度数据峰值出现区间均有不同程度的扩增, 此外其峰值数据分布横向区间也有明显增加趋势, 因此, HSV图像均衡化直方图的处理可有效增加原始彩色RGB图像像素的明度、亮度与饱和度等观测值, 进而实现增强图像特征信息提取的目的.

表1 HSV分量直方图与均衡化直方图的数据分布

图5 均衡聚类及其三维空间颜色图Fig.5 Equilibrium clustering and its three-dimensional color map

根据均值聚类理论, 绘制HSV图像与均衡化HSV图像的空间颜色三维图, 融入rgb2ind函数的K-means算法的颜色聚类对比结果如图5所示.由图5可见, 共有2行3列的数据样图, 第一行表示经过HSV空间变换的HSV一次增强图像的聚类图及其相关三维空间颜色群集分类散点图； 第二行表示经过均衡化二次增强效果的颜色聚类及其空间三维散点图的分布情况.由二者的对比结果可见, 经过均衡化处理的HSV空间图像在K-means均值聚类运算中, 呈现出对比度增强、颜色簇增多的现象, 且分类集存在大量的颜色特征扩充情形.而二次初始HSV图像在进行空间颜色聚类后, 在颜色分布的数量上与明亮度方向, 均处于特征不明显状态, 且颜色空间的分布差异性较大, 未形成较明亮的颜色层或颜色簇.因此, 融入rgb2ind函数的K-means均值颜色聚类对二次均衡化处理后的图像有更明显的图像颜色特征, 也可提供更多的特征点与特征信息.

综上所述, 本文针对目前图像基本颜色单一、可供信息不足的问题, 提出了一种改进的空间颜色聚类算法.实验结果表明, 经过均衡化处理后的图像可利用融入rgb2ind函数的K-means算法实现颜色对比度的增强和特征集的扩充, 在实际应用中, 可利用该方法实现随机图像特征信息的二次增强和多级提取, 为模糊不清的图像提供了一种基于颜色特征提取的增强方法.对非均衡化的HSV空间转换图像进行验证对比的结果表明, 均衡化后的HSV图像在颜色聚类方法的处理下, 其颜色特征表现更明显.