遥感卫星地面站资源调度的混合分解算法

刘静怡, 田妙苗, 黄 鹏, 林友明, 马广彬

(1.中国科学院 遥感与数字地球研究所, 北京 100094；2.中国科学院大学 电子电气与通信工程学院, 北京 100049)

卫星获取遥感数据后, 需将这些数据传输到地面系统, 由地面站完成数据的接收与记录.遥感卫星地面站(下称地面站)资源调度是指考虑时间窗口和资源性能等约束, 合理分配地面站资源, 以完成遥感卫星数据接收任务的过程.随着遥感在各领域中的广泛应用[1], 数据接收任务日益增多, 调度场景更复杂, 导致资源调度规模增大, 求解难度上升, 对求解地面站资源调度问题提出了更高的要求, 因此, 快速、高效地调度地面站资源, 最优化接收卫星数据, 成为一个亟待解决的问题[2].

地面站资源调度问题是一个复杂的组合优化问题[3], 求解算法包括确定性算法、智能搜索算法、启发式算法及混合算法[4-8].近年来, 针对地面站的资源调度效率、资源使用率、任务完成率等问题已提出了许多求解算法.文献[9]针对伽利略系统严格的分发要求提出了一种新的上行调度算法, 有效提高了资源利用率; 文献[10-11]研究了蚁群算法在地面站资源调度问题中的应用, 并对算法进行了改进, 提高了算法的搜索能力; 为进一步提高求解的效率和精度, 文献[12-13]使用混合求解算法对组合优化问题进行求解, 通过对问题分解, 获得了良好的求解效果.中国遥感卫星地面站采用遗传算法求解该问题时, 为加快求解速度, 基于分治法思想先将待解问题按冲突任务集分解为多个小任务量的子问题.但随着数据接收任务数量和任务间冲突的增加, 冲突任务集规模增大, 这种分解的作用会越来越有限.因此, 本文基于中国遥感卫星地面站运行管理的现实需求, 以提高地面站资源调度时效性为目标, 对多地面站资源调度问题进行研究.考虑卫星数据接收任务优先级、时间窗口和地面站资源性能等约束条件, 建立基于连续时间的混合整数线性规划(mixed integer linear programming, MILP)模型.为加快求解速度, 将地面站资源调度问题分为地面站选择和单地面站资源调度两层, 提出一种基于启发式规则和设备分解的混合分解算法.该算法首先利用先验信息, 对地面站资源使用的冲突程度进行评价, 根据评价值选择接收任务的地面站, 将地面站资源调度问题分解为多个单地面站资源调度问题； 然后使用Lagrange分解算法, 松弛站内天线与记录器关联约束, 按设备进行分解, 进一步缩小问题规模, 对天线调度与记录器调度子问题分别求解, 得到问题的可行解.

1 地面站资源调度问题

卫星数据接收设备主要包括天线、信道、记录器等, 接收过程如图1(A)所示.数据由天线接收后, 经过信道的变频和解调, 最后由记录器记录.当遥感卫星进入地面站接收范围时, 地面站可对卫星数据进行接收, 地面站能接收卫星数据的时间范围称为时间窗口.由于地面站的信道资源相对充足, 因此本文只考虑天线和记录器的调度问题.

在地面站接收卫星数据过程中, 存在接收任务重叠和接收资源冲突两个问题.

1.1 接收任务重叠

对于采用广播方式发送信号的卫星, 当其位于多个地面站接收范围间的重叠区域时, 每个地面站均可接收到该卫星的数据.对部分任务数据重复接收的情形称为接收任务重叠, 如图1(B)所示.由图1(B)可见, 任务a,b,c分别表示地面站1,2,3对同一卫星的数据接收任务.任务a和b称为一组重叠任务,t2～t3为其重叠时间； 任务b和c为一组存在包含关系的重叠任务,t3～t4为其重叠时间.对于重叠任务, 为减少或避免重复接收、浪费地面站资源, 需选择尽可能少的接收地面站承担任务, 同时为了保证数据接收质量, 在实际运行中, 两重叠任务之间需保证一定长度的重叠时间.

图1 卫星数据接收过程Fig.1 Receiving process of satellite data

1.2 接收资源冲突

当多个卫星同时经过同一地面站的接收范围时, 如果同一时刻的卫星任务数量大于接收站天线数量, 或下传数据量超出记录器能力范围, 就会导致部分任务数据无法被接收, 即接收资源冲突.这种情形下, 地面站资源调度需考虑天线、记录器的性能及任务的重要性等因素.

2 问题模型及求解算法

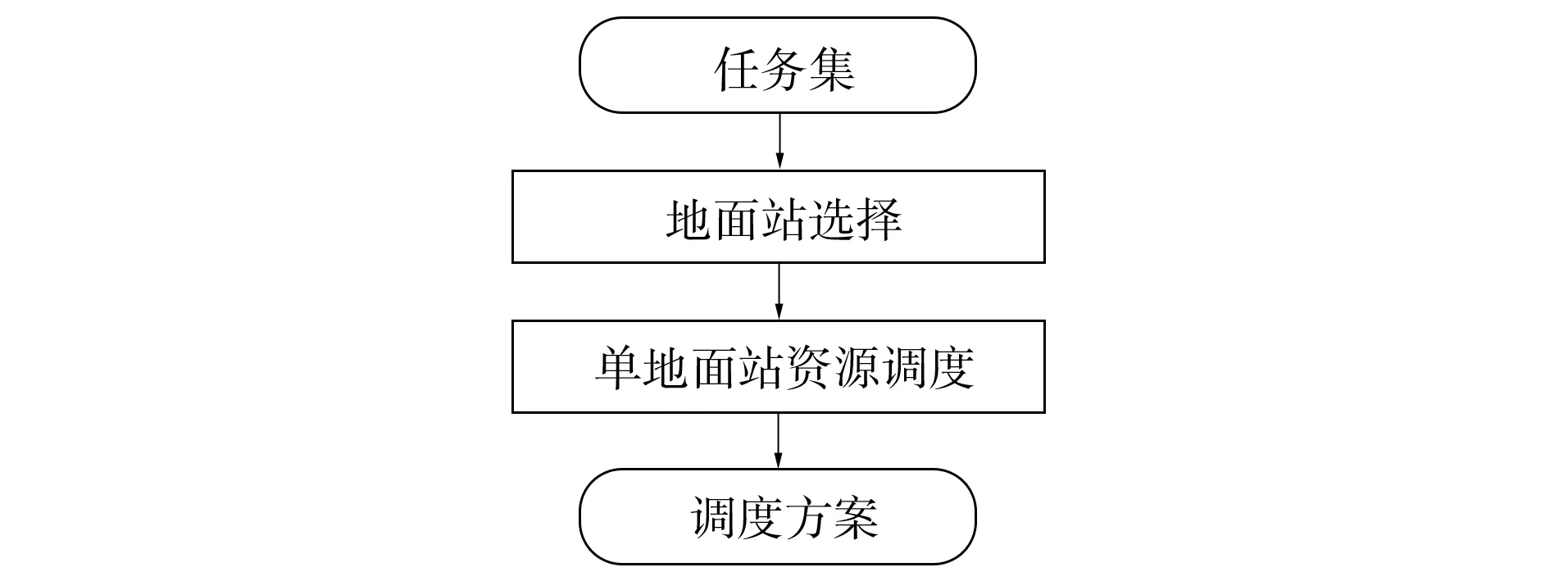
图2 求解算法流程Fig.2 Flow chart of solution algorithm

对于重叠任务, 需综合考虑重叠时间内多个地面站中资源的使用情形； 对已确定接收地面站的任务, 需对该地面站的站内资源进行调度.针对上述问题, 本文将求解地面站的资源调度问题分为两个阶段.第一阶段, 为重叠任务分配地面站, 将多地面站调度问题转化为多个单地面站调度问题.第二阶段, 对单个地面站的站内资源进行调度, 为任务分配具体设备资源.求解流程如图2所示.

2.1 地面站选择

地面站选择的目标是确定重叠任务的接收地面站, 尽量多地接收卫星数据.考虑到地面站接收卫星数据时的设备切换成本, 在实际操作中通常不接收被包含的任务(如图1(B)中任务c被任务b包含, 取消地面站3对任务c的接收).本文提出一种考虑地面站资源数的地面站资源使用冲突程度评价指标(简称评价指标), 并根据该指标获得地面站选择的近似最优方案.该评价指标为重叠时间内地面站接收任务数量与地面站资源数量的比值, 公式为

(1)

其中：i为卫星数据接收任务序号;s为地面站; clushnum(i,s)表示在任务i的重叠时间内地面站s接收卫星任务的数量; resource(s)表示地面站s的资源数量;Io为重叠任务的集合;S为地面站集合.cd(i,s)值越小, 重叠时间内地面站资源使用冲突程度越低.

引入评价指标后, 地面站的选择可通过比较评价指标值得到.通过以下启发式规则完成对地面站的调度：

规则1) 调度的目标为最小化地面站资源冲突程度和地面站切换次数, 即

(2)

其中： station(i,s)为二值变量, 任务i由地面站s接收时为1, 否则为0; over(i,s)为地面站s接收任务i时设备的切换次数;cd(i,s)为地面站s接收任务i时的评价指标.

规则2) 一个任务最多选择一个地面站进行接收, 表示为

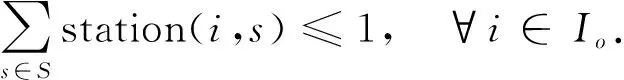
(3)

规则3) 一组重叠任务在重叠时间内至少需要选择一个地面站接收, 表示为

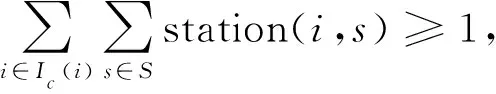
(4)

其中Ic(i)为任务i所在的重叠任务组.

算法步骤如下：

1) 对任务集I中的n个任务, 按任务开始时间从小到大的顺序排序；

2) 将任务集中的每个任务i依次与其后的每个任务比较, 如果存在与其卫星名相同、接收时间有重叠的任务i′, 则i与i′组成一组重叠任务；

3) 比较重叠任务组中任务的接收时间, 如果存在包含关系, 则删除被包含的任务, 转步骤6); 否则, 转步骤4)；

4) 根据式(1)计算评价指标；

5) 选择评价指标最大的地面站, 减少对应任务的接收时间；

6) 判断任务集I是否已经遍历结束, 若判断结果为是, 则返回地面站的选择方案； 否则转步骤2).

2.2 单地面站资源调度模型

单地面站资源调度问题的优化目标为最小化任务的接收成本.这里成本包括4部分： 天线使用成本、记录器使用成本、任务不完整接收的惩罚和记录器共用的惩罚.目标函数为

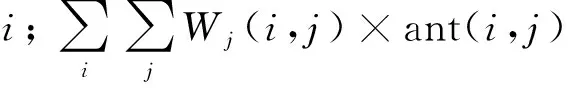
该问题的约束条件可分为以下4类： 天线分配约束、记录器分配约束、天线记录器关联约束和任务接收时间约束.

1) 天线分配约束.对每个任务, 最多分配一个天线， 表示为

(6)

其中I和J分别表示可接收任务和单地面站中天线资源的集合.

在前一个任务接收结束后一段时间τ内, 同一天线不能接收其他任务， 表示为

其中: 参数M是一个极大值; 参数τ为设备切换时间, 在该问题中τ=270 s; 变量b(i)表示任务i的接收开始时间; 变量c(i)表示接收任务结束时间;X(i,i′)为二值变量, 当其值为1时表示任务i′顺序在任务i后, 默认将任务列表按计划任务开始时间进行排序, 则X(i,i′)可表示为

当任务接收时间不为0时, 必须分配天线, 表示为

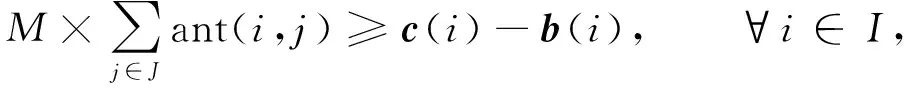
(8)

其中变量b(i)和c(i)分别是实际接收的开始时间和结束时间.

2) 记录器约束.对每个任务最多分配一个记录器, 表示为

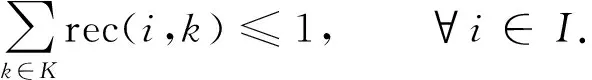
(9)

不存在记录器共用的两个任务, 在前一个任务接收结束后一段时间τ内, 同一记录器不能接收其他任务, 表示为

其中: 参数pt(i)为计划任务进行时间;y(i,i′)为一个二值变量, 当任务i与i′存在记录器共用时其值为1, 否则为0.当每个记录器在同一时间记录任务所需的通道数不得超过记录器本身具有的逻辑记录器数目时， 表示为

其中: 参数chanl(i)表示任务i数据下行通道数量； 参数logicnum(k)表示记录器k逻辑记录器数量.

3) 天线记录器关联约束.每个任务天线与记录器或者都分配或者都不分配, 表示为

(12)

4) 任务接收时间约束.任务的未接收时间表示为

pnc(i)=pt(i)-c(i)+b(i), ∀i∈I.

(13)

接收任务开始时间和结束时间必须在时间窗口内, 表示为

c(i)≤te(i), ∀i∈I,

(14)

b(i)≥st(i), ∀i∈I,

(15)

其中: 参数te(i)表示时间窗口的结束时间; 参数st(i)表示时间窗口的开始时间.接收任务开始时间小于等于接收任务结束时间表示为

b(i)≤c(i), ∀i∈I.

(16)

2.3 Lagrange分解算法

Lagrange分解基本思想是在求解有约束的数学规划模型时, 通过引入Lagrange乘子松弛部分约束, 从而将原问题分解为多个规模较小、易求解的对偶子问题.各子问题之间利用Lagrange乘子关联, 通过不断调整Lagrange乘子及求解子问题可得到原问题的近似最优解.

2.3.1 分解方案 单地面站调度模型中, 考虑对天线和记录器两类资源进行调度.由于天线和记录器的调度关系相对独立, 因此本文设计了基于设备分解的Lagrange分解方法, 通过松弛天线与记录器之间的关联约束(12), 将该问题分解成天线调度P1和记录器调度P2两个子问题.为保证所有子问题中相同任务对应的开始时间和结束时间相同, 需添加如下约束：

c1(i)=c2(i), ∀i∈I,

(17)

b1(i)=b2(i), ∀i∈I,

(18)

其中,b1(i)和c1(i)及b2(i)和c2(i)分别为子问题P1和P2的接收开始时间和结束时间.

给定非负Lagrange乘子λ1松弛约束(12)、λ2松弛约束(17)、λ3松弛约束(18), 可得如下天线调度子问题P1的数学模型：

其中: pnc1(i)为P1中任务因冲突未接收的时间; 式(19)为P1的目标函数; 式(6), 式(20)～(25)为其约束条件.记录器调度子问题P2的数学模型为

其中: pnc2(i)为P2中任务因冲突未接收的时间; 式(26)为P2的目标函数; 式(9),(11),(27)～(32)为其约束条件.

2.3.2 Lagrange乘子的更新 在单地面站资源分配问题中, Lagrange乘子λ1,λ2,λ3表示天线调度方案中任务i的天线分配数、接收开始时间、接收结束时间和记录器调度方案不一致时所带来的惩罚.因此, 当天线调度方案中任务i天线分配数、接收开始时间和接收结束时间大于记录器调度方案中对应项时,λ1,λ2,λ3增大, 反之减小.次梯度算法因其形式简单且能保证收敛的稳定性而得到广泛应用, 其表达式为

λk+1=λk+[tk/(‖Sk‖2+γ)]Sk,

(33)

其中:k表示算法的迭代次数；t为步长；S表示由子问题的解计算得到的次梯度.本文算法中, 在次梯度公式中添加了一个给定的极小值γ, 其作用是为了避免分母为0.本文算法中γ=10-5,λ1,λ2,λ3的初始值为0.

2.3.3 可行化方案 由于子问题中松弛了部分约束, 得到的解可能不是原问题的可行解.同时对于好的Lagrange乘子, 子问题解中的二值变量, 即ant(i,j)和rec(i,k)的取值接近最优解, 因此可利用一种启发式算法将不可行解转换成可行解.在启发式算法中, 如果子问题的解不满足天线记录器关联约束(12), 则将为任务分配资源较少的子问题的解作为已知量, 代入单站资源调度模型进行计算, 得到单站资源调度问题的可行解及对应的目标函数值costP.

2.3.4 停止准则 对偶间隙是衡量松弛问题和原问题解接近程度的一个指标.通常以对偶间隙的大小作为停止准则, 当对偶间隙小于给定值时停止迭代, 即

gap≤ε.

(34)

对偶间隙可表示为

gap=(costP-cost_1p-cost_2p)/costP,

(35)

其中： costP表示问题P可行解对应的目标函数值； cost_1p和cost_2p分别表示子问题P1和P2所得解对应的目标函数值.本文算法中ε=0.3.

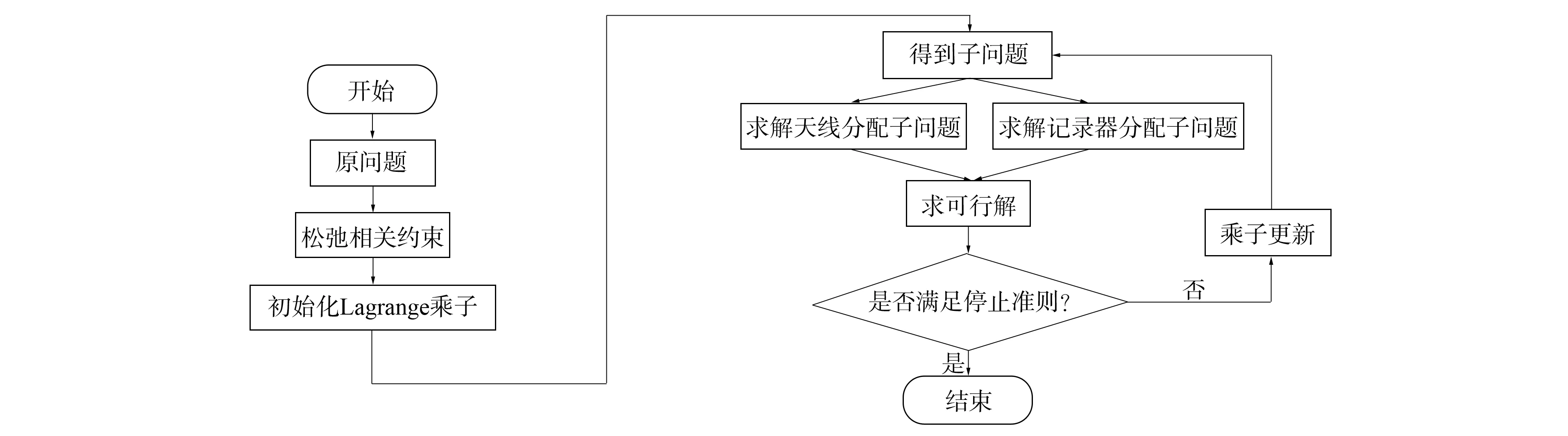
图3 Lagrange分解算法流程Fig.3 Flow chart of Lagrangean decomposition algorithm

为保证计算效率, 得到满意解时能快速输出结果, 本文算法在子问题的解满足被松弛的约束(12)、步长t→0或循环次数达到给定值时, 停止迭代.

2.3.5 算法流程 Lagrange分解算法的求解流程如图3所示, 步骤如下：

1) 初始化Lagrange乘子；

2) 求解子问题, 获得子问题的目标函数值cost_1p和cost_2p；

3) 利用启发式算法可行化子问题的解, 得到可行解对应的目标函数值costP；

4) 计算对偶间隙, 如果对偶间隙小于给定值, 或子问题的解满足被松弛的约束(12), 说明资源分配非常接近最优解, 则转步骤6)；

5) 更新Lagrange乘子, 如果步长趋于0, 或循环次数达到给定最大循环次数, 则说明资源分配不能进一步进行有效调整, 转步骤6)；

6) 输出地面站资源调度方案, 算法终止.

3 实验结果与分析

3.1 规模及参数

为验证算法的有效性和实用性, 本文选取15组不同规模的案例, 表1列出了不同实例的任务数量和任务总时长.本文考虑了3个地面站, 地面站资源列于表2, 包括天线资源和记录器资源.

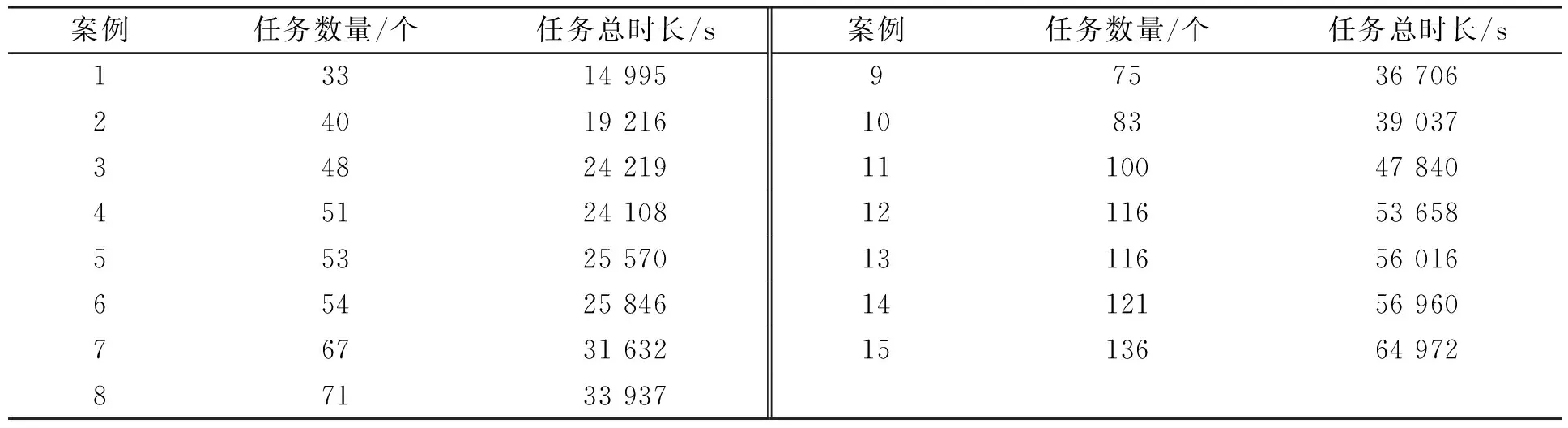
表1 案例规模

表2 地面站资源

3.2 求解时间和目标函数值

在实际运行中, 中国遥感卫星地面站采用结合启发式规则的遗传算法(下称原算法)对地面站资源进行调度.本文算法与原算法的计算结果列于表3.

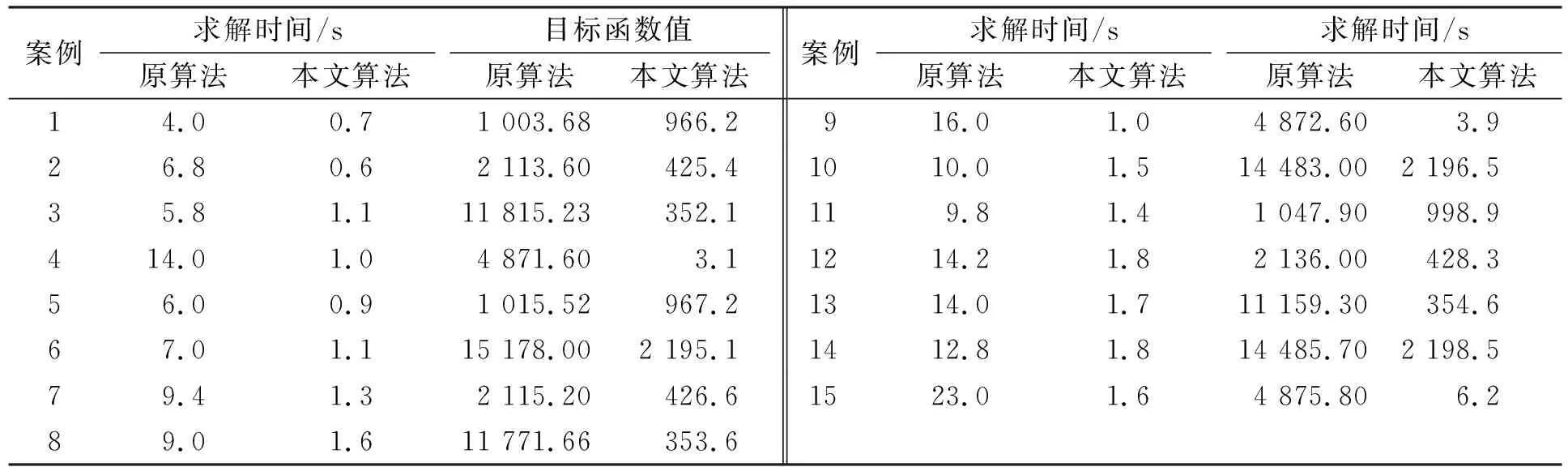
表3 本文算法与原算法的计算结果对比

表3中原算法所列结果为5次计算所得结果的平均值.由表3可见, 相比原算法, 本文算法在求解时间上提高了81%～94%； 在目标函数上, 本文算法的目标函数值均小于原算法.求解时间的减少, 说明本文算法能有效提高多地面站资源调度问题的求解效率； 目标函数的减少, 说明本文算法的资源调度方案更合理, 降低了接收成本.

3.3 典型案例分析

表4和表5分别为案例7中任务1～11及案例13中任务1～14的调度结果.包括计划接收时长、实际接收时长、天线分配和记录器分配.其中计划接收时长为任务时间窗口的长度； 实际接收时长为调度结果中任务的实际接收时长； 任务的优先级分为5级, 由高到低分别用P1～P5表示.

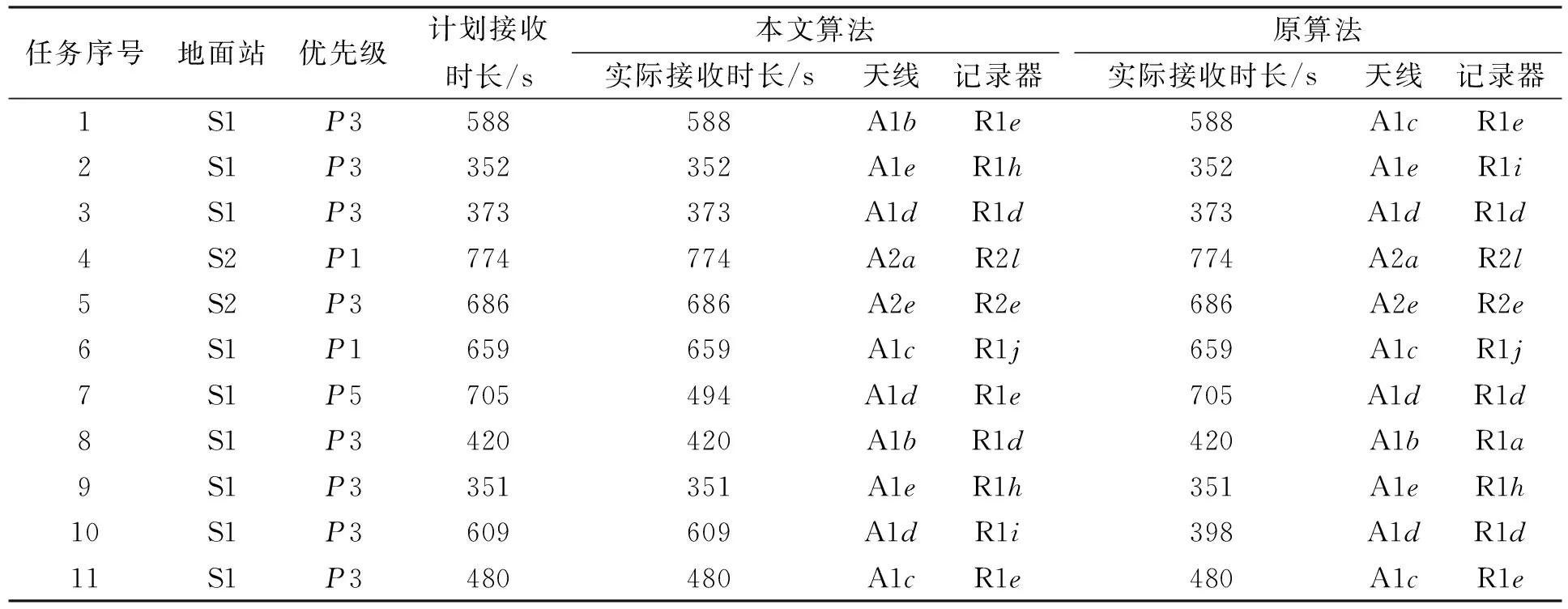
表4 案例7调度结果

由表4可见, 本文算法与原算法的调度结果中, 任务1～6、任务8～9和任务11的实际接收时长相同.对任务7和任务10, 本文算法未完整接收任务7, 未接收时间为211 s； 原算法未完整接收任务10, 未接收时间为211 s.从接收时长的角度分析, 本文算法和原算法的实际接收时长相同, 未接收任务的时长均为211 s.从任务优先级的角度分析, 任务10的优先级高于任务7, 原算法选择完整接收任务7, 本文算法选择完整接收任务10, 保证了高优先级任务的接收.因此, 两种算法的任务接收时长相同, 但考虑任务优先级, 本文算法更优.

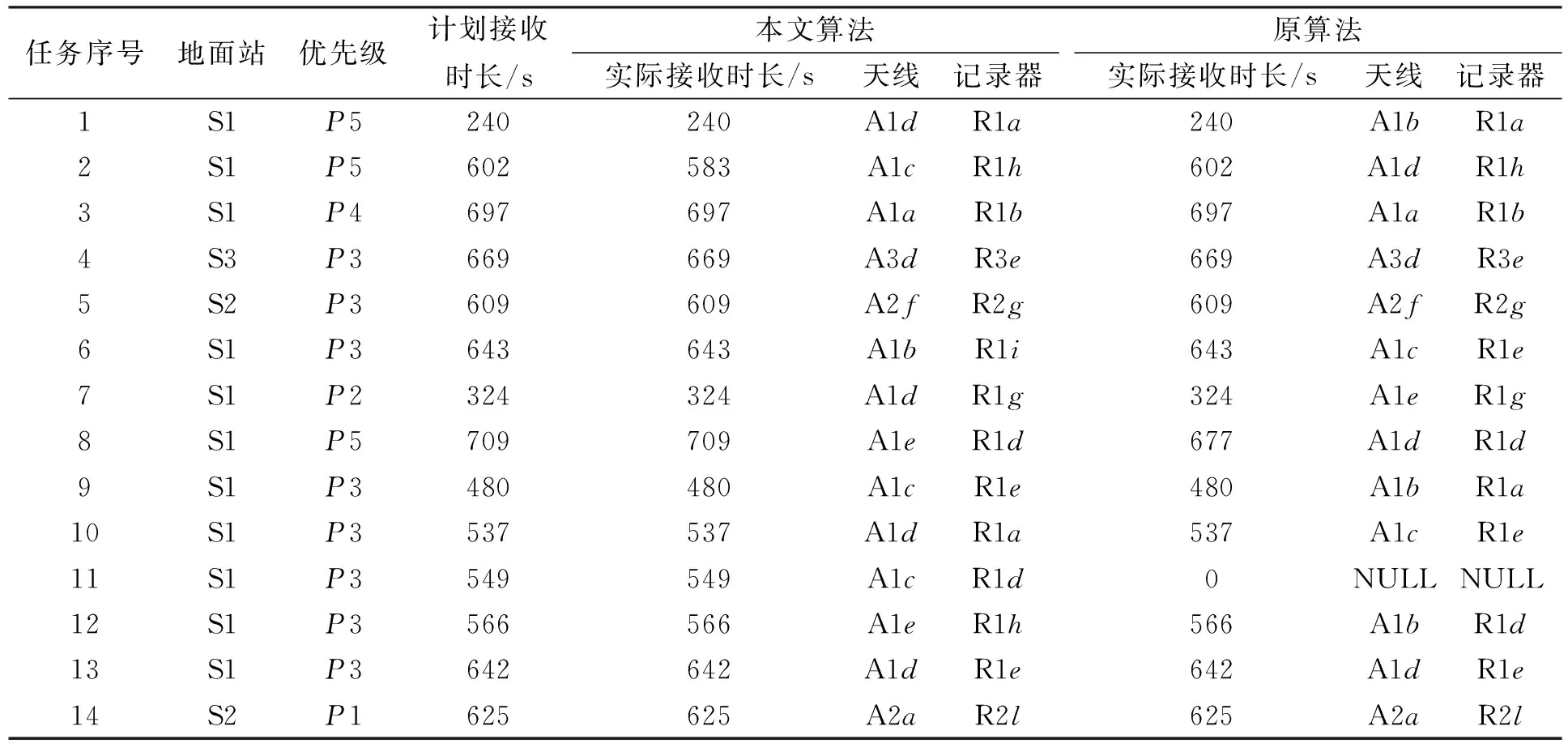
表5 案例13调度结果

由表5可见, 对比本文算法与原算法的结果, 任务1、任务3～7、任务9～10和任务12～14的实际接收时长相同.对任务2,8和11, 本文算法未完整接收任务2, 未接收时间为19 s； 原算法未完整接收任务8且未接收任务11, 未接收时间分别为32 s和549 s.从接收时长的角度分析, 本文算法实际接收时长减少19 s, 原算法减少581 s, 本文算法的实际接收时长更长, 保证了更多卫星数据的接收.从任务优先级的角度分析, 任务11的优先级高于任务2和任务8, 本文算法的调度结果完整接收任务11, 保证了高优先级任务的接收.因此, 从接收时长和任务优先级两方面评价, 本文算法结果更优.

综上所述, 针对中国遥感卫星地面站实际运行中的地面站资源调度问题变量多、规模大、难以快速求解等问题, 本文提出了一种混合分解算法.实验结果表明, 该算法提高了任务的求解效率, 在任务接收时长和高优先级任务的接收上优化效果较好.