基于多元智能理论的高中数学教学实践研究

陈素萍

【摘要】多元智能理论重在对学生综合素质与能力的培养，强调学生对数学知识的理解与运用.在教育改革背景下，常规教学方法已经不再适用于高中数学课堂，多元智能理论提倡个性化教育，与教育改革思想相吻合，引起了教育领域的广泛关注与研究.为实现理想化的教育目标，笔者利用经验总结与案例分析等研究方法，在总结多元智能理论内核的基础上，提出教师可以通过设计个性化预习资源、巧妙创设教学情境、合理提供导学问题、补充多元化学习材料、实施分层评价等方式组织教学活动，营造良好学习氛围，实现多元智能理论与数学教育的紧密融合.

【关键词】多元智能理论；高中数学；教学策略

多元智能理论认为人的智能是由八种智能构成的，这八种智能的存在及其发展潜能，为人们提供了一种新的视角来认识人的内在素质与潜力，从而能够更好地帮助人们实现自我提升.随着教育改革的不断深化，教师不仅要关注学生在高中数学课堂中知识掌握情况，同时要关注学生内在素养的形成.因此，广大教师需要及时转变自身教育理念，解读多元智能理论的具体内涵，结合学科特色进行合理设计，保障学生能在充满智慧的数学课堂中取得收获，获得思维、能力的深层发展.

一、解读多元智能理论

为提高高中数学教学策略设计的有效性，教师需要明确多元智能理论的具体内涵，这样才能做到对症下药、有的放矢.在文章中，笔者利用文献调查法从现有的研究成果中吸取有利于本课题研究的相关内容，对多元智能理论的内涵进行总结：多元智能理论包含着的八种智能类型（言语语言智能、数理逻辑智能、音乐韵律智能、视觉空间智能、身体运动智能、交流交往智能、自我认识智能、自然观察智能）可以通过不同的方式进行评估和培养，人们在各种智能类型上的表现也不同多元智能理论强调了学习者的多元智能特点，强调学生在学习中有着特有的智能特点以及学习方式，教师要面向学生个体差异开展个性化教学.学者秋崇源在总结多元智能理论应用方法的同时，提出可以通过多样化的教学策略与活动激发学生内在学习动力与创新意识.刘群英也从多元化教学策略设计出发，强调满足学生不同智能类型的重要性.

二、基于多元智能理论的高中数学教学关注要点

教师基于多元智能理论组织高中数学教学期间，切忌沿用传统教学理念，应以素质教育为核心，关注不同智能学生成长需求，科学设计教学方案，尽量缩短班级内学生成绩差距.笔者对教学中需要关注的要点进行总结，以供广大教师参考借鉴：

多元智能理论强调学生学习的目的是促进个人的发展和自我实现，而不仅仅是为了应对考试.因此，在教学活动中教师需要及时更新自身教育理念，突破传统以分数定论的固态化思想，将重点放在培养学生综合能力上，促使学生成为课堂活动中的主体，帮助学生在自主構建、探索、创造的过程中发现知识、理解知识，养成良好的自主学习习惯，逐渐形成适应社会发展的必备品格与关键能力.

多元智能理论强调了学习者的个体化、情境化和主体化特点，在多元智能理论的指引下，教师要注意自身角色与学生角色之间的转变，充分关注学生在成长过程中的个性化差异以及诉求，对学生的学习能力、潜在智能、发展特点做出合理判断，以此作为教学策略设计的理论支持.这样，遵循学生最近发展区的教学策略充分贴合实际，使学生在多样化的学习机会与情境中实现各种智能的发展，确保每一名学生都能在课堂中得到进步与发展.

评价是教学活动中的关键环节，在多元智能理论下，教师在完成教学工作后需要针对学生在课堂中的表现做出及时评价，从学生的发展特点和多元智能特点等角度进行合理判断，为因材施教、多样化教学设计提供理论参考，这样能确保高中生数学教学实现可持续性发展.

学生在学习活动中的态度影响着他们的学习质量，目前许多学生对数学知识的探究热情不足、缺乏自主思考的内在动机.针对这一情况，教师要关注学生在学习生活中的表现，帮助学生及时调整学习思路，尝试建立数学课堂与生活实际的连接，使学生深刻地认识到数学在生活中的重要作用价值，从而提高学生对数学学习的重视程度，以更好地将多元智能理论融入课堂教学中.

三、基于多元智能理论的高中数学教学实践策略

（一）设计个性化预习资源，发展学生自学能力

高中阶段是学生学习习惯、思维能力养成的黄金时期，由于学生学习压力较大，难以在数学学习中做好充足的课前准备，从而导致课堂教学质量难以得到顺利发展.针对这一情况，在多元智能理论的支持下，教师可以根据班级内学生的智能特征，设计课前预习资源，指导学生有针对性地参与预习活动，借助此种方式在激发学生学习兴趣、培养学生自主学习习惯的同时，减轻教师在课堂中的教学压力，使教学活动更具效益.

教师根据学生不同智能设计预习内容，可以突破传统集中化预习的桎梏，避免因智能特征不同影响学生学习兴趣，保障预习工作的顺利进行，使得学生逐步掌握自主学习的方式与方法.

（二）巧妙创设教学情境，激活学生内在动力

在多元智能理论渗透过程中，教师发现大部分学生对真实的情境有着莫大的探索热情，对情境中包含的数学知识探究欲望明显.尽管个体具有的智能组合不同，但是其发展程度会受教育与环境的影响.因此，教师要充分发挥自身引导作用，尝试采用情境导入法，联系教学内容为学生设计形式多样且富趣味性的情境内容，充分体现并尊重学生的特点，为后续教学活动开展奠定基础.

以“集合的概念与表示”一课教学为例，通过本课学习学生应该掌握集合的定义以及基本概念，理解元素与集合之间的关系，并学会利用列举法以及描述法表示集合.根据目标要求，在教学活动开始前，为减轻学生的学习压力，提高学生对科学探究的积极性，教师可以借助信息技术手段分别向学生展示篮球、足球、正方体盒子、长方体文具盒、圆柱形薯片桶、魔方等生活中常见的事物图片，引导学生观察，并总结图片中事物的共同特点.在这一环节中，学生依靠真实情境通过观察的方式表示：图中提供的内容均是几何体.结合学生的反馈，教师再邀请大家将图中的几何体分为圆柱、球体、正方体这三类，然后再以此话题引出集合的概念，帮助学生构建数学模型，将图中的几何体视为研究对象“元素”，将元素组合的总体视为“集合”，如：圆柱就是薯片桶、奶粉罐、蜡烛等圆柱体的集合.这样，在真实情境中学生不仅能深化对集合的理解，还能感受到数学与生活的密切联系.

情境的导入充分考虑到不同学生的发展需求，能达到开发学生不同智能的目的.在后续环节中，教师还可以邀请学生对导入情境作出评价，切实掌握学生的个性化学习需求，以此提高导入的有效性，提高学生对数学学习的重视程度.

（三）合理提供导学问题，全面提高学生思维能力

在传统教学中，部分教师会直接向学生传授数学知识，指导学生通过大量练习达到巩固、理解的目的.此种模式与多元智能理论相悖，严重忽视了学生个人智能的发展趋势，无法顺利促进学生素养发展.对此，教师需要遵循多元智能理论的基本原则，尝试借助导学问题驱动学生思考，让学生在表达、思考的过程中发现言语语言及逻辑数理智能.

以“圆的方程”一课教学为例，在过往学习中学生借助平面直角坐标系建立了直线方程，并通过方程研究直线的性质与位置关系，在本课学习中大家需要了解圆的方程的建立以及圆的基本性质.为锻炼学生的言语语言智能，在教学活动开始前教师可以鼓励学生组建小组，并为其引出直线与方程知识，借助旧知识设计问题：1.在直角坐标系中确定直线的基本要素是什么？2.圆作为平面几何中的基本图形，确定它的要素是什么？什么叫圆？3.在平面直角坐标系中，任何一条直线都可以用一个二元一次方程表示，那么圆是否也可以用一个方程表示呢？如果能，这个方程又有什么特征呢？在问题的指引下，学生尝试由直线与方程之间的联系联想到圆的方程，积极回答教师的问题表达自己想法.根据学生的反馈，教师还可以围绕圆的定义、圆的标准方程等内容进行提问，营造良好的师生交互氛围，实现开发学生多元智能的目的.

在问题设计的过程中，教师不能盲目地单纯依靠教材提问，而是需要以宏观的角度分析不同学生的智能特征，设计有针对性且便于学生理解的问题，这样才能发挥提问的价值，帮学生在探索中发展思维.

（四）补充多元化学习材料，满足学生个性发展需求

教材中提供的学习内容无法满足部分学生发展的需求，在多元智能理论的指引下，教师可以基于原有教学资源，利用现代教育技术手段的优势为学生补充学习材料或练习资源，指导学生构建完善的知识结构，通过对数学知识的学习感受数学在生活中的重要作用，形成严谨、求真、务实的科学精神，达成理想化的教育目标.

以“抛物线”一课教学为例，在本课教学中教师借助平面直角坐标系，利用解几何研究问题的一般方法研究抛物线，帮助学生在课堂中掌握建立抛物线方程的方法，根据抛物线方程对抛物线的性质作出判断.根据学生在课堂中的智能特征以及学习表现情况，教师可以补充学习资料，拓展教学内容.例如，针对在课堂中学习表现中等的学生，教师可设计相关练习帮助学生巩固、深化所学内容，如：1.求经过点P（-2，-4）的抛物线的标准方程.2.已知抛物线的焦点为F（5，0），求抛物线的标准方程和准线方程.而针对学习能力较强、智能发展迅速的学生，教师可以在原有教学内容基础上，补充圆锥曲线的统一定义知识，邀请学生独立完成教材中提供的“双曲线时差定位法”训练，以此锻炼学生数学建模素养，促进学生多元智能发展.

在拓展资源期间，教师要根据学生能力进行设计，促使不同智能水平学生都能通过有效训练掌握运用基础知识与基本技能解决问题的方法，从而在多元化教学的支持下全面发展.

（五）实施分层评价，促进“教—学—评”一体化发展

将多元智能理论融入数学教学实践中，能实现提高学生核心素养的目的.新课标倡导“教—学—评”一致性，教师应发挥评价助教、导学的现实作用，形成灵活的应变与反应能力，以满足学生现实需求为目的设计评价标准，通过分层的方式实施个性化评价，鼓励大家根据评价标准及时调整自我，改善不良学习行为.

以“复数的几何意义”一课的教学为例，在本课教学中教师带领学生围绕“复数能否也用点来表示呢？”这一话题，对复数、复平面内的点和平面向量之间的关系进行梳理（如图1）：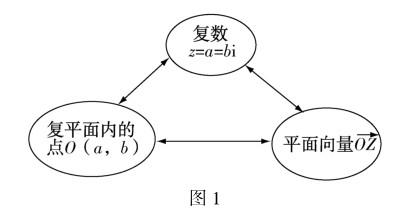

在完成基础教学任务后，教师针对学生在课堂中的表现作出评价.针对学习能力不强但能积极参与课堂活动的学生予以鼓励，从不同智能因素对学生学习方法进行总结，为学生设计科学的学习方案，保障其在評价的指引下提高多元智能.而针对学习能力较强且多元智能远胜于其他人的学生，教师在评价中需要对其进行适当提醒，指导此类学生多关注内省智能以及人际关系智能这两方面，使学生实现全面发展.

在多元智能理论视角下，教师要凸显评价对教学及学生学习的导向作用，破除传统以成绩为定论的评价思想，以个性化的评价方式保障教学质量.

结 语

综上所述，在教育改革背景下，教师应以多元智能理论为核心，遵循以生为本的教育理念设计教学活动，设法将学生的优势智能与弱势智能相结合，促使学生在更具开放性的课堂中积极参与、自主实践，逐步完善自我，以更好地适应未来社会发展需要.

【参考文献】

[1]吕升斗.基于信息化的高中数学智慧课堂教学研究[J].中国新通信，2022（21）：242-244.

[2]顾海燕.核心素养背景下的高中数学分层教学探讨[J].西部素质教育，2022（15）：85-87.

[3]拉毛才让.核心素养背景下的高中数学分层教学探讨[J].科学咨询（科技·管理），2020（10）：254.