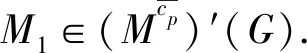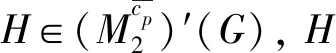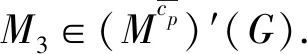二极大子群的G边界因子对群结构的影响
许 丽,陈心丹,缪 龙,2*,刘 威
(1.扬州大学数学科学学院,江苏 扬州 225002;2.河海大学理学院,南京 210098)
众所周知,极大子群和2-极大子群在群论研究中占有重要的地位,许多学者对其进行研究并取得大量成果[1-3].同时,利用子群的正规性研究群结构也是有限群理论的重要课题,如群G幂零当且仅当G的任意极大子群正规;若群G的任意2-极大子群正规,则G超可解等.随着研究的深入,不少学者通过对子群的正规性进行限制,给出了广义正规子群的概念.特别地,1996年,王燕鸣[4]提出c-正规子群的定义,并证明了群G可解当且仅当G的每个极大子群c-正规.随后,吕玉博等[5]在c-正规的基础上引入cp-正规子群的概念,从而给出了p-可解群的一些新刻画.此外,利用主因子来研究群结构也受到广泛关注,如若群G的每个主因子为素数阶的循环群,则G是超可解群.郭文彬等[6]通过限制主因子,给出了子群的G-边界因子定义;吴珍凤等[7]利用G-边界因子性质研究了p-可解群的结构.


1 预备知识
定义1[5]设H是群G的子群,p∈π(G).若G中存在一个包含HG的正规子群K,使得G=HK且H∩K/HG是p′-群,则H在群G中cp-正规.


定义4[6]设H是群G的真子群,则G的任意主因子K/HG称为H的G-边界因子.
定义5[11]设N是群G的正规子群.称G的子群H为N在G中的补充,如果G=NH.称补充子群H为N在G中的极小补充,如果对于H的任意真子群H1都有H1N 定义6[12]设N是群G的正规子群,M不是群G中的p-子群,但满足p∈π(M).称子群M为N在G中的极小p-补,如果满足MN=G并且对于M的任意极大子群M1都有M1N 引理2[5]设G是群,则G是p-可解当且仅当G的每个极大子群在G中cp-正规. 引理7[14]设G是群,p∈π(G).若对于任意P∈Sylp(G)都有NG(P)幂零,则G幂零. 引理8设G是群,若G∉S′p,则T′13(G)∩X′2(G)≠∅. 定理1群G∈S′p当且仅当任意H∈T′13(G),H的G-边界因子K/HG满足((K/HG)p)′=1. 证明 根据S′p的定义,必要性是显然的.下面证明充分性.假设结果不真且设G是极小阶反例.如果T′13(G)=∅,由引理8知G∈S′p,矛盾.设T′13(G)≠∅,显然G不是单群.若否,由K/HG=G/1和条件可知G∈S′p,矛盾. 综上所述,命题的充分性得证. 推论2群G∈S′p当且仅当对G的任意二极大子群H,H的G-边界因子K/HG满足((K/HG)p)′=1. 定理2群G∈S′p当且仅当任意H∈X′2(G),H的G-边界因子K/HG满足((K/HG)p)′=1. 证明 根据S′p的定义,只要考虑充分性.假设结果不真且设G是极小阶反例.若X′2(G)=∅,由引理8知G∈S′p,矛盾.若X′2(G)≠∅,不妨设G是单群,则HG=1且K/HG=G/1,从而对任意H∈X′2(G),有H的G-边界因子满足(Gp)′=1,进而G∈S′p,矛盾.下面讨论G不是单群的情况. 情形2(M3)G≠1.由引理6知M3=H2L 综上所述,命题的充分性得证. 定理3群G∈S′p当且仅当对任意H∈T′13(G)∩X′2(G),H的G-边界因子K/HG满足((K/HG)p)′=1. 证明 由S′p的定义,必要性是显然的.下面证明充分性.假设结论不成立并令G是极小阶反例.如果T′13(G)∩X′2(G)=∅,由引理8有G∈S′p,矛盾.因此,不妨设T′13(G)∩X′2(G)≠∅,则G不是单群.若否,由K/HG=G/1和条件知G∈S′p,矛盾. 情形2(M3)G≠1时,由引理6知M3=H2L 综上所述,命题的充分性得证.




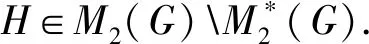
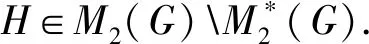



2 主要成果