求解四阶多项时间分数阶混合扩散波方程的二阶差分格式

高广花,徐 鹏

(南京邮电大学理学院,南京 210023)

近年来,在特征记忆、非局部性质[1-2]以及分形介质[3-4]等领域所遇到的复杂扩散行为均须利用分数阶导数或分数阶积分进行数学建模,使得分数阶微积分的理论和应用迅猛发展,而时间分数阶扩散方程和时间分数阶波动方程是两种极有价值的时间分数阶偏微分方程,其数值逼近已经被诸多学者研究[5-10]．然而,有些实际问题不能被时间分数阶扩散方程和时间分数阶波动方程单独描述,故一个同时包含分数阶扩散项和分数阶波动项的数学模型是一个很好的选项,通常称其为时间分数阶混合扩散-波方程．

作为单项时间分数阶偏微分方程的一种拓展,多项时间分数阶偏微分方程近年来备受关注．Gao等[11]对第二类Dirichlet边界下的空间四阶多项时间分数阶波方程建立了空间紧致差分格式,空间导数采用降阶法处理,时间Caputo分数阶导数应用L1公式近似;Zhao等[12]通过建立一种修正的L1公式对二维多项时间分数阶慢扩散方程进行离散,证明了数值格式在L2范数下的时间最优阶误差估计和空间最优收敛速率;Gao等[13]通过寻找多项分数阶导数线性组合插值逼近的一些特殊点,推导出至少能够达到二阶精度的数值微分公式,并将该公式应用于多项时间分数阶慢扩散方程的数值求解;Sun等[8]基于降阶法,通过选取时间方向超收敛点,推导并分析了求解多项时间分数阶波方程的两种时间二阶差分格式,并对其进行了稳定性和收敛性分析,分别证得空间方向上二阶和四阶收敛;Luchko[14]研究了有界域上广义多项时间分数阶扩散方程的初边值问题,用分离变量法和傅里叶方法证明了解的存在唯一性;Wei[15]提出求解一类多项时间分数阶扩散方程的全离散局部间断Galerkin方法,并通过严格的理论分析和有效的数值试验,证实了所得格式的稳定性与收敛性;Jiang等[16]采用分离变量法得到了不同边界条件下多项时间分数阶波方程和扩散方程的解析解．这些研究都是对多项时间分数阶扩散方程或多项时间分数阶波方程进行的,遗憾的是,求解时间分数阶扩散方程和时间分数阶波方程的数值方法不易直接推广到求解多项时间分数阶混合扩散-波方程．到目前为止,关于多项时间分数阶混合扩散-波方程数值逼近的文献较为有限．Sun等[17]对求解两项时间分数阶混合扩散-波方程的L1型差分格式提出了一种新的分析方法,证得了离散H1范数下的收敛性;Hao等[18]对多项时间分数阶混合扩散-波方程提出了一种基于L2逼近的隐式紧差分格式,并证明了该格式时间一阶和空间四阶收敛;Zhao等[19]通过空间方向上的线性三角有限元法和时间方向上的经典L1时步法离散,建立了求解二维多项时间分数阶混合扩散-波方程的全离散Crank-Nicolson型格式;Chen等[20]在空间方向应用Legendre谱方法,时间方向应用加权位移的Grünwald差分算子,对多项时间分数阶混合扩散-波方程进行离散化,提出一种时间方向二阶精度的数值格式;Feng等[21]利用L1公式对二维两项时间分数阶混合扩散-波方程的时间分数阶导数进行逼近,建立了差分求解格式,其时间方向精度不足二阶;Shen等[22]应用分离变量法和多元Mittag-Leffler函数的性质,研究了二维多项时间分数阶混合扩散-波方程的解析解,并基于L1公式建立了数值格式,对其收敛性和稳定性进行了严格分析;Liu等[23]考虑了二维多项时间分数阶混合扩散-波方程的初边值问题,在空间方向应用Legendre谱逼近,时间方向基于位移的Grünwald算子进行离散化,建立了一种隐式ADI谱格式,其时间方向二阶收敛．

上述工作都是对空间二阶多项时间分数阶混合扩散-波方程进行的研究,而很多实际问题仅有空间二阶导数是不能完全描述的,因此部分学者转而研究求解空间四阶时间分数阶偏微分方程．Nandal等[24]将时间分数阶导数基于L2-1σ公式逼近,在空间方向上构造紧线性算子,建立了求解一类非线性时滞变系数四阶分数阶慢扩散方程的线性紧差分格式,并利用能量分析法证得其无条件稳定且收敛,收敛阶达到时间二阶和空间四阶;Yao等[25]通过巧妙处理边界条件,建立了求解Neumann边界条件下空间四阶时间分数阶慢扩散方程的差分格式,其时间二阶、空间四阶收敛;He等[26]引入中间变量将原方程转变为低阶方程组,并对时间分数阶导数项和一阶导数项分别应用L1公式和二阶向后Euler公式离散,对空间方向应用有限元法,建立了求解一类非线性四阶时间分数阶微分方程的全离散格式,并证明了该格式的无条件稳定性和收敛性;Vong等[27]基于L1公式逼近时间分数阶导数建立了求解第一类Dirichlet边界条件下四阶时间分数阶慢扩散方程的空间紧致格式,其中临近边界两点处的局部误差为空间三阶,内点上为空间四阶;杨倩[28]对第一类Dirichlet边界值问题利用降阶法,在特殊点处考虑方程组后在方程两端同时作用紧算子,建立了全局四阶收敛的差分格式,而在第二类Dirichlet边界条件下,综合降阶法和L1公式,建立了求解时间分数阶混合扩散-波方程的差分格式,通过能量分析法证明了所得格式在离散最大模下的收敛性．到目前为止,对四阶多项时间分数阶混合扩散-波方程,尤其是空间多维问题和时间高精度格式的相关研究甚少．本文拟探讨数值求解如下四阶多项时间分数阶混合扩散-波方程初边值问题:

(1)

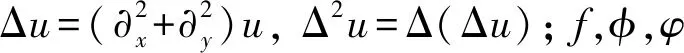
1 差分格式的建立

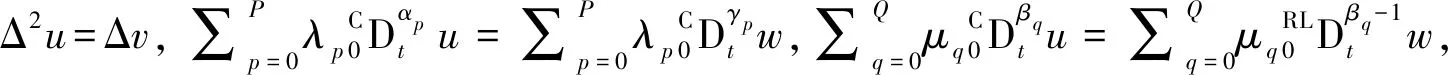
(2)

下面,建立求解等价问题(2)的有限差分格式．

1.1 预备知识

(3)

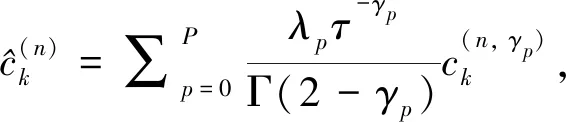
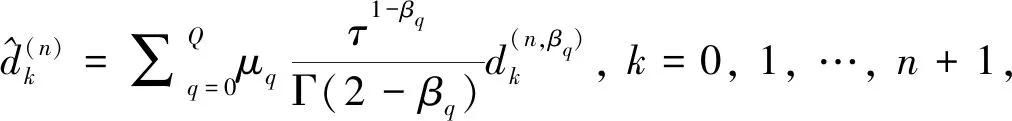
(4)

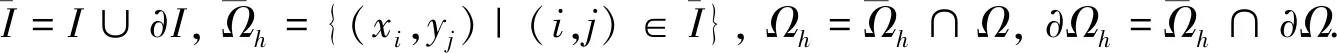
1.2 差分格式的建立

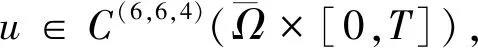
(5)

且存在正常数c1使得

(6)

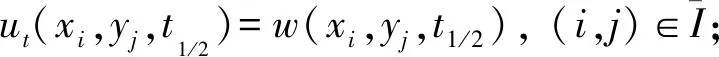
(7)

(8)

其中存在正常数c2使得

(9)

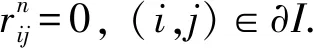
(10)

且存在正常数c3使得

(11)

根据初边值条件,有

(12)

(13)

(14)

(15)

(16)

(17)

(18)

1.3 差分格式的求解

设前n+1层的值{u0,w0,u1,w1,…,un,wn}已唯一确定,则由式(15)有

(19)

2 差分格式的分析

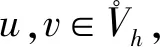
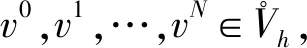
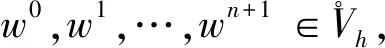
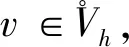
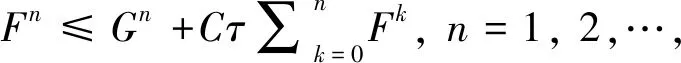
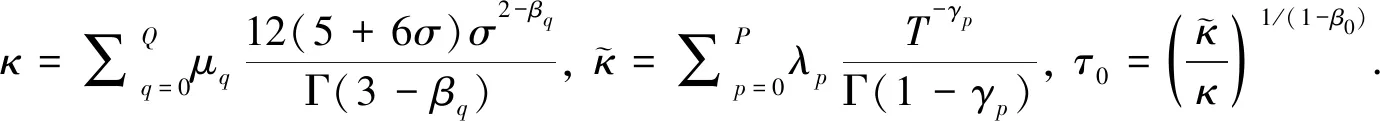
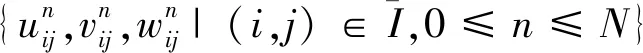
(20)

(21)

(22)

(23)

(24)

(25)

证明 i) ‖v1‖和‖w1‖的估计．当n=0时,由式(20)(n=0),(21),(23)～(25)知

(26)

(27)

(28)

(29)

(30)

将式(26)两边同时与w1做内积,得

(31)

2σ(δtΔhu1/2,v1)=σ(Δhw1,v1)+σ(Δhw0,v1)-2σ(Δhg0,v1)．

(32)

2σ(δtv1/2,v1)=2σ(δtΔhu1/2,v1)+2σ(δtp1/2,v1)．

(33)

将式(31)～(33)相加,由(Δhv1,w1)=(Δhw1,v1),得

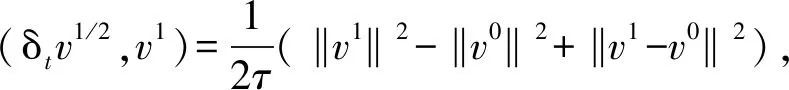
(34)

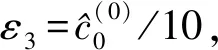
(35)

ii) ‖vn+1‖(n≥1)的估计．由式(20),(22)～(25)知

(36)

(37)

(38)

(39)

(40)

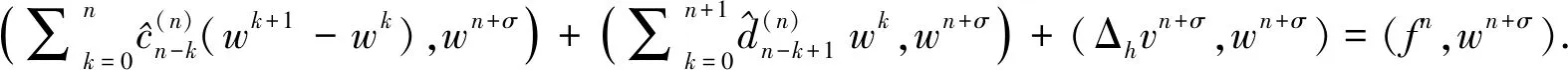
将式(37)两边同时与-vn+σ做内积,得

-(Δhwn+σ,vn+σ)=-(ΔtΔhun,vn+σ)-(Δhgn,vn+σ),1≤n≤N-1．

将式(38)两边同时与vn+σ做内积,得

(Δtvn,vn+σ)=(ΔtΔhun,vn+σ)+(Δtpn,vn+σ),1≤n≤N-1．

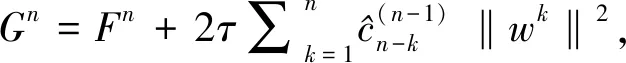
由上面分析可知,阶数在(0,1)和(1,2)区间内的时间分数阶导数同时出现,以及时空方向同时降阶是整个先验估计的难点所在．幸运的是,应用离散能量分析方法,结合文献[30]中的一些技巧,本文成功得到了理论分析结果．

由定理8,易得如下稳定性结果．

定理9差分格式(13)～(18)的解关于初值和源项是稳定的．

证明 将差分格式(13)～(18) 分别与式(5),(7)～(10)和(12)对应相减,可得如下误差方程组

注意到式(6),(9)和(11),应用定理8,可得存在正常数c7,使得

3 数值算例

数值计算通过编写MATLAB代码实现．

例1取L1=L2=π,T=1,P=Q=2．假设问题(1)有精确解u(x,y,t)=(t3+3t2+1)·sinxsiny,由此可确定相应的源项和初边值条件．

令h1=h2=h,F(h,τ)=max0≤n≤N‖Un-un‖∞．记Oτ=lb(F(h,2τ)/F(h,τ)),Oh=lb(F(2h,τ)/F(h,τ))．固定空间步长h=π/100时,取不同的参数值(λ0,λ1,λ2),(α0,α1,α2),(μ0,μ1,μ2) 和(β0,β1,β2),当时间步长从τ=1/10细化到1/160时,计算结果见表1．结果表明,时间方向数值收敛阶数与理论结果吻合较好．

表1 当h=π/100时最大范数误差和时间方向收敛阶Tab.1 Maximum norm errors and convergence orders in time with h=π/100

计算差分格式(13)～(18)的空间方向收敛阶时,固定时间步长τ=1/200,取不同的空间步长进行计算,其最大误差和数值收敛阶见表2．结果表明,该格式空间方向也达到理论上的二阶收敛．

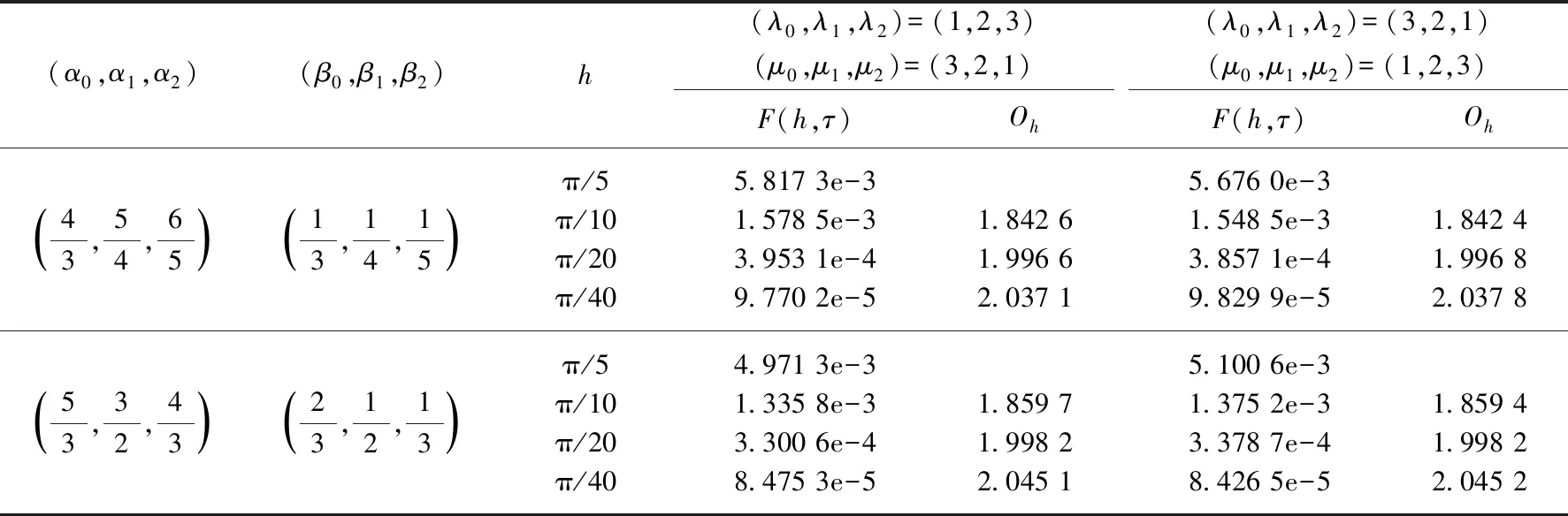
表2 当τ=1/200时最大范数误差和空间方向收敛阶Tab.2 Maximum norm errors and convergence orders in space with τ=1/200

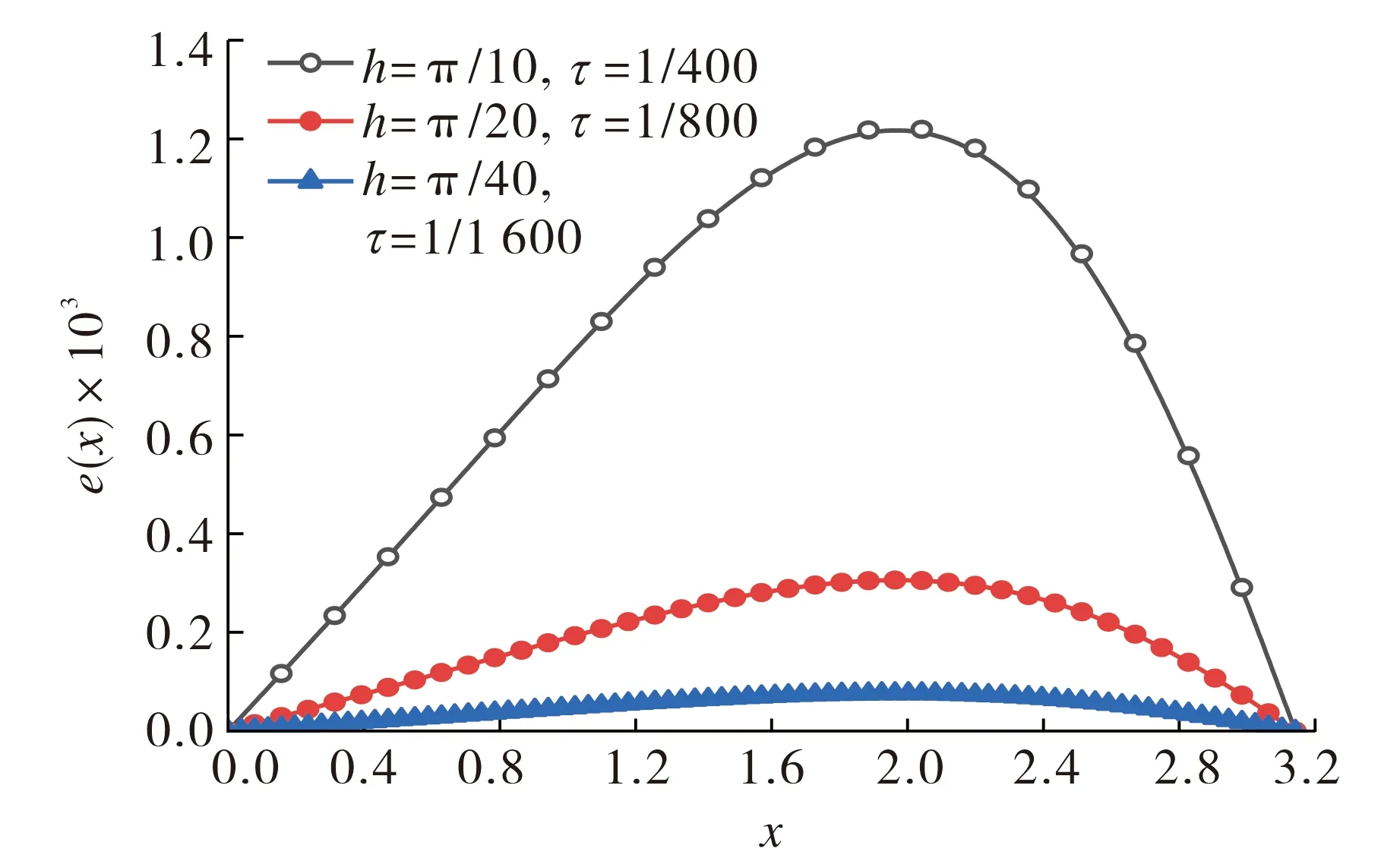
图1 t=1时不同步长下计算所得数值解误差曲线图Fig.1 The error curves of numerical solutions calculated under different step sizes at t=1

图1给出了t=1时不同步长下计算所得数值解的误差曲线图,其中e(x)=|U(x,π/2,1)-u(x,π/2,1)|．

4 结论

本文基于降阶法推导出了求解二维四阶多项时间分数阶混合扩散-波方程的一个新的差分格式．应用离散能量分析方法证得了格式的无条件稳定性和收敛性,并用数值算例进行了检验．值得一提的是,本研究中时空方向同时进行降阶处理,这使得理论分析具有一定的挑战．文中应用一些技巧,严格证明了差分格式的稳定性和收敛性．