带有未知干扰和混合时滞的非线性系统有限时间同步
路宗娅,于陆洋,崔 颖,刘玉荣*
(1.扬州大学数学科学学院,江苏 扬州 225002;2.阜阳师范大学数学与统计学院,安徽 阜阳 236037)
非线性系统的同步问题广泛出现在许多领域[1-3].近年来,大多数学者着重于研究非线性系统的渐近同步行为,即系统的状态在无限时间内实现同步[4-6].然而,在实际工程中系统通常被要求尽可能快地实现同步,甚至是在有限时间内同步.例如,在混沌保密通讯网络中,出于安全考虑,通常要求主-从网络同步,并要求解码信息在较短时间内被发送以避免解码信息的泄露;因此,Weiss等[7]首次提出有限时间稳定的概念,并探讨了一类非线性系统的有限时间稳定问题.目前,已有较多对非线性系统有限时间同步问题的研究.Mei等[8]基于有限时间稳定性理论,利用脉冲控制和周期间歇控制实现了2个具有非延迟和延迟耦合的非线性系统的有限时间同步,并给出有限时间同步的充分条件;Dong等[9]针对非严格反馈形式的非线性多智能体系统,探讨其有限时间一致容错控制跟踪问题.实际应用中,因复杂环境等因素的存在,不可避免地出现系统外部干扰以及信号传输时滞等现象.时滞和外部干扰将引起系统震荡,破坏系统的稳定性,从而导致系统难以实现有限时间同步,故考虑时滞和外部干扰对系统实现有限时间同步的影响尤为重要.Zhao等[10]通过探讨具有未知扰动的时滞混沌神经网络的滑模控制同步问题,设计了一个含积分结构和不连续控制律的滑动面,使得误差系统的轨迹在有限时间内收敛到该滑动面,且后续保持在该滑动面上;Li等[11]针对一类具有不确定扰动且节点不同的线性耦合动态复杂网络的有限时间同步问题,设计了一种新的控制器,避免了误差趋于零导致整体趋于无穷大的现象.本文拟研究一类具有混合时滞和未知干扰的非线性系统的有限时间同步问题,构造具有积分项的控制器,并导出系统实现有限时间同步的充分条件.
1 模型建立
考虑含N个节点且每个节点都是一个n维动力系统的耦合神经网络:
(1)
其中第i个节点的状态变量xi(t)=(xi1(t),…,xin(t))T;A,B,C为具有合适维数的常值矩阵;D=diag{d1,…,dn}和Dτ=diag{dτ1,…,dτn}分别表示节点i,j在t时刻和t-τ2(t)时刻的半正定内部耦合矩阵;f(xi(t))=(f1(xi1(t)),…,fn(xin(t)))T为神经元的激活函数;τ1(t),τ2(t)分别为时变内部时滞和耦合时滞;D1=(dij)n×n表示连接权重矩阵;σ(t)为分布时滞;外部耦合矩阵G=(Gij)N×N用于表示网络拓扑结构,若节点i与j之间有连接,则Gij>0,否则Gij=0,G是不可约的且满足耦合条件:
(2)
将系统(1)作为驱动系统,对应的响应系统为
(3)
其中yi(t)=(yi1(t),…,yin(t))T为响应系统中第i个节点的状态变量;ui(t)为控制输入;E为系统矩阵;Wi(t)=(Wi1(t),…,Win(t))T为未知干扰,满足‖Wi(t)‖2≤δ,δ为正常数.
对激活函数和时滞作如下假设:
(a) 激活函数fi(·)是连续有界的,fi(0)=0,且存在常数hi>0使得|fi(vi)-fi(wi)|≤hi|vi-wi|,其中vi,wi∈R;
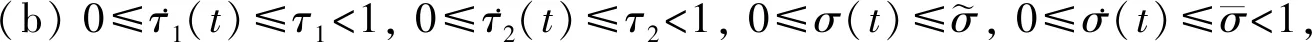
定义ei(t)=yi(t)-xi(t)为同步误差,则由系统(1)(3)可得
(4)
其中F(ei(t))=f(yi(t))-f(xi(t)),F(ei(t-τ1(t)))=f(yi(t-τ1(t)))-f(xi(t-τ1(t))).
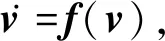


引理3[13]假设x,y∈Rn,则不等式2xTy≤ε-1xTM-1x+εyTMy成立,其中ε>0,M为具有合适维数的正定矩阵.

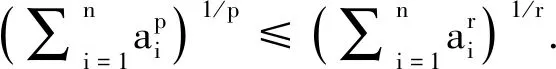

2 主要结果
定理1假设存在正数ε1,ε2,ε3,k以及对角矩阵G′=diag{G11,…,GNN},给定矩阵D=diag{d1,…,dn}和Dτ=diag{dτ1,…,dτn}满足:
(5)
(6)
(7)
(8)
其中H=diag{h1,h2,…,hn}>0,hi为假设(a)中的参数.
在假设条件(a)(b)下,设计控制器
(9)
其中sgn(ei(t))=(sgn(ei1(t)),sgn(ei2(t)),…,sgn(ein(t)))T,|ei(t)|α=(|ei1(t)|α,|ei2(t)|α,…,|ein(t)|α)T,常数μ>0,0<α<1,则系统(1)(3)在控制器ui作用下可实现有限时间同步.
证明 构造Lyapunov泛函
V(t)=V1(t)+V2(t)+V3(t)+V4(t),
(10)
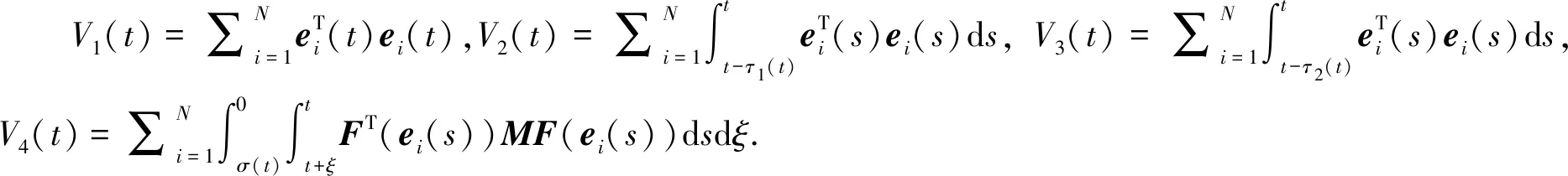
(11)
(12)
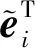
(13)
(14)
(15)
(16)
(17)
据引理3~4可得
(18)
据引理5~6可得
(19)
(20)

(21)
对V2(t),V3(t),V4(t)求导数,有
(22)
(23)
(24)
由式(21)~(24)可知
(25)
根据引理1知驱动系统(1)和响应系统(3)在控制器作用下达到有限时间同步.
3 数值仿真
笔者通过数值算例来验证理论结果的的正确性和有效性. 考虑系统(1)(3)的参数:
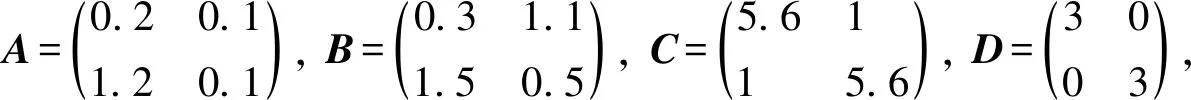
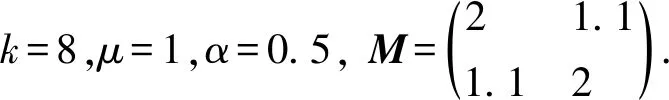
由定理1可知,在控制器(9)的作用下,驱动系统(1)和响应系统(3)的运动轨迹是有限时间同步的.
图1~2分别描述了驱动系统(1)和响应系统(3)的状态演化轨迹,图3给出了2个系统间的同步误差.

图1 xi(t) (i=1,2,3)的轨迹Fig.1 Trajectories of xi(t) (i=1,2,3)

图2 yi(t) (i=1,2,3)的轨迹Fig.2 Trajectories of yi(t) (i=1,2,3)
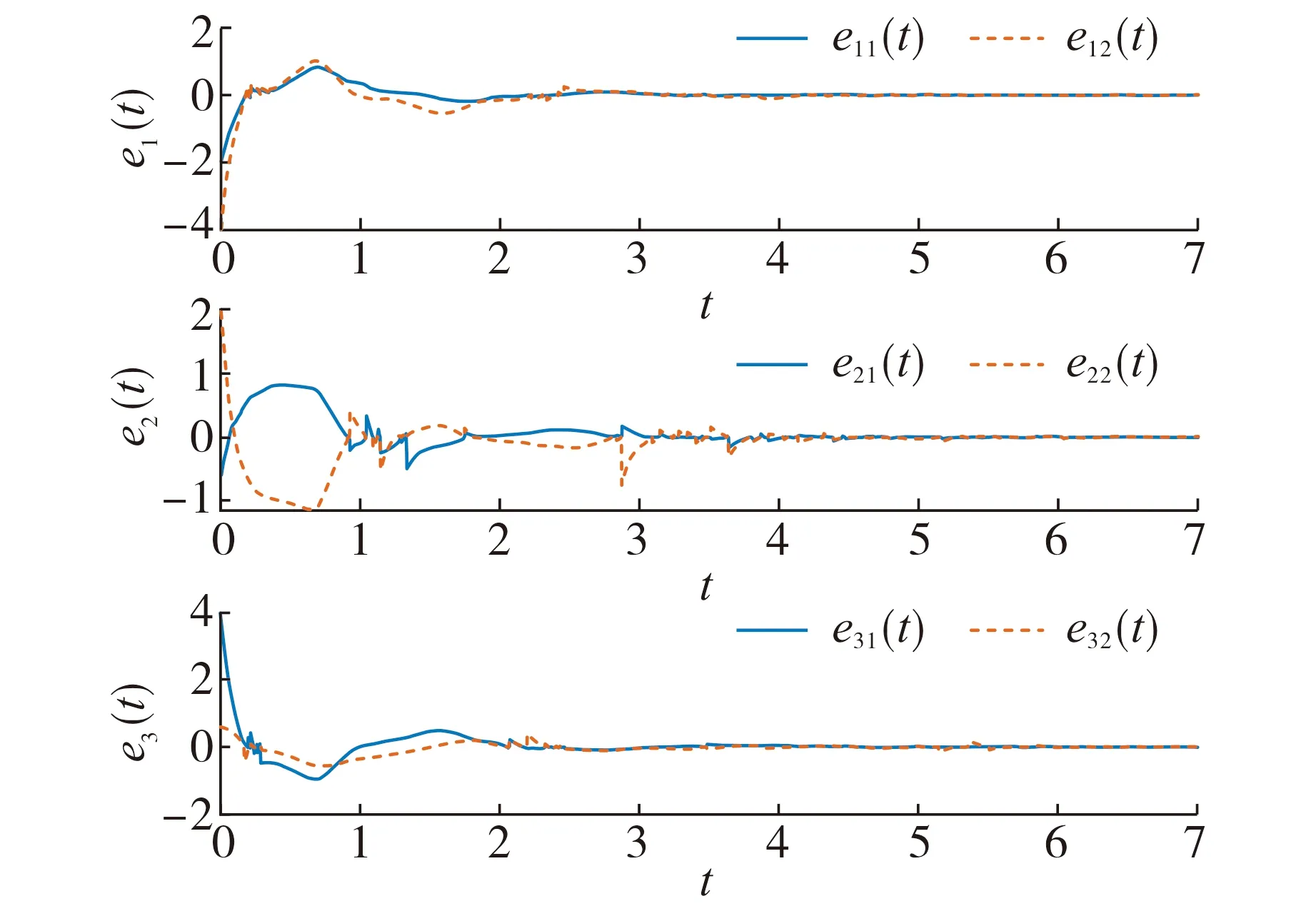
图3 驱动-响应系统的同步误差ei(t)(i=1,2,3)Fig.3 Synchronization errors ei(t)(i=1,2,3) of drive-response system

