共振条件下具有无界扰动方程的周期解

邢秀梅,王志国,黄强联

(1.伊犁师范大学应用数学研究所,新疆 伊宁 835000;2.苏州大学数学科学学院,江苏 苏州 215006;

3.扬州大学数学科学学院,江苏 扬州 225002)

x″+n2x+f(x)+g(x′)=p(t)

(1)

2π周期解的存在性．与Ma[10]研究的方程相比,方程(1)增加了阻尼项g(x′),在一定条件下也可得到方程(1)存在2π周期解．

1 预备知识

方程(1)等价于平面系统

x′=y,y′=-n2x2-f(x)-g(y)+p(t)．

(2)

引理1设条件(ii)和(iii)成立,则方程(2)满足(x(t0),y(t0))=(x0,y0)的解(x(t),y(t))存在于整个t轴．

证明 由条件(ii)知,存在M0>0,当|x|≥M0时,|F(x)|≤4-1n2x2．令K(t)=2-1y2(t)+2-1x2(t)+F(x(t))+M+1,其中M=max|x|≤M0|F(x)|．由式(1)直接计算,得|K′(t)|≤(D+P)K(t),其中P=maxt∈R|p(t)|．两端积分,有

K(t0)e-(D+P)|t-t0|≤K(t)≤K(t0)e(D+P)|t-t0|,

(3)

故2-1y2(t)+2-1n2x2(t)≤K(t0)e(D+P)|t-t0|．再由解的延拓定理知,解(x(t),y(t))存在于整个t轴．证毕．

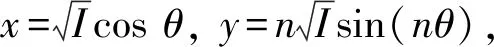
(4)

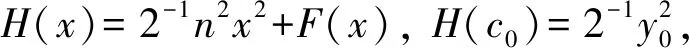
引理2设条件(ii)～(iv)成立,则当c0充分大时,有θ′(t)<0,t∈[t0,t0+4π]．

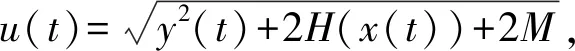
(5)

(6)

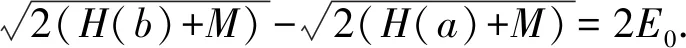
c0-a<ζ,b-c0<ζ．

(7)

n2a2+2F(a)≤n2I2+2F(x(t))≤n2b2+2F(b)．

记解Λ绕原点顺时针转一圈所用时间为τ(θ0,I0),则下述结论成立．

引理4若条件(i)～(iv)成立,则对充分大的c0,有τ(θ0,I0)=2πn-1+o(1),且τ(θ0,I0)<2πn-1．

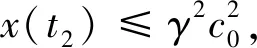
注与文献[1]相比,本文在证明定理的过程中估计τ(r0,θ0)的下限并未对Poincaré 映射,而通过对后继映射应用不动点定理得到2π周期解的存在性,简化了估计的难度．

2 主要结论

定理5设条件(i)～(iv)成立,则方程(1)至少存在一个2π周期解．