广义星形函数子族的对数逆系数
2022-12-09 01:12王雅倩熊良鹏
扬州大学学报(自然科学版) 2022年4期
王雅倩,熊良鹏
(江西科技师范大学数学与计算机科学学院,南昌 330038)
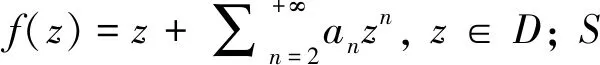
(1)
Ponnusamy等[4]在研究S各类子族Γn(F)的最优界时发现,在很多情况下得到对数逆系数的界并不容易.尽管解决S各类子族的系数估计问题已吸引了众多研究者的关注[5-6],但是在一些情况下,对数逆系数的精确估计依然存在太多问题和困难.本文拟探讨Sα,β(A,B)的全部对数逆系数的精确边界,以期丰富已有成果.
1 预备知识


根据定义1,通过调整不同的参数可得到很多重要的解析子类[7-11].
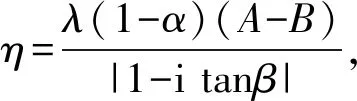
(2)

2 主要结果
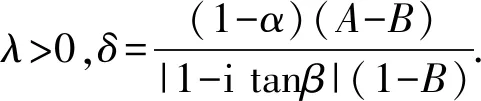
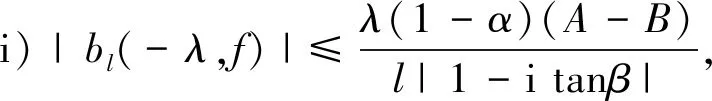
ii) 设λ>1,L1={1,2,…,[λ]-k},L2={1,2,…,[λ]-k+1},L3={[λ]-k+1,[λ]-k+2,…},L4={[λ]-k+2,[λ]-k+3,…}.另记Ni={λδ∉N+,l∈Li},i=1,3和Nj={λδ∈N+,l∈Lj},j=2,4则有
其中δ∈Ik(λ),k=0,1,…,[λ]-1.特别地,当δ∈I[λ]-1(λ),有
(3)


(4)
因(η+nB)2-n2=[η+n(1+B)][η-n(1-B)]=(1-B)[η+n(1+B)](λδ-n).显然,式(4)右边累加求和的符号完全由λδ-n决定,下面对此展开讨论.
1) 若0<λ≤1,则λδ-n≤0,n=1,2,…,l-1,故由式(4)得l2|bl(-λ,f)|2≤η2.定理1(i) 得证.
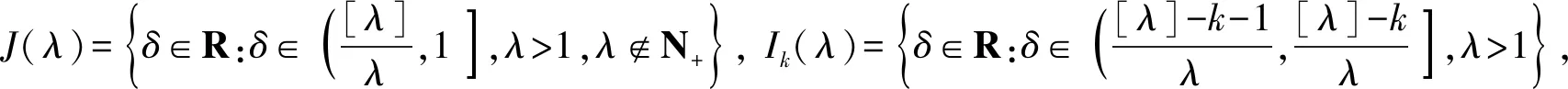
(5)
(6)

(7)
同理,对式(6)采用数学归纳法,可得
(8)
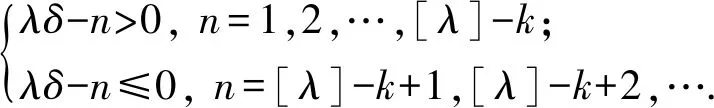
|b1(-λ,f)|≤η,|bl(-λ,f)|≤η/l,l=2,3,…,
故完成了式(3)的证明.

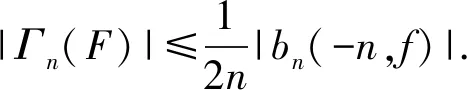
猜你喜欢
语数外学习·高中版中旬(2021年12期)2021-03-09
语数外学习·高中版上旬(2020年8期)2020-09-10
娃娃乐园·3-7岁综合智能(2017年9期)2018-02-01
娃娃乐园·3-7岁综合智能(2017年8期)2018-02-01
娃娃乐园·3-7岁综合智能(2017年7期)2018-02-01
速读·中旬(2017年8期)2017-09-04
新高考·高一数学(2016年10期)2017-07-06
新民周刊(2016年15期)2016-04-19
新民周刊(2016年15期)2016-04-19
中学生数理化·高二版(2008年7期)2008-06-15

