对称群Sn中元素的分解

陈 杏,史彦青,李立斌

(扬州大学数学科学学院,江苏 扬州 225002)

因为任一有限群均同构于某一对称群的子群[1],故对称群是代数中的重要研究对象之一,也是其他数学分支特别是组合数学重要的工具之一．Xu[2]证明了当且仅当n≥5时对称群Sn的Cayley图之间存在NNN-图;Libman等[3]计算了对称群的共轭直径;Morotti[4]刻画了特征2中对称群的不可约张量积;Giannelli等[5]刻画了对称群的Sylow子群的线性特征;王绍恒等[6]采用理论分析与编程判断相结合的方法,获得了Sn的全部极大子群的生成元及子群的阶等结果;Tsang[7]刻画了GaloisSn扩张上Hopf-Galois结构;Miller[8]刻画了对称群的奇偶性和其他若干性质;何立官等[9]证明了对称群Sn可由其阶|Sn|与最高元素的阶唯一刻画;Pan[10]证明了关于对称群中元素乘积阶的一个猜想;Kleshchev等[11]给出了有限对称群的不可约模表示维数的下界．本文拟讨论对称群Sn(n≥4)中元素的分解性质．

1 预备知识

假设n是正整数,令A={1,2,…,n},Sn是A上的对称群．为了方便,文中用(a1a2…am)表示长为m的循环置换,其中a1,a2,…,am∈A;对任意σ∈Sn,用ο(σ)表示σ的阶．

引理1[1]设σ∈Sn,则σ可以写成若干个互不相连的循环置换的乘积．

引理2[1]i) 循环置换(a1a2…am)的阶是m;ii) 若干个互不相连的循环置换的乘积与次序无关．

引理3[1]设σ∈Sn．若σ=σ1σ2…σt,其中σ1,σ2,…,σt是长为r1,r2,…,rt的互不相连的循环置换,则σ的阶是r1,r2,…,rt的最小公倍数．

引理4[1]设σ∈Sn,则σ可以表示成若干个对换的乘积,且奇偶性由σ唯一确定．

引理5[1]长为奇数的循环置换是偶置换,长为偶数的循环置换是奇置换．

本文中出现的其他术语出自文献[1,12]．

2 主要结果

引理6设n≥4,则Sn中任意长度为m的循环置换可表示成2个二阶元的乘积．

证明 任取σ=(a1a2…am)∈Sn是长为m的循环置换,若m=1,则结论显然成立．若m=2,即σ=(a1a2),注意到n≥4,则可取a3,a4∈A,且{a1,a2}∩{a3,a4}=∅．令τ=(a3a4),δ=(a1a2)·(a3a4),则τδ=(a1a2)=σ,且ο(τ)=ο(δ)=2,故结论成立．

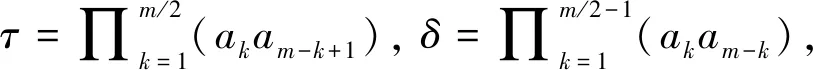
定理7设n≥4,则∀σ∈Sn,σ均可写成2个二阶元的乘积．

证明 任取σ∈Sn,由引理1可知,σ可以表示成互不相连的循环置换的乘积,不妨设σ=(a11a12…a1r1)(a21a22…a2r2)…(as1as2…asrs)．由引理6,得(ai1ai2…airi)=τiδi,其中τi,δi是不相连的二阶元的乘积,则ο(τi)=ο(δi)=2,i=1,2,…,s．注意到τi与δi(i≠j)互不相交,有σ=(τ1δ1)(τ2δ2)…(τsδs)=(τ1τ2…τs)(δ1δ2…δs)．令τ=τ1τ2…τs,δ=δ1δ2…δs,则τ,δ为互不相连的二阶元的乘积,于是ο(τ)=ο(δ)=2,且τδ=σ．结论成立．

引理8设n≥4,则Sn中任意长度为m的循环置换都可以表示成一个二阶元和一个三阶元的乘积,其中m>1．

证明 任取σ=(a1a2…am)∈Sn是长为m的循环置换．如果m=2,即σ=(a1a2),注意到n≥4,可取a3∈A,且{a1,a2}∩{a3}=∅．令τ=(a2a3),δ=(a1a3a2),则τδ=(a1a2)=σ,且ο(τ)=2,ο(δ)=3,故结论成立．如果m=3,即σ=(a1a2a3),注意到n≥4,取a4∈A,且{a1,a2,a3}∩{a4}=∅．令τ=(a1a4)(a2a3),δ=(a1a3a4),则τδ=(a1a2a3)=σ,且ο(τ)=2,ο(δ)=3,故结论成立．如果3

命题9设n≥4,则∀σ∈Sn,且ο(σ)=3,σ均可写成一个二阶元和一个三阶元的乘积．

证明 任取σ∈Sn,且ο(σ)=3,由引理1可知,σ可以表示成互不相连的三阶循环置换的乘积．① 当σ是1个三阶循环置换时,由引理8可知,结论成立．② 当σ是2个三阶循环置换的乘积时,不妨设σ=(a1a2a3)(a4a5a6)．令τ=(a1a5)(a2a6),δ=(a1a6a4)(a2a3a5),则τδ=(a1a2a3)(a4a5a6)=σ,且ο(τ)=2,ο(δ)=3,故结论成立．③ 当σ是r(r>2)个三阶循环置换的乘积时,不妨设σ=σ1σ2…σr,其中ο(σi)=3,i=1,2,…,r．由②可知,∃τ1,δ1∈Sn且ο(τ1)=2,ο(δ1)=3,使得τ1δ1=σ1σ2,有σ=σ1σ2…σr=τ1δ1σ3σ4…σr．注意到δ1与σi(i=3,…,r)不相交,令τ=τ1,δ=δ1σ3σ4…σr,则τ为2个互不相连的二阶循环置换的乘积,δ为r个互不相连的三阶循环置换的乘积,故ο(τ)=2,ο(δ)=3,且τδ=σ．结论成立．

定理10设n≥4,则∀σ∈Sn,且ο(σ)>2,σ均可写成一个二阶元和一个三阶元的乘积．

证明 任取σ∈Sn,由引理1知,可将σ表示成互不相连的循环置换的乘积,σ=σ1σ2…σr．由ο(σ)>2知,{ο(σi)|i=1,2,…,r}≠{2}．若{ο(σi)|i=1,2,…,r}={2,3},则结论显然成立．若{ο(σi)|i=1,2,…,r}={3},则ο(σ)=3,从而由命题9知,结论成立．若∃i∈{i=1,2,…,r},使得ο(σi)>3．不妨设σ=σ1σ2…σsσs+1…σtσt+1…σr,其中ο(σi)=2,ο(σj)=3,ο(σk)>3,i=1,2,…,s;j=s+1,s+2,…,t;k=t+1,t+2,…,r．由引理8知,当k≥t+1时,σk=τkδk,其中τk是互不相连的二阶循环置换的乘积,δk是互不相连的三阶循环置换的乘积．注意到σl,τi与δj(i≠j)互不相交,l=1,2,…,t,于是σ=(σ1σ2…σs)(σs+1…σt)(τ1δ1)(τ2δ2)…(τsδs)=(σ1σ2…σsτ1τ2…τs)(σs+1…σtδ1δ2…δs)．令τ=σ1σ2…σsτ1τ2…τs,δ=σs+1…σtδ1δ2…δs,则τ为互不相连的二阶循环置换的乘积,δ为互不相连的三阶循环置换的乘积,故ο(τ)=2,ο(δ)=3,且τδ=σ．结论成立．

注当ο(σ)=2时,结论不一定成立．例如:在S4中,(12)(34)不能写成一个二阶元和一个三阶元的乘积．事实上,假设(12)(34)=τδ,其中ο(τ)=2,ο(δ)=3．因为δ∈S4,所以δ是一个三阶循环置换,由引理5知,δ和τδ是偶置换,于是由引理4知,τ是偶置换．因为ο(τ)=2,所以τ是2个不相交的对换的乘积．由S4中置换的乘积可知,ο(τδ)=3,与假设矛盾．而在S5中,(12)(34)可以写成一个二阶元和一个三阶元的乘积,只须令τ=(12)(45),δ=(354),则τδ=(12)(45)(354)=(12)(34)．