关于ss-拟正规子群和c-正规子群

程 丹, 徐颖吾

(西安工程大学 理学院, 陕西 西安 710048)

1 预备知识

首先介绍与ss-拟正规子群有关的结果:

引理1[2]设H是G的ss-拟正规子群,K≤G且N是G的正规子群.

1) 如果H≤K, 那么H是K的ss-拟正规子群.

2)HN/N是G/N的ss-拟正规子群.

3) 如果N≤K且K/N是G/N的ss-拟正规子群, 那么K是G的ss-拟正规子群.

4) 如果K是G的拟正规子群, 那么HK是G的ss-拟正规子群.

与c-正规子群相关的引理如下:

1) 如果X在G中c-正规, 那么X在H中c-正规.

2) 设π是素数集,N是G的正规π-子群,X是G的π′-子群. 如果X在G中c-正规, 那么XN/N在G/N中c-正规.

3) 设N是G的可解极小正规子群,N有一个在G中c-正规的极大子群, 那么N是素数阶的循环群.

4) 假设p∈π(G)使得(|G|,p-1)=1. 如果Gp拥有一个极大子群H且H是G的c-正规子群, 那么G的p-幂零剩余G(P)是一个p-群.

引理4[11]设G是一个群且p是一个素数, (|G|,p-1)=1.

1) 如果N是G的正规子群, 那么N≤Z(G).

2) 如果G有一个循环p-子群, 那么G是p-幂零的.

引理5[1]设N是G的正规Hall子群, 则

1)N在G中有补;

2) 若N或G/N可解,H和H1是N在G中的2个补群, 则存在u∈N使得Hu=H1.

2 主要结果

定理设G是有限群,p∈π(G)且满足(|G|,p-1)=1. 假设P是G的一个Sylowp-子群, 如果M(P)的每个元素在G中或是ss-拟正规的或是c-正规的, 那么G是p-幂零的.

证明假定结论不真, 我们设G是极小反例.

置M(P)={P1,P2,···,Pm}. 由假设, 每个Pi要么在G中ss-拟正规要么在G中c-正规. 不失一般性, 设存在一个自然数k(1≤k≤m), 使P1，···，Pk在G中c-正规, 而Pk+1，···，Pm在G中ss-拟正规.

由于Pi(i=1,···,k)在G中c-正规, 由引理2之4)知,G/(Pi)G是p-幂零的.

记

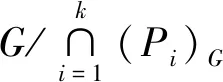
所以N≠1.

我们分4个步骤来证明.

第1步 证明G有Hallp′-子群H.

因为商群G/N是p-幂零的, 所以商群G/N存在正规Hallp′-子群M/N. 那么M有正规Hallp-子群N. 由引理5,M有p-补, 记为H. 这个H即为G的Hallp′-子群. 即为所求.

第3步 记N*=N∩Wj. 考察

N∩Wj=P∩N∩Wj=N∩(P∩Wj)=N∩(P∩PjH)=N∩Pj

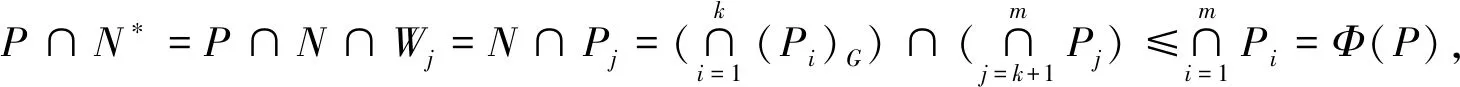
又由于G/Φ(P)是p-幂零的且p-幂零群类是一个饱和群系, 我们得出G是p-幂零的. 得出最后的矛盾.

证毕.

推论假设G是一个群. 如果M(G)的每个元素在G中要么是ss-拟正规要么是c-正规, 那么G有超可解型Sylow塔.

证明设p是|G|的最小素因子,P是G的Sylowp-子群. 由假设M(P)的每个元素或是c-正规或是ss-拟正规, 由上一定理可知,G满足该定理条件, 从而G是p-幂零的. 设U是G的正规p-补, 由引理1(2)和引理2(2)有,U满足推论的条件, 由极小反例法可知,U拥有超可解型Sylow塔, 形如,U▷U1▷U2▷…▷Ur, 从而G就有超可解型Sylow塔, 形如,G▷U▷U1▷U2▷…▷Ur.证毕.