全直线上四阶方程的Laguerre-Laguerre复合谱逼近
蔡耀雄, 庄清渠
(华侨大学 数学科学学院, 福建 泉州362021)
近三十年来,关于求解四阶微分方程的谱方法的研究有很大进展.Shen[1]采用Legendre-Galerkin谱方法求解二阶和四阶微分方程;Kwan等[2]考虑可分离椭圆型问题的并行谱元计算;Shen等[3]采用Legendre Petrov-Galerkin逼近法数值求解四阶方程;文献[4-5]分别研究一维和二维四阶方程的谱元计算;庄清渠等[6]研究四阶常微分方程的Birkhoff配点法;文献[7-8]分别研究两类四阶积分微分方程的谱逼近;Chen[9]研究四阶Cahn-Hilliard方程的Legendre-Galerkin谱逼近.上述文献研究的是有界区域上的四阶方程,对于无界区域上的四阶方程也有一些研究工作.叶小华[10]研究一维半直线区域四阶方程的Legendre-Laguerre复合谱方法;Zhuang等[11]研究一维半无界区域四阶方程的Legendre-Laguerre耦合谱元计算;李敏等[12]研究半无界条状区域四阶方程的Laguerre-Legendre混合谱逼近;李珊等[13]研究半直线区域上四阶椭圆型方程的有理Legendre函数全对角化谱方法;Yu等[14]研究全直线区域上的对角化Legendre有理谱方法.本文用Laguerre-Laguerre复合谱方法求解全直线上的四阶方程,并与一类Hermite谱方法进行对比,主要考虑方程的数值计算.
1 问题及复合逼近形式
记I:=(-∞,∞),考虑如下的四阶问题,即
(1)

d(u,v)=(f,v), ∀v∈V,
(2)
式(2)中:d(u,v):=λ2(u,v)+λ1(ux,vx)+(uxx,vxx),∀u,v∈V.
对问题(2),用Laguerre-Laguerre复合谱方法进行求解.首先,将(-∞,∞)剖分成I1=(-∞,0),I2=(0,∞)两部分.然后,在两个区间上分别采用Laguerre谱方法进行逼近.
记uI1:=u|I1,uI2:=u|I2,N=(N1,N2) ,令PN(Ω) 为Ω上次数不超过N的全体多项式组成的空间,并记
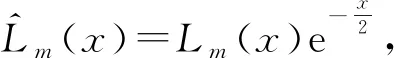
(3)
(4)
则问题(1)的Laguerre-Laguerre复合逼近形式如下:找uN∈VN,使得
d(uN,vN)=(f,vN), ∀vN∈VN.
(5)
2 计算实施
Laguerre多项式Lm的基本性质[15]如下,即
(6)
(7)
令
(8)
(9)


(10)
(11)

类似于文献[11,16]求解高阶方程的过程,Laguerre-Laguerre复合逼近问题(5)所对应的线性系统可通过如下3个步骤进行求解.

(12)

(13)
(14)
3) 结合.由式(13),(14)可知,对任意的vN∈VN,有
(15)
因此,问题(5)的解为
(16)
问题(5)分解成了两个相对独立的子问题,子问题(12)和(13)分别由九对角问题和五对角问题组成,因而容易进行求解.

(λ2C+λ1B+A)U2=F2.
(17)
由Laguerre函数的正交性可得
由此可知,矩阵都是对称的,且最多是五对角阵,因而式(17)可以有效地求解.子问题(13)在I1上的代数方程组与其在I2上的代数方程组类似.
子问题(12)对应的代数方程组的系数矩阵与子问题(13)相同.子问题(12)对应的代数方程组的右端项可通过对φ1(x),φ2(x)进行求导,有
又因为
从而在区间I1上,有
以及
而在区间I2上,有
以及
因此,可得子问题(12)对应代数方程组的右端项.
对于子问题(14),由于


图1 最大误差随的变化情况Fig.1 Maximum errors change with
3 数值算例
算例1在问题(1)中,固定λ1=λ2=1,取精确解为
u(x)=sin(x)e-σx2.

其次,当σ=0.01和σ=0.02时,分别利用Laguerre-Laguerre复合谱方法及Hermite谱方法进行计算,得到的最大误差,如表1所示.由表1可知:当σ比较小时,用Laguerre-Laguerre复合谱方法进行逼近的误差比用Hermite谱方法进行逼近的误差要小得多.因此,Laguerre-Laguerre复合谱方法逼近更具优越性.

表1 两种方法在u(x)=sin(x)e-σx2时的最大误差Tab.1 Maximum errors by two ways for u(x)=sin(x)e-σx2


表2 两种方法在时的最大误差Tab.2 Maximum errors by two ways for
4 结束语
将全直线区域剖分为两部分,进而构造了求解全直线上四阶方程的Laguerre-Laguerre复合谱方法.数值结果表明,复合方法具有谱收敛性.同时,通过与纯Hermite谱方法的比较可以看出,复合谱方法对求解具有衰减缓慢解析解的问题具有优越性.

