内配螺旋箍筋方钢管超高强混凝土柱的偏压受力性能
黄经纬, 许力, 胡红松,2, 张鹏程
(1. 华侨大学 土木工程学院, 福建 厦门 361021;2. 华侨大学 福建省结构工程与防灾重点实验室, 福建 厦门 361021; 3. 厦门大学 建筑与土木工程学院, 福建 厦门 361005)
因结构性能良好和施工方便等优点,钢管混凝土(CFST)柱已被广泛地应用于高层建筑.在超高层建筑中,框架柱承受非常大的荷载作用,为了满足承载力的要求,框架柱的截面尺寸往往较大.采用超高强混凝土可有效降低框架柱的截面尺寸,但也会降低框架柱的延性.此外,在相同含钢率的条件下,方钢管混凝土柱中的混凝土受约束程度不如圆钢管混凝土柱[1],导致方钢管混凝土柱的延性降低更为明显.为确保采用超高强混凝土的方钢管混凝土柱具有足够的延性,可以在方钢管混凝土柱的内部设置圆钢管[2-4]、螺旋箍筋[5-7]或纤维增强复合材料(FRP)管[8-9],从而给内填混凝土施加额外约束.
螺旋箍筋在实际工程中应用广泛,可有效提高方钢管混凝土柱的变形能力,但对内配螺旋箍筋方钢管混凝土(SCCFST)柱的研究还相对较少.Ding等[10]对6个不同体积配箍率的SCCFST柱试件开展轴压试验.Teng等[5]对4个内配高强螺旋箍筋的方钢管混凝土柱试件进行轴压试验.陈宗平等[11]完成20个SCCFST柱试件的轴压试验,变化参数为螺旋箍筋间距、箍筋直径、混凝土强度和钢管的宽厚比.在上述试验中,除了Teng等[5]采用的混凝土抗压强度为80 MPa,其余试验采用的混凝土抗压强度均低于50 MPa.此外,高层建筑中的框架柱承受轴力和弯矩的共同作用,而现有试验只研究了SCCFST柱的轴压性能.因此,有必要对这种新型组合柱的偏压性能进行研究.基于此,本文对内填混凝土抗压强度为111 MPa的SCCFST柱开展偏压试验,研究SCCFST柱的破坏过程、承载力、延性和控制截面的荷载-变形响应.
1 试验方案
1.1 试件设计
设计普通方钢管混凝土柱(编号为EC-O-0.32)、内配普通螺旋箍筋方钢管混凝土柱(编号为EC-N-0.32)和内配高强螺旋箍筋方钢管混凝土柱(编号为EC-H-0.32)3种类型的试件.配箍试件构造,如图1所示.普通方钢管混凝土柱除了未配置螺旋箍筋外,其余构造与配箍试件相同.试件钢管由4块厚度(t)为5.5 mm的钢板用坡口焊焊接而成,钢管截面宽度(B)为200 mm,宽厚比(B/t)为36.4,试件高度(L)为600 mm.为防止试件端部因应力集中而过早破坏,采用围焊钢板的方法,对钢管两端100 mm的范围进行加强.两端加强区内的螺旋箍筋也进行加密处理,箍筋的间距为中间段的一半.钢管的两端各焊一块厚度为30 mm的端板,试验时,端板与刀铰通过螺栓连接.

(a) A-A截面 (b) B-B截面 图1 配箍试件构造(单位:mm)Fig.1 Construction of specimens with spiral stirrup (unit: mm)
试件的主要参数,如表1所示.表1中:D为箍筋约束区混凝土直径(测量至螺旋箍筋外径);Acc为箍筋约束区混凝土横截面积;Ac为内填混凝土总截面积;dsp为螺旋箍筋的直径;Asp为螺旋箍筋的横截面积;s为中间段箍筋间距;fyp为螺旋箍筋的屈服强度;e为轴力偏心距;e/B为偏心率;ρs为螺旋箍筋体积配箍率,定义为
(1)

表1 试件的主要参数Tab.1 Main parameters of specimens
1.2 材性性能
厚度为5.5 mm的钢板、螺旋箍筋直径为8.0 mm的普通钢筋和高强钢筋的实测应力-应变(σ-ε)曲线,如图2所示.因高强钢筋的σ-ε曲线无屈服平台,将其0.2%残余应变对应的应力值取为屈服强度.
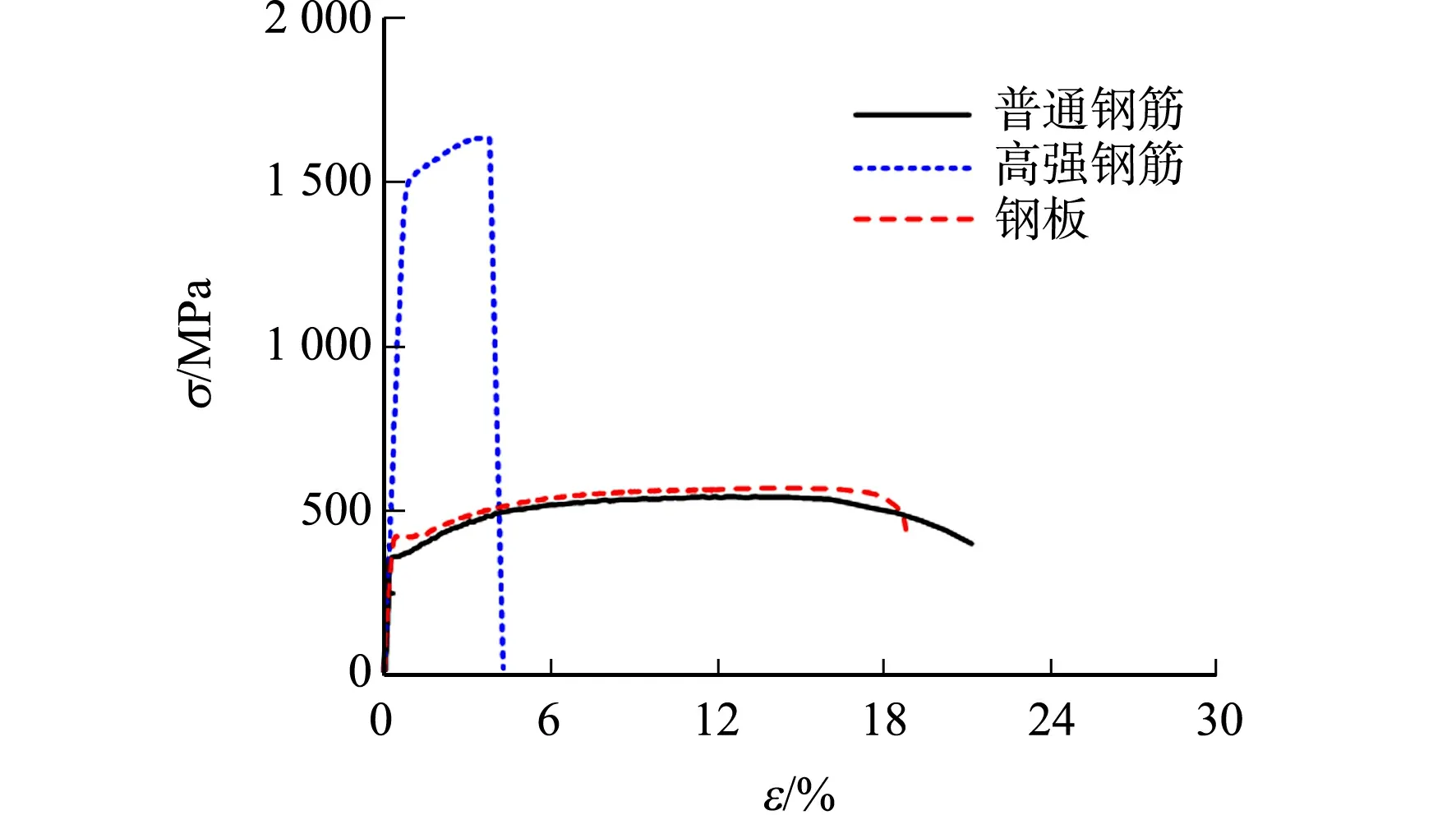
图2 钢材实测应力-应变曲线 Fig.2 Measured stress-strain curves of steel

1.3 加载方案及量测
试验的加载装置和测点布置,如图3所示.图3中:D1~D5为位移计.试验在10 MN压剪试验机下进行,采用两对刀铰对试件进行偏压加载,刀铰转动中心之间的距离为960 mm.在试件正面和背面分别架设一个竖向位移计,用于量测两刀铰之间的竖向位移.试件左面居中布置3个水平位移计,位移计间距为100 mm,用于量测试件的侧向变形.钢管4个侧面均布设应变片,布设高度与3个水平位移计高度一致.在整个加载过程中,以0.01 mm·s-1的速率施加竖向位移.当试件加载至轴力为峰值荷载的50%或轴向位移达到40 mm时,停止加载.

(a) 加载装置 (b) 测点布置 图3 试验的加载装置和测点布置(单位:mm)Fig.3 Test setup loading setup and measuring points arrangement (unit: mm)
2 试验结果与分析
2.1 试验现象
试件的轴向荷载-轴向位移(Pt-δ)曲线,如图4所示.图4中:钢板的受压与受拉屈服通过实测的钢板轴向应变确定;受压侧钢板的初始局部屈曲、受拉侧钢板的断裂及竖向焊缝的开裂等现象通过观察确定;混凝土的压溃和螺旋箍筋的断裂通过加载过程中的声响确定.
所有试件的受压侧钢板的屈服均先于局部屈曲,这是由于内填混凝土限制了钢板的向内变形,钢管混凝土中的钢板可简化为四边固接板进行分析.根据Timoshenko等[12]提出的该类板的弹性局部屈曲应力计算公式,文中试验的弹性屈曲应力(1 500 MPa)远大于屈服强度(423 MPa).因此,所有试件的钢板均先发生屈服.当内填混凝土开始压溃时,试件几乎达到峰值荷载,说明组合柱承载力的下降主要由混凝土压溃导致.试件EC-N-0.32,EC-H-0.32的螺旋箍筋分别在轴向位移约为44,30 mm时发生断裂,表明相同偏心率下高强螺旋箍筋断裂的发生早于普通螺旋箍筋,这可能是由于高强箍筋的延伸率小于普通箍筋的延伸率.在加载末期,试件EC-O-0.32,EC-N-0.32的竖向焊缝发生开裂,试件EC-H-0.32的受拉侧钢板发生断裂.
试件的最终破坏形态,如图5所示.由图5可知:试件的破坏主要集中于弯矩最大的中间段区域,但不同试件破坏的具体位置不同;破坏集中区域的受拉侧混凝土裂缝较宽且比较密集;内配螺旋箍筋试件由于箍筋的约束作用,当加载结束后,其核心混凝土仍具有较好的完整性.

(a) EC-O-0.32 (b) EC-N-0.32 (c) EC-H-0.32图4 试件的轴向荷载-轴向位移曲线Fig.4 Axial load-axial displacement curves of specimens

(a) EC-O-0.32 (b) EC-N-0.32 (c) EC-H-0.32图5 试件的最终破坏形态Fig.5 Final failure modes of specimens
2.2 承载力和延性比
主要试验结果,如表2所示.表2中:Pm为峰值荷载(偏压承载力);dy为屈服位移,是轴向荷载-轴向位移曲线上升段轴力为0.75Pm时的位移的4/3倍[13];dm为峰值位移;du为极限位移,是轴力下降到0.8Pm时的位移;m为延性比,m=du/dy;Mcm为峰值荷载对应的控制截面弯矩.

表2 主要试验结果Tab.2 Primary test results
由表2可知:3个试件的峰值荷载相对差值都在5%以内, 说明螺旋箍筋对组合柱承载力的提高作
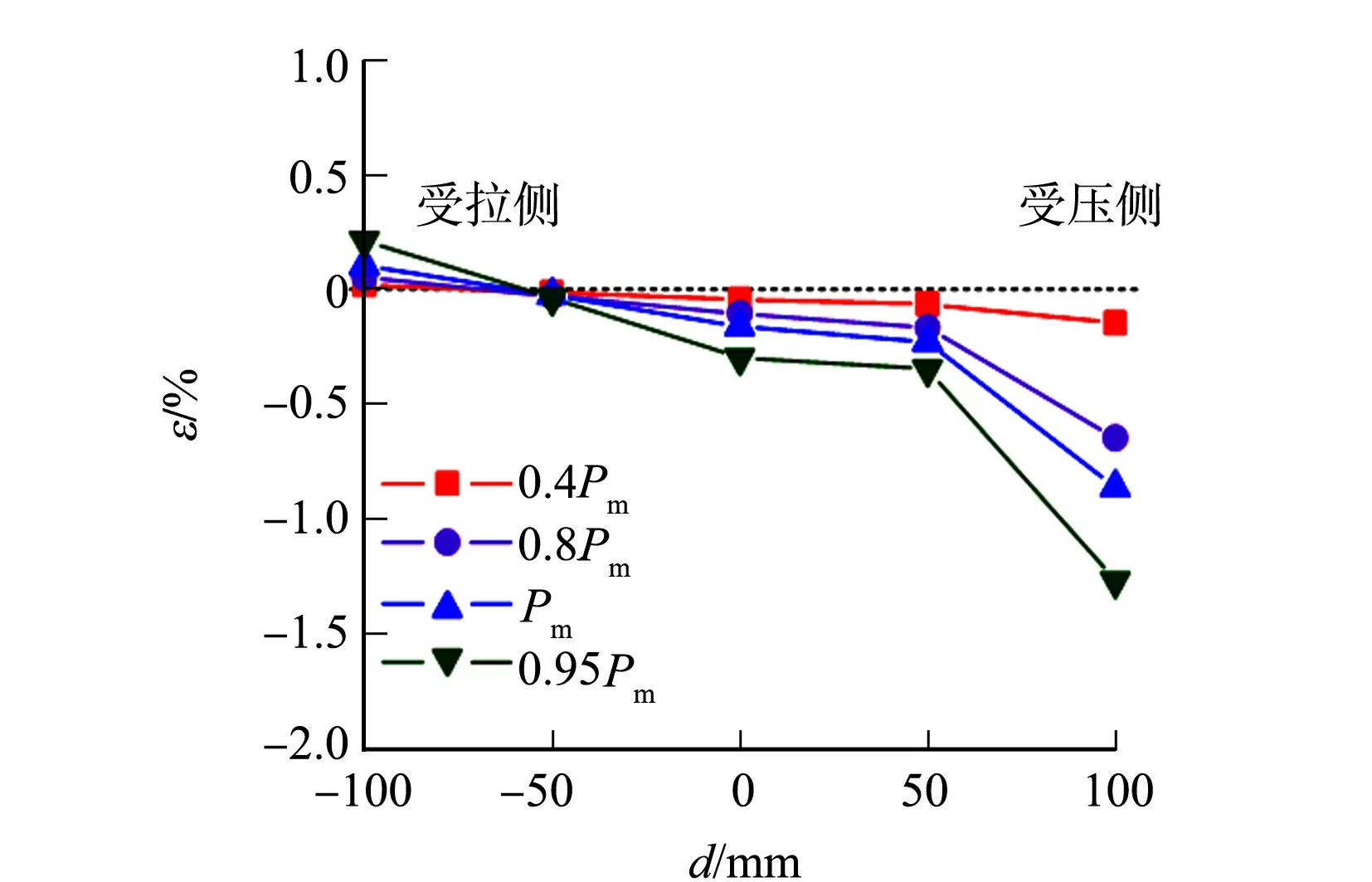
图6 实测钢管应变分布Fig.6 Measured strain distribution of steel pipe
用不明显;螺旋箍筋能够显著提高组合柱的极限位移和延性比;内配普通螺旋箍筋方钢管混凝土柱的延性比约为普通方钢管混凝土柱的2倍,内配高强螺旋箍筋方钢管混凝土柱的延性比约为普通方钢管混凝土柱的3倍.
2.3 控制截面的荷载-变形响应
由于控制截面的荷载-变形响应决定试件的整体受力行为,故对其进行分析.控制截面取3个测量截面中应变发展最快的截面.由于试件存在几何缺陷,混凝土材料性能沿试件高度发生变化,因此,控制截面不一定是试件的中截面.试件EC-O-0.32控制截面的钢板实测应变分布,如图6所示.图6中:d为测点距截面中线的距离.由图6可知:在试验加载初期,钢板应变沿截面高度大致呈线性分布;钢管局部屈曲发生后, 局部屈曲区域的应变量测数据受钢板局部弯曲变形的影响,已不能反映试件的整体变形,但局部屈曲区域外的钢管应变仍大致呈线性分布.基于平截面假定,由整体变形产生的受压边缘应变εce可由对应受拉侧的应变外推得到,继而计算出控制截面的曲率φc.3个试件控制截面的轴向荷载Pt、横向位移Δc、无量纲曲率φcB和截面弯矩Mc(Mc=Pt(e+Δc))随受压边缘应变εce的响应,如图7所示.
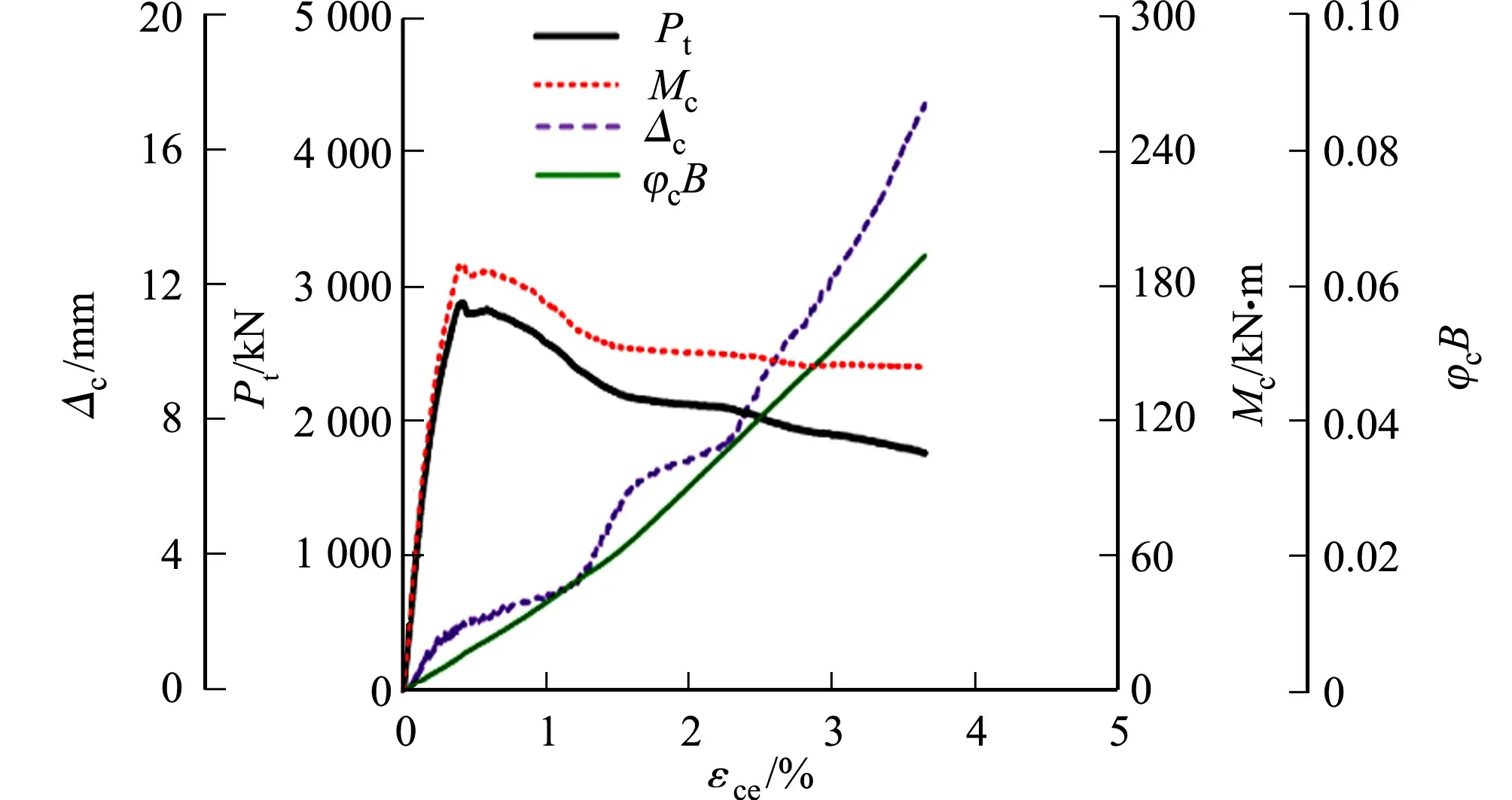
(a) EC-O-0.32

(b) EC-N-0.32 (c) EC-H-0.32 图7 3个试件控制截面的响应Fig.7 Response of control section of three specimens
由图7可知:φcB和εce基本呈线性关系,说明加载过程中中和轴的位置基本不变;当达到峰值荷载时,控制截面的弯矩也几乎达到最大值;由于二阶效应的影响,达到峰值荷载后,截面弯矩Mc的下降速度较轴向荷载更为缓慢,试件EC-H-0.32的截面弯矩Mc在峰值荷载后略有增加.
3 偏压承载力的计算
目前,现有的国内外规范暂无SCCFST柱的偏压承载力计算公式.由上述试验结果可知:螺旋箍筋能有效提高CFST柱的延性,但螺旋箍筋对CFST柱承载力的提高作用不明显.因此,采用已有的方钢管混凝土柱相关规范[14-16]的设计公式预测SCCFST柱的偏压承载力.CFST构件偏压承载力的设计公式,如表3所示.表3中:As,Ac分别为钢管、管内混凝土的截面面积;fy为钢管屈服强度;fck为混凝土轴心抗压强度;P,M分别为竖向力设计值和弯矩设计值;Pn,Mn分别为根据规范ANSI/AISC 360-16计算的CFST柱轴向承载力和弯矩承载力;Pu,Mu分别为根据规范CECS 159:2004计算的CFST柱轴向承载力和弯矩承载力;Pn,EC,Mn,EC分别为根据规范EN 1994-1-1:2004计算的CFST柱轴向承载力和弯矩承载力;ac,μd均为抗弯承载比.
规范EN 1994-1-1:2004采用轴力-弯矩相关曲线计算偏压承载力,相关曲线由4个特征点确定,截面强度承载力通过建立4个特征点间的3条直线方程进行计算.这些计算公式均不考虑材料的分项系数与抗力系数.
由设计公式计算得到的偏压承载力预测值与试验值的对比,如表4所示.表4中:PANSI为根据规范ANSI/AISC 360-16计算得到的偏压承载力预测值;PCECS为根据规范CECS 159:2004计算得到的偏压承载力预测值;PEC为根据规范EN 1994-1-1:2004计算得到的偏压承载力预测值.
由表4可知:规范EN 1994-1-1:2004的偏压承载力预测值与试验结果吻合较好,规范CECS 159:2004,ANSI/AISC 360-16的预测值都偏于保守,且规范ANSI/AISC 360-16的保守性过高.这主要是由于规范ANSI/AISC 360-16计算组合构件偏压承载力的轴力-弯矩相关曲线是基于钢结构的相关曲线,该曲线不考虑轴力对弯矩的增强作用,且这种保守性随着内填混凝土对钢管混凝土承载力贡献比例的增大而增大.

表3 CFST构件偏压承载力的设计公式Tab.3 Design formula of eccentrically loaded capacity of CFST members

表4 偏压承载力预测值与试验值的对比Tab.4 Comparison between predicted and experimental eccentrically loaded capacity
4 结论
对内配螺旋箍筋方钢管超高强混凝土柱的偏压性能进行研究,完成3个试件的偏压试验,其内填混凝土的抗压强度为111 MPa,试验变化参数为螺旋箍筋强度,可得到以下4个结论.
1) 组合柱承载力的下降主要是由混凝土压溃导致.当混凝土开始压溃时,试件也几乎达到峰值荷载.在相同偏心率下,组合柱中高强螺旋箍筋断裂的发生早于普通螺旋箍筋.
2) 局部屈曲区域的应变测量数据不能反映试件的整体变形.基于平截面假定,受压边缘应变可由对应受拉侧的应变外推得到.当达到峰值荷载时,控制截面的弯矩也几乎达到最大值.由于二阶效应的影响,达到峰值后,截面弯矩的下降速度较轴向荷载缓慢.
3) 螺旋箍筋对方钢管超高强混凝土柱的承载力提高作用不明显,但能有效提高组合柱的延性.
4) 规范EN 1994-1-1:2004能够较为合理地预测出内配螺旋箍筋方钢管超高强混凝土柱的偏压承载力.

