隧道下穿民房爆破振动效应监测
朱浩杰, 蔡奇鹏, 肖朝昀, 林立华, 涂兵雄, 黄山景
(1. 华侨大学 土木工程学院, 福建 厦门 361021; 2. 厦门路桥工程投资发展有限公司, 福建 厦门 361021)
暗挖隧道下穿建筑物时,会使爆源附近的建筑物受到一定程度的影响.目前,已有众多学者对爆破振动波在岩土介质中的传播规律及减振技术进行研究,对比分析建筑物的振害特征及其对应的振动观测值,以不同频率段对应的最大振速作为爆破控制标准[1].张声辉等[2]采用小波变换和反应谱分析方法,发现爆破振动信号的能量主要分布在0~64 Hz,随着高程的增加,能量分布趋于低频带.毕卫国等[3]通过对爆破地震波主频小波分析,发现振动主频与结构固有频率越接近,结构响应越大.李洪涛等[4]采用结构动力学理论对工程实例进行分析,发现建筑物对爆破振动不同频率能量成分的选择放大效应,以及结构固有频率一致的能量成分将被最大程度地放大.
工程中以预测振速控制装药量[5-8],爆破最大振速可通过萨道夫斯基公式求出,但在振动传递的过程中,常因其他因素的影响导致实际振速与预测值相差较大.针对下穿隧道,一些学者提出“空洞效应”的概念[9-12],即已开挖的隧道形成空洞后,对地表振速产生放大效应.杨海书等[13]拟合现场实测振动数据,发现隧道空洞对其上部建(构)筑物的振速放大倍数约为2.王辉等[14]分析轻轨隧道下穿建筑物时的爆破振动速度,发现下穿建筑物后的爆破振速放大倍数约为 1.32~1.69.文献[15-16]以掌子面前、后的振速比值和振速差值作为空洞效应衡量指标,探讨掌子面附近的振速变化规律,发现随着距离的增大,指标值先增大后减小.基于此,本文对福建省厦门市石堀山隧道爆破开挖过程中洞顶民房进行长期持续监测,分析民房全过程爆破振动数据,研究“空洞效应”下振速和主频的变化规律.
1 工程概况
福建省厦门市石堀山隧道为双向6车道公路隧道, 该隧道为分离式隧道,左、右线隧道中心线距离约为35 m,施工时,左线先行,前后错开30 m.在隧道右线AK0+400桩号处有一栋两层砖混结构民房,民房高度为7.2 m,第一、二层高度均为3 m,民房的抗拉、抗剪、抗弯能力弱,抗震性能差,施工期间需重点监测爆破振动对其的影响.
在民房第一层(测点1)及第二层(测点2)墙角处,各布置1台自动化爆破振动仪,监测三方向(径向X、切向Y、垂向Z)质点振速及对应的主频.监测时间从2017年1月1日至2017年4月16日,连续监测105 d,共获取238组数据,由此分析民房前、后100 m左线和右线的爆破振动数据.
隧道及民房平面图,如图1所示.右线隧道地质纵断面图,如图2所示.图1,2中:径向X为开挖方向;民房距隧道拱顶为53 m;RQD为岩石质量指标;Kv为岩体完整性系数.
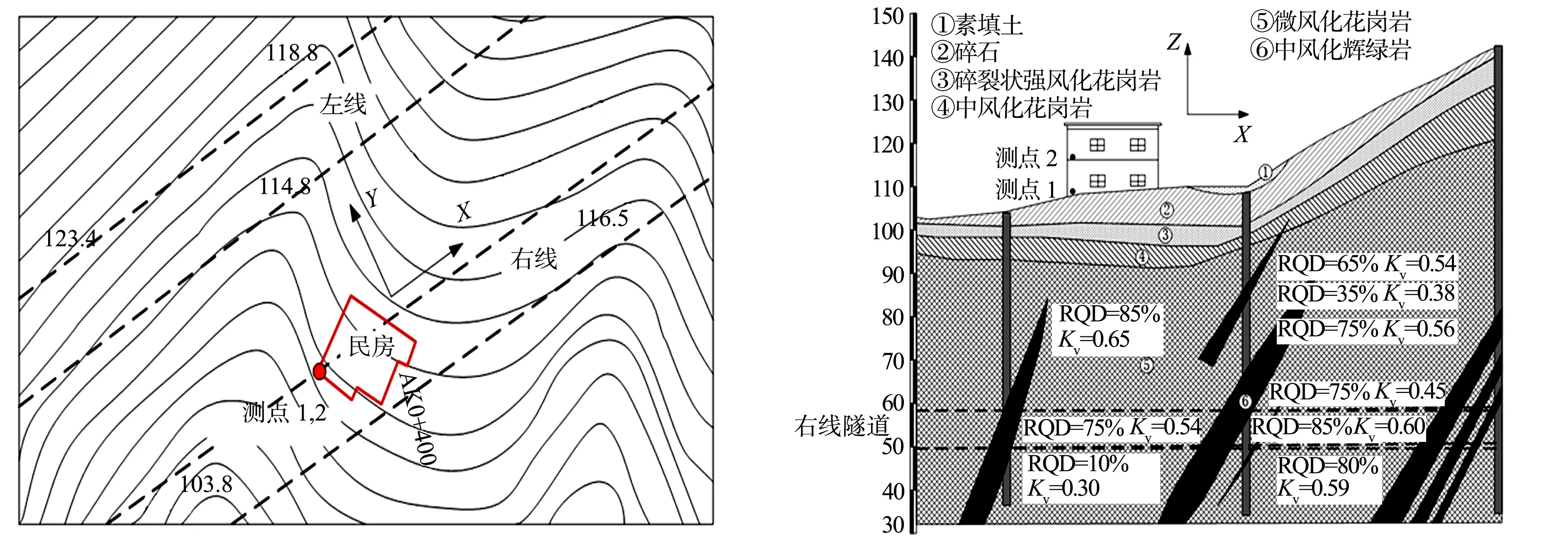
图1 隧道及民房平面图(单位:m) 图2 右线隧道地质纵断面图(单位:m)Fig.1 Plan of tunnel and civil buildings (unit: m) Fig.2 Geologic profile of right line tunnel (unit: m)
2 监测数据分析
以民房为中心,测点与掌子面上方地表处的水平距离记为L,左线和右线隧道爆破振速v与距离L的关系图,如图3,4所示.图3,4中:vX~vZ分别表示径向、切向和垂向的爆破振速.由图3,4可知:爆破振速整体上随着测点与掌子面距离的减小而增大,基本符合萨道夫斯基振速衰减规律.
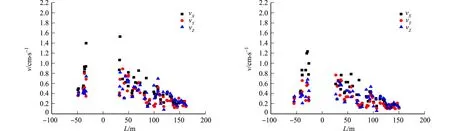
(a) 测点1 (b) 测点2图3 左线隧道爆破振速与距离的关系图Fig.3 Relationship between blasting speed and distance of left line tunnel
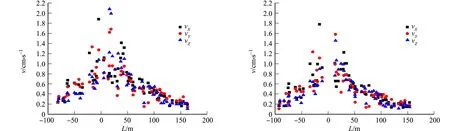
(a) 测点1 (b) 测点2图4 右线隧道爆破振速与距离的关系图Fig.4 Relationship between blasting speed and distance of right line tunnel
在爆破振动三向分量中,普遍认为垂向振速最大[17],因此,进行相关分析时,通常以垂向振速为依据.然而,在文中隧道爆破振动数据中,垂向振速并不是最大,甚至在距离房屋较近的爆破振动中,径向振速明显大于垂向振速,水平向振速明显不可忽视.
在工程统计的238组数据中,有105组数据的径向振速最大,比例为44%;有64组数据的切向振速最大,比例为27%;有69组数据的垂向振速最大,比例为29%.因此,单纯地以垂向振速作为分析依据并不科学.在以民房为中心的50 m范围内的90组数据中,径向振速最大的数据比例为58%,切向振速最大的数据比例为18%,垂向振速最大的数据比例为24%.隧道开挖至测点前4.5 m时,测得径向振速为1.878 cm·s-1,达到预警值.
结构固有频率与振动主频越接近时,结构响应越大[3].参照文献[18-19]的方法,计算隧道上方砌体结构的固有频率.砌体房屋自振周期T与房屋高度H0相关,T=0.016 8×(H0+1.2).该砌体房屋的高度为7.2 m,经计算可得砌体房屋自振周期为0.141 12 s,固有频率f0为7.09 Hz(f0=1/T).
左线和右线隧道测点主频(f)与距离的关系图,如图5,6所示.图5,6中:fX~fZ分别表示径向、切向和垂向主频.由图5,6可知:切向主频最大,大多为35~70 Hz,径向主频次之,大多为35~55 Hz,垂向主频最小,多为15~45 Hz;在238组数据中,小于30 Hz的切向主频为9.2%,径向主频为15.1%,垂向主频为36.6%;距离为50 m以内的90组数据中,小于30 Hz的切向主频为4.5%,径向主频为10.2%,垂向主频为40.9%,切向平均主频为48.83 Hz,径向平均主频为43.58 Hz,垂向平均主频为32.52 Hz,垂向主频处于更小的频带上.
由此可知,垂向主频更接近民房的固有频率,根据不同频率能量成分的选择放大效应[4],垂向振速产生的能量对房屋的影响更大,径向能量次之,切向能量最小.因此,在单一分向振速并不一直占据优势时,可以综合优势振速与主频选取分析对象,选择优势分向振速或根据建筑物固有频率选择较为接近主频的分向振速进行分析.

(a) 测点1 (b) 测点2图5 左线隧道测点主频与距离的关系图Fig.5 Relationship between main frequency and distance of left line tunnel measuring point
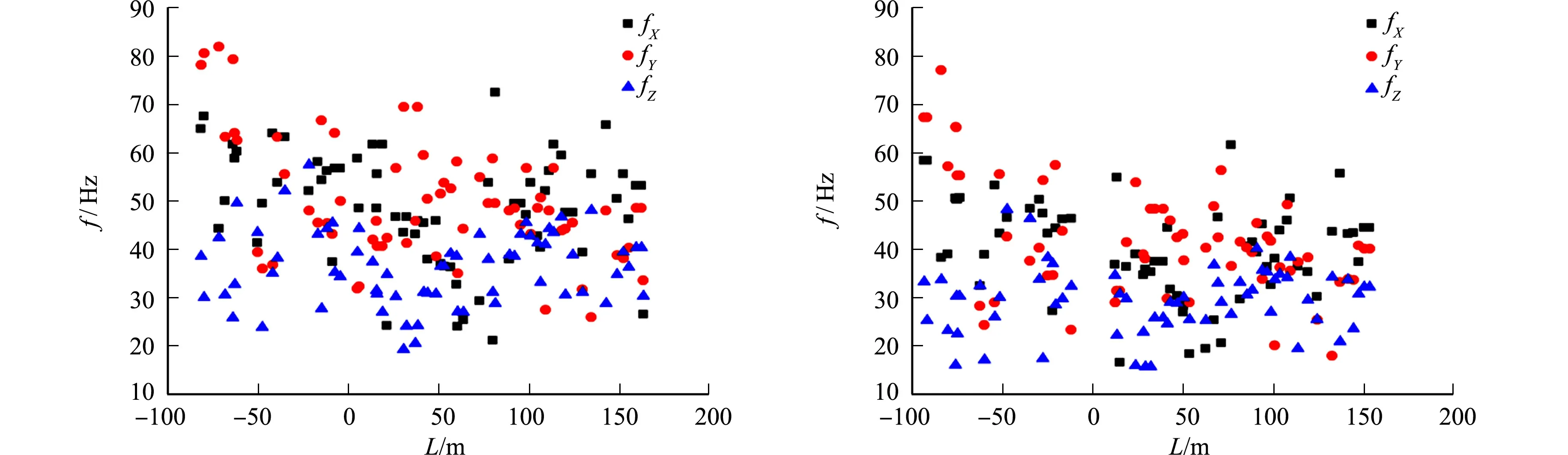
(a) 测点1 (b) 测点2图6 右线隧道测点主频与距离的关系图Fig.6 Relationship between main frequency and distance of right line tunnel measuring point
3 空洞效应分析
对于钻爆法隧道施工,众多学者以掌子面为对称面,对比未成洞前和成洞后的爆破振速,发现隧道已开挖成洞区地表的振速比对称位置未开挖区地表的振速更大,从而提出空洞效应的概念[9-12].以房屋为对称点,在相同药量和距离的情况下,对比掌子面未通过房屋时与通过房屋后的数据,分析空洞产生的影响.
右线隧道下穿前、后测点的振速对比,如图7所示.图7中:v1,-X表示掌子面在测点后方的测点1的径向振速;v1,+X表示掌子面在测点前方的测点1的径向振速;下文下标表示类似.
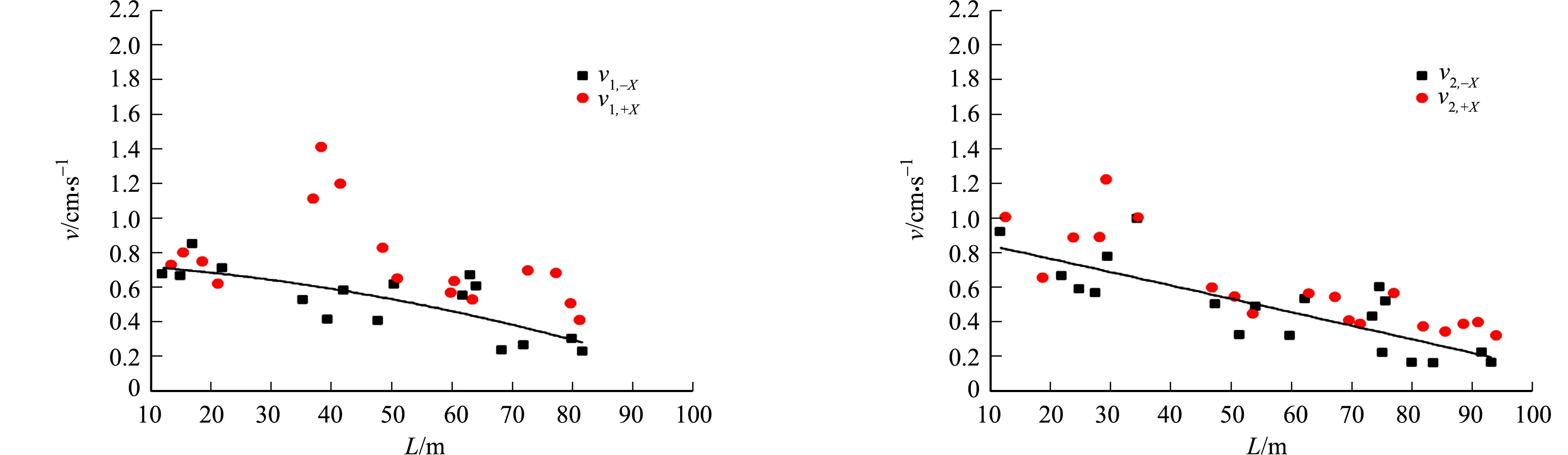
(a) 测点1(径向) (b) 测点2(径向)
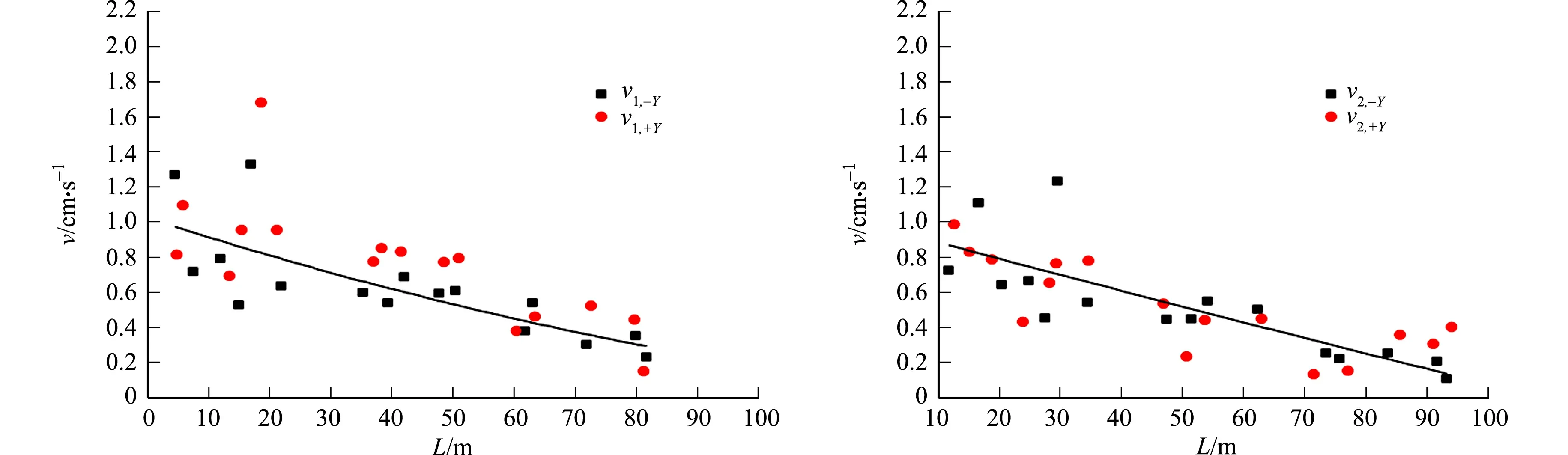
(c) 测点1(切向) (d) 测点2(切向)
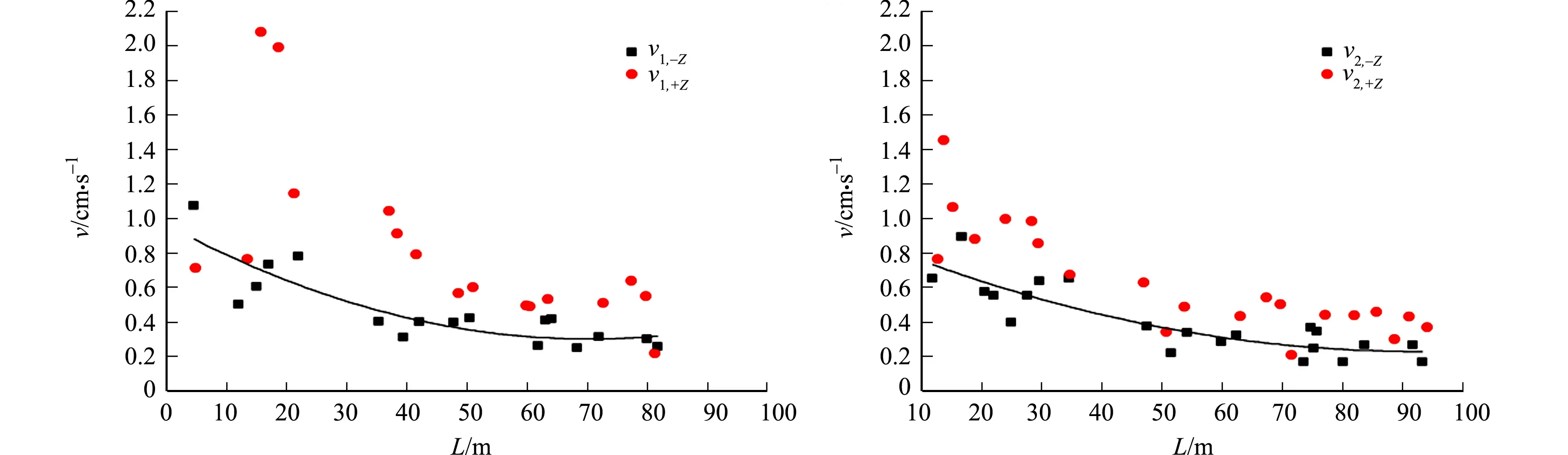
(e) 测点1(垂向) (f) 测点2(垂向)图7 右线隧道下穿前、后测点的振速对比Fig.7 Comparison of vibration velocity of measuring points before and after right line tunnel undercrossing
由图7可知:回归曲线拟合测点前方,即空洞形成前,三向振速均随距离的增加而降低;空洞形成后,测点1的径向、垂向振速明显增大,测点2的垂向振速略有增大,径向和切向振速变化不大;工程的放大效应随楼层的增加而减弱.
测点1的径向、垂向振速变化的最大幅值并不是出现在距离测点最近的位置,而是一个从小到大再变小的过程.对比未形成空洞时测点1的垂向振速,在空洞形成后15.7 m处,垂向振速显著增大,振速达2.08 cm·s-1,超过GB 6722-2014《爆破安全规程》的限值[1].
在一定的地质条件下,离测点相同距离时,不同爆破作业在测点处测得的主频基本相同[20-21].右线隧道下穿前、后测点的主频对比,如图8所示.由图8可知:空洞会使主频衰减;主频在距测点一定范围内有所衰减,测点2在10~40 m内的径向和垂向主频衰减至15 Hz左右.
曹孝君[16]以掌子面为对称面,通过隧道中轴线上已开挖区(成洞区)与对称于爆源的未开挖区的地表质点振速之比(空洞效应的振速放大系数)衡量爆破振动的空洞效应.由于空洞效应不仅会对振速产生影响,而且还会显著影响主频,故重新定义空洞影响系数,即振速影响系数Cv和主频影响系数Cf,分别对应于以房屋为对称点,用开挖至测点后方爆破在测点位置产生的振速(主频)与未开挖至测点时爆破在测点产生的振速(主频)之比.
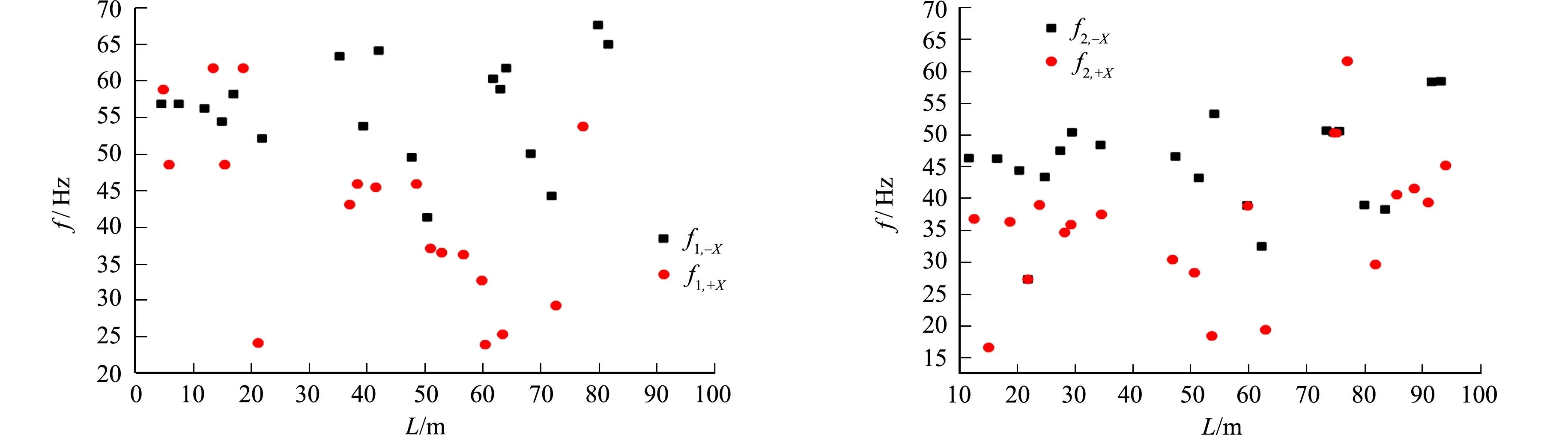
(a) 测点1(径向) (b) 测点2(径向)
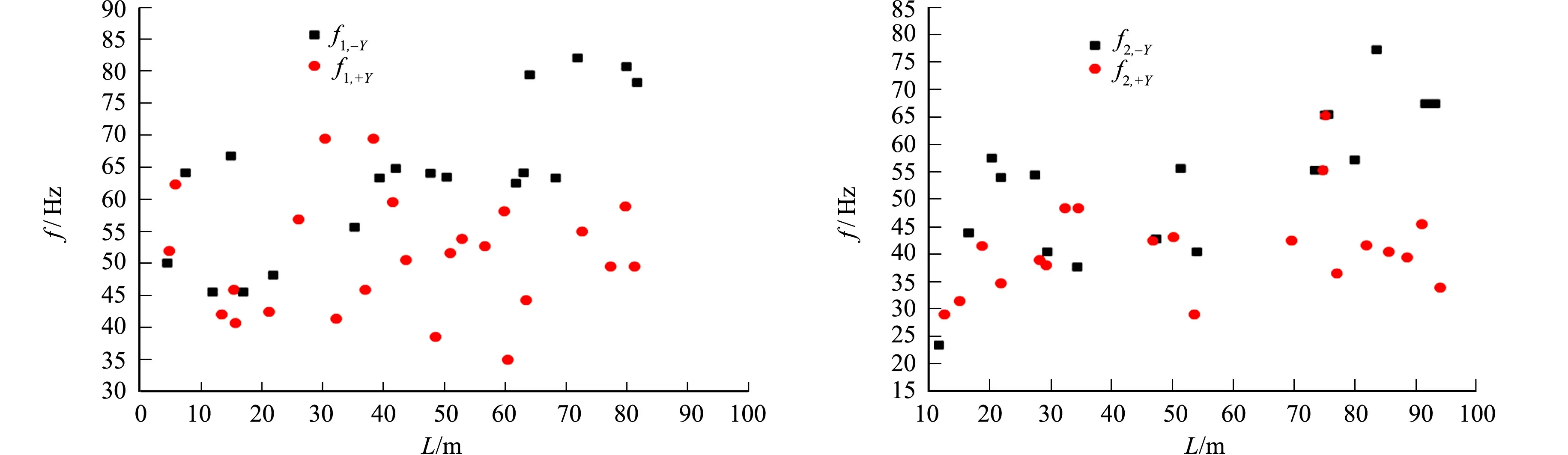
(c) 测点1(切向) (d) 测点2(切向)
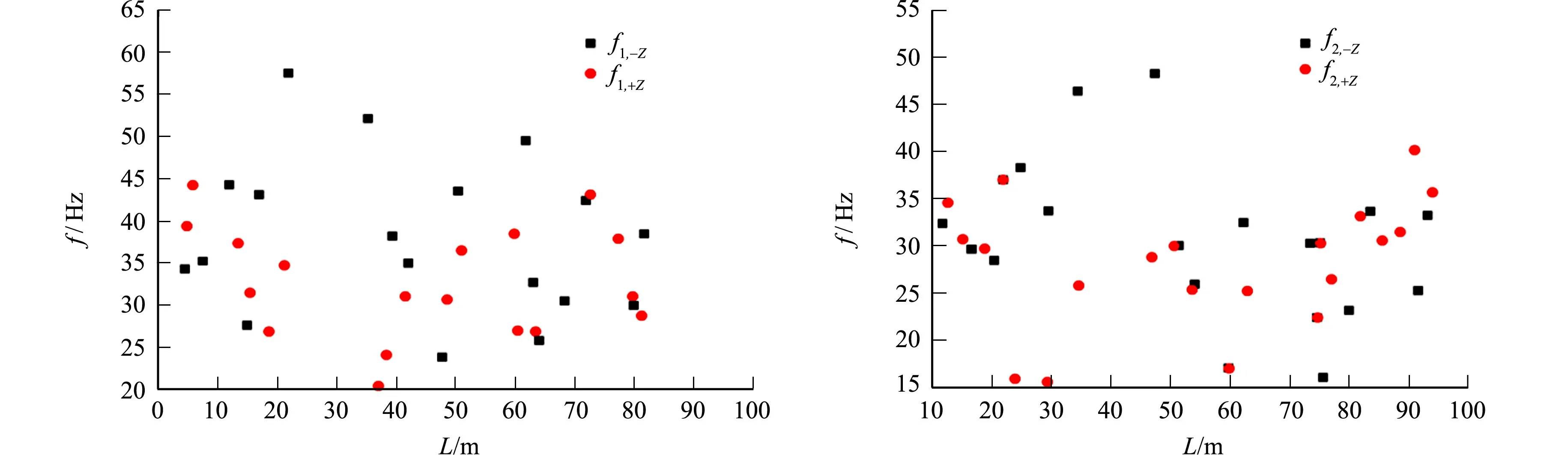
(e) 测点1(垂向) (f) 测点2(垂向)图8 右线隧道下穿前、后测点的主频对比Fig.8 Comparison of main frequency of measuring points before and after right line tunnel undercrossing
因此,振速影响系数Cv和主频影响系数Cf的计算式分别为
Cv=vb/vf,Cf=fb/ff.
式中:vf为未形成空洞前测得的振速;vb为形成空洞后测得的振速;ff为未形成空洞前测得的主频;fb为形成空洞后测得的主频.
当距离小于50 m时,振速较大;当距离超过50 m时,振速已普遍降低至0.6 cm·s-1以下(图7).距离小于50 m时,振速影响系数与主频影响系数的变化图,如图9所示.图9中:Cv,1,X,Cf,1,X分别表示测点1的径向Cv,Cf值;其他表示类似.由图7,9可得以下2个结论.
1) 振速影响系数大致呈现出“中间大,两头小”的特征,表明空洞形成后,放大作用随着掌子面距测点距离的增加而先增大后减小;当距离为20~50 m时,测点1放大系数较大,径向和垂向系数接近,普遍超过2,径向系数最大超过3,切向系数在1.5左右波动;当距离小于25 m时,垂向振速相对未形成空洞之前,增加了1.257 cm·s-1,达2.182 cm·s-1,超过控制值2.0 cm·s-1;当距离为30~50 m时,径向振速放大明显,增幅最大为0.997 cm·s-1;当距离为10~50 m时,测点2垂向最大放大系数也超过2.0.结合放大系数和增加幅值可知,垂向振速放大最大,径向振速次之,切向振速最小,第一层比第二层的振速放大效应更大.

(a) 测点1(径向) (b) 测点2(径向)

(c) 测点1(切向) (d) 测点2(切向)

(e) 测点1(垂向) (f) 测点2(垂向)图9 振速影响系数与主频影响系数的变化图Fig.9 Variation between influence coefficient of vibration velocity and main frequency
2) 空洞形成后,在50 m范围内,两个测点上的三向主频均有不同程度的降低,主频影响系数Cf大多数均小于1,存在先减小后增大的过程;测点1的垂向Cf最小值为0.39,测点2的垂向Cf最小值为0.41;测点1的径向Cf最小值为0.46,测点2的径向Cf最小值为0.35;测点1切向Cf最小值为0.68,测点2的切向Cf最小值为0.60.总体而言,主频影响系数垂向最小,径向次之,切向最大.
当振速较大时,特别是振动主频越接近建筑物固有频率时,会对建筑物造成损害[3-4].空洞的存在会导致振速增加,主频减小.例如,由于空洞的存在,测点1的垂向振速增加幅值较大,而此时主频影响系数为0.39,主频小于20 Hz,接近房屋的固有频率7.09 Hz,其他方向也普遍存在此类情况.工程右线隧道从民宅正下方穿过,施工单位应严格控制爆破装药量,控制爆破振速,除了个别点垂向振速超过2.0 cm·s-1外,3个方向测得的振速均控制在1.6 cm·s-1以下.在隧道下穿房屋之前,仅民房窗台处出现个别细小裂缝,隧道下穿至工程结束后,民房窗台、墙壁开裂严重.因此,在爆破工程中,不能仅考虑隧道开挖至建筑物前的过程,就认为隧道通过后建筑物是安全的;而是应当充分认识空洞效应对振速放大、主频减小的影响,对空洞形成后的爆破控制,更要严格把控,尽可能减少对建筑物的损害.
4 结论
基于福建省厦门市石堀山隧道下穿民房段的大量自动化监测数据,详细分析振速及主频的变化规律,得出以下4个结论.
1) 爆破振速整体上随着测点与掌子面距离的减小而增大.在238组数据中,径向分量最大振速占比最多,达44%;主频小于30 Hz的分量中,垂向分量占比最多,达36.6%.三向振速中,垂向振速不一定总是最大,应综合振速与主频,选择优势分向振速或根据建筑物固有频率选择接近的主频对应的分向振速进行相关分析.
2) 隧道后方形成空洞后,在10~50 m范围内,将显著放大爆破振动速度,振速增幅最大达1.257 cm·s-1,而主频有一定的衰减,径向和垂向主频衰减至与房屋固有频率接近.
3) 重新定义空洞影响系数,引入振速影响系数Cv和主频影响系数Cf描述空洞形成前后爆破振动的变化规律.在50 m范围内,随着掌子面远离测点,Cv先增加后减小,而Cf先减小后增大.对于空洞影响的综合效应,垂向最大,径向次之,切向最小.Cv最大值达3.4,Cf最小值为0.35.
4) 隧道下穿民宅时,不能仅仅考虑隧道开挖至建筑物前的过程,就认为隧道通过后建筑物是安全的,应充分认识到空洞效应对振速放大,主频减小的影响.对空洞形成后的爆破控制,更要严格把控,尽可能减少对建筑物损害.

