饱水砂性地层隧道掌子面稳定性分析

■董学绸

(福建省交通规划设计院，福州 350004)

0 引言

饱水砂性地层是一种典型不良地质条件，其结构松散，孔隙率大，透水性强，黏聚力小，自稳性差，掌子面稳定问题成为隧道施工中的重要问题。尤其是在高水压条件下，渗流作用将严重影响饱水砂性地层隧道掌子面稳定性。

针对隧道掌子面稳定性问题，相关学者开展了一些研究工作。Anagnostou等[1]基于三维楔形体模型提出了考虑地下水渗流的掌子面极限支护力计算方法。秦建设[2]采用有限差分程序FLAC3D研究了掌子面变形与破坏机理。胡欣雨[3]采用二维颗粒离散元程序PFC2D研究了不同地层条件下掌子面失稳破坏模式。童建军[4]针对厦门翔安海底隧道饱水砂性地层围岩稳定问题进行了模型试验研究。李君[5]通过室内试验研究了干砂地层中掌子面稳定性问题。已有研究多集中于无水条件下掌子面稳定性方面；对于饱水条件下，尤其是渗流条件下砂性地层隧道掌子面稳定性的研究较少，而采用离散元法对渗流条件下砂性地层隧道掌子面稳定性问题的研究尚未见文献报道。

本文根据饱水砂性地层的物理力学特性，采用离散元流固耦合方法，建立掌子面稳定性研究数值分析模型，从细观尺度对渗流条件下饱水砂性地层隧道掌子面失稳破坏规律和掌子面极限支护压力进行研究。

1 数值分析模型

本文以某隧道穿越高水压砂性地层为工程背景，采用洞径10m的隧道为研究对象，模型尺寸为横向25m，纵向35m，竖向55m。数值分析模型如图1所示。饱水砂性地层物理力学参数如表1所示[6-7]。

图1 数值分析模型

表1 饱水砂性地层物理力学参数

在计算中，假定含水体具有稳定的补给源；隧道采用全断面一次开挖后立即施作支护结构，在掌子面上施加初始支护压力并逐渐减小，研究支护压力变化对掌子面稳定性的影响。根据有效应力原理[8]，当掌子面不排水时，掌子面支护压力为总支护压力 (有效支护压力与初始静水压力之和)；当掌子面排水时，掌子面支护压力为有效支护压力(土骨架间的作用力与渗流产生的渗透力之和)。

2 掌子面失稳破坏规律

选取排水和不排水的典型工况，研究不同排水条件下支护压力变化对掌子面稳定性的影响。在计算中，掌子面中心的初始竖向压力为0.45MPa，初始侧向压力为0.3MPa，初始静水压力为0.6MPa。

2.1 极限支护压力的确定

隧道开挖后，围岩发生卸载，出现向隧道内的变形。在计算中，通过监测掌子面中心的水平位移 (以下简称“掌子面位移”)，得到掌子面位移随掌子面支护压力变化曲线如图2和图3所示。

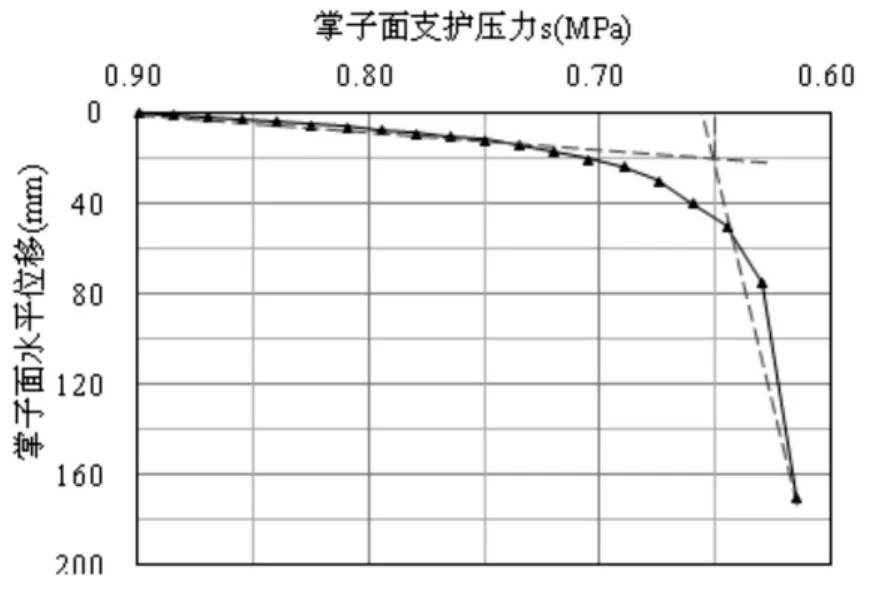
图2 不排水工况掌子面位移随支护压力变化曲线

图3 排水工况掌子面位移随支护压力变化曲线

由图2和图3可知，不同排水条件下，掌子面位移均随掌子面支护压力的减小而增大，且存在突变现象，并具有明显的阶段性。本文将掌子面位移随掌子面支护压力变化曲线发生突变时的掌子面支护压力确定为极限支护压力，并将掌子面位移随掌子面支护压力的变化过程分为以下三个阶段：

(1)线性阶段

当掌子面支护压力远大于极限支护压力时，曲线近似直线，掌子面位移与掌子面支护压力大致呈线性关系，随着掌子面支护压力的减小，掌子面位移缓慢增大，说明围岩发生局部失稳破坏。

(2)敏感阶段

当掌子面支护压力略大于极限支护压力时，曲线逐渐弯曲，掌子面位移与掌子面支护压力不再呈线性关系，随着掌子面支护压力的减小，掌子面位移迅速增大，说明围岩失稳破坏范围扩大。

(3)破坏阶段

当掌子面支护压力等于极限支护压力时，曲线发生突变，随着掌子面支护压力的减小，掌子面位移急剧增大，说明围岩发生整体失稳破坏。

通过上述分析，可以得到不同排水条件下饱水砂性地层掌子面极限支护压力如表2所示。由表2可知，极限有效支护压力远小于初始静止土压力；排水时极限支护压力约为不排水时极限支护压力的30%，说明采取适当的排水措施可以显著降低掌子面极限支护压力，使得高水压条件下的极限支护压力满足实际工程的允许值 (如盾构法常规带压进舱换刀的进仓压力一般不超过0.45MPa)[9]。

表2 不同排水条件下极限支护压力(单位：MPa)

2.2 掌子面失稳破坏模式

但需要注意，在高水压条件下，渗流作用将严重影响饱水砂性地层隧道掌子面稳定性。因此，下面着重探讨排水条件下掌子面失稳破坏模式。排水条件下，不同掌子面支护压力的地层变形分布如图4所示。

由图4可知，随着掌子面支护压力的减小，变形影响范围由掌子面向地表逐渐发展：如图4-(a)所示，当掌子面支护压力较大时，掌子面附近围岩产生变形，发生局部失稳破坏；如图4-(b)～(c)所示，随着掌子面支护压力的减小，变形影响范围逐渐向掌子面前方和上方发展，失稳破坏范围扩大；如图4-(d)所示，当掌子面支护压力小于极限支护压力时，变形程度和影响范围急剧增大，掌子面发生整体失稳破坏，掌子面前方破坏形状表现为楔形状，掌子面上方破坏形状表现为烟囱状。结合不同掌子面支护压力下地层变形的分布规律，可以认为排水条件下饱水砂性地层掌子面失稳破坏区域由掌子面前方滑动破坏区(楔形状)和上方松动破坏区(烟囱状)组成。掌子面失稳破坏模式如图5所示。

3 掌子面极限支护压力计算方法

本文根据掌子面失稳破坏模式，采用考虑渗流的三维楔形体模型[1]，建立排水条件下饱水砂性地层隧道掌子面极限支护压力的计算方法。计算模型如图6所示。掌子面有效极限支护压力可按式(1)计算：

图4 不同掌子面支护压力的地层变形分布图(单位：m)

图5 掌子面失稳破坏模式

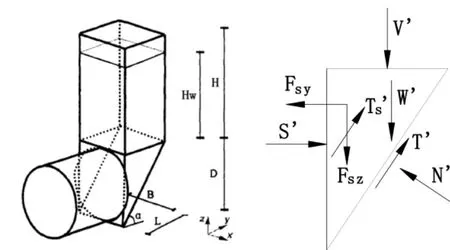
图6 考虑渗流的三维楔形体模型及楔形体受力示意图

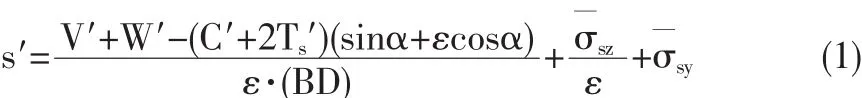
式中：V′为楔形体上方竖向力；W′为楔形体自重；α为楔形体倾角；B为楔形体宽度；D为隧道直径；为水平渗透压力。

水平渗透压力可按式(2)计算：

式(1)中第一项为不考虑渗流时的掌子面极限有效支护压力，可采用理论计算得到；第二项和第三项为渗流时的掌子面渗透压力，渗透力与掌子面附近总水头分布有关，但由于掌子面附近渗流边界复杂，难以给出总水头分布的解析解。因此，本文采用离散元流固耦合方法，研究稳态渗流条件下掌子面附近渗流场分布规律，进而得到作用于楔形体的渗透力。

3.1 渗流场分布规律

通过稳态渗流数值计算得到不同水深(40m、60m、80m、100m)的渗流场分布。水深40m和100m时的隧道纵向总水头等值线如图7所示。由图7可知，不同水深条件下渗流场分布规律相似：隧道开挖后，掌子面附近渗流边界发生改变，地层中渗流场重新分布，掌子面附近水力梯度较大，且水力梯度的水平分量远大于竖向分量，表明水平渗透力远大于竖向渗透力，因此本文仅考虑水平渗透力对掌子面稳定性的影响。

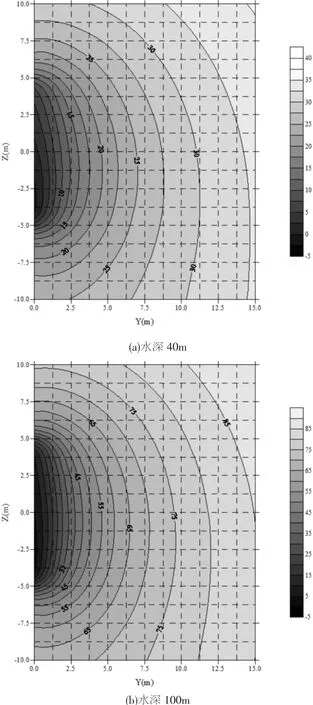
图7 隧道纵向总水头等值线(单位：m)

掌子面中心相对水头沿隧道纵向相对距离变化曲线如图8所示。由图8可知，不同水深条件下各曲线基本重合，拟合得到掌子面中心纵向总水头的表达式(2)，并以此计算作用于楔形体的水平渗透力。研究表明[1]，稳态渗流时埋深对渗流场的影响很小，因此式(2)可适用于不同埋深的情况。

图8 掌子面中心相对水头沿纵向相对距离变化曲线

式中：a=1.397，其余符号同式(1)。

3.2 水平渗透压力

不同有效内摩擦角条件下，相对渗透压力(水平渗透压力与初始静水压力之比)随相对水深变化曲线如图9所示。由图9可知，作用于楔形体的水平渗透压力约为初始静水压力30%左右。

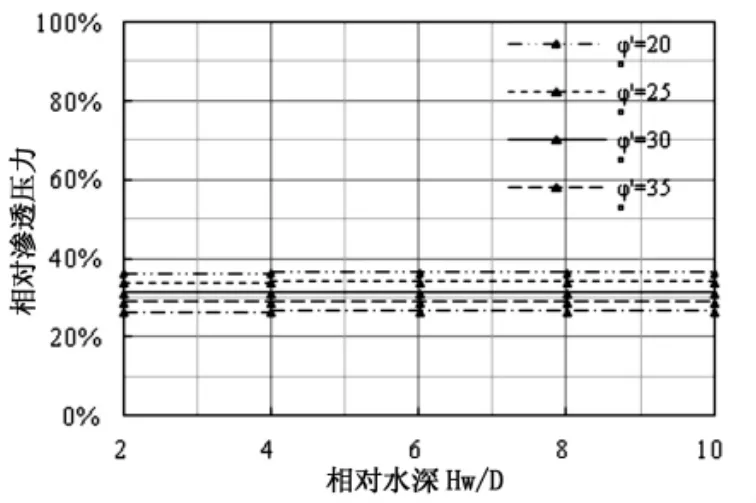
图9 相对渗透压力随相对水深变化曲线

3.3 计算方法

通过上述分析，可以建立渗流条件下饱水砂性地层隧道掌子面极限支护压力的计算方法，即按下述方法分别求得极限有效支护压力的两个组成部分：(1)不考虑渗流时的掌子面极限有效支护压力 (通过不考虑渗流的三维楔形体模型计算获得)；(2)渗流时的掌子面渗透压力(通过稳态渗流数值计算获得)。表3给出了水深60m情况下理论解与数值解的对比。

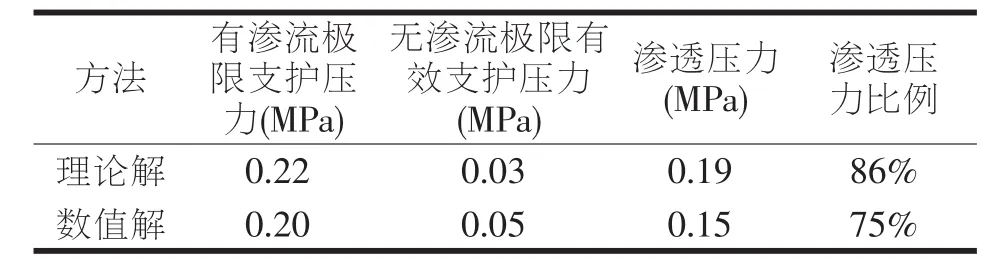
表3 排水条件下饱水砂性地层掌子面极限支护压力

由表3可知，采用理论解与数值解得到的掌子面极限支护压力及其各组成部分的值基本一致，说明本文提出的渗流条件下饱水砂性地层隧道掌子面极限支护压力的计算方法是合理的。同时可以发现，掌子面渗透压力占极限支护压力的比例较大，说明渗透压力是极限支护压力的主要部分。显然，随着水深的增大，渗透压力占极限支护压力的比例逐渐增大，渗透压力(渗流作用)将严重影响饱水砂性地层隧道掌子面的稳定性。

4 结论

本文根据饱水砂性地层的物理力学特性，采用离散元流固耦合方法，建立掌子面稳定性研究数值分析模型，从细观尺度对渗流条件下饱水砂性地层隧道掌子面失稳破坏规律和掌子面极限支护压力进行研究，并从掌子面失稳破坏模式出发采用考虑渗流的三维楔形体理论计算模型，建立了渗流条件下饱水砂性地层隧道掌子面极限支护压力的计算方法。主要研究结论如下：

(1)掌子面极限支护压力的确定

不同排水条件下，掌子面位移均随掌子面支护压力的减小而增大，其变化过程分为三个阶段：①线性阶段，围岩发生局部失稳破坏；②敏感阶段，围岩失稳破坏范围扩大；③破坏阶段，当掌子面支护压力等于极限支护压力时，曲线发生突变，围岩发生整体失稳破坏。

(2)排水条件下饱水砂性地层隧道掌子面失稳破坏模式

排水条件下饱水砂性地层掌子面失稳破坏区域由掌子面前方滑动破坏区(楔形状)和上方松动破坏区(烟囱状)组成。

(3)排水条件下饱水砂性地层隧道掌子面极限支护压力计算方法

考虑渗流的掌子面极限有效支护压力由两部分组成：①不考虑渗流时的掌子面极限有效支护压力(通过不考虑渗流的三维楔形体模型计算获得)；②渗流时的掌子面渗透压力(通过稳态渗流数值计算获得)，作用于楔形体的水平渗透压力一般为初始静水压力的30%左右。