上软下硬地层隧道掌子面稳定性及塌方形态

安永林，李佳豪，曹 前，岳 健，欧阳鹏博

(1.湖南科技大学 岩土工程稳定控制与健康监测省重点实验室，湖南 湘潭 411201;2.湖南科技大学 土木工程学院，湖南 湘潭 411201;3.长沙市轨道交通集团有限公司，湖南 长沙 410000)

在地层应力作用下，地层往往呈现不同程度的风化，通常上部为全风化或者强风化，下部为弱风化。若隧道通过此复合地层，则掌子面会遇到上软下硬的情况，隧道开挖会造成围岩变形受力不均匀，施工不慎或支护不当会引起塌方，如土家湾隧道[1]。

国内外学者对复合地层以及盾构开挖面支护力做了相关研究：Rui Carrilho Gomes[2]利用数值软件模拟分析了2种地层条件下隧道地震响应；Salvador Senent[3]基于极限分析法讨论了层状地层中隧道局部塌方可能性；kos Tóth[4]统计分析了隧道掘进机TBM掘进速率与复合地层的关系； K.M. Neaupane[5]基于神经网络预测了复合地层变形。Wenkai Feng[6]基于FLAC3D建模研究了软硬地层围岩的变形规律。Broms[7]总结了开挖面坍塌破坏和鼓出破坏与地表超载以及地层强度参数的关系，并提出了隧道稳定系数的概念，Davis[8]进一步应用极限分析法分析了4种破坏模式下的隧道稳定系数的上、下限解；Anagnostou G[9]构建了开挖面仓筒破坏模式，并基于极限平衡法推导了开挖面支护力公式；刘招伟[10]讨论了穿越长江水下软硬不均地层隧道修建技术；熊良宵[11]基于数值仿真分析了隧道开挖面接近地质界面时围岩位移特征及其影响因素；王国富[12]研究了突变地质界面盾构隧道开挖面极限支护压力；邱龑[13]分析了富水砂层盾构隧道开挖面稳定性及其失稳风险。上述文献从不同层面对复合地层隧道以及盾构隧道做了分析，但是很少对复合地层矿山法隧道掌子面的稳定进行研究。

本文主要对上软下硬地层隧道掌子面的稳定性及塌方形态进行研究，首先定义掌子面软弱地层相对厚度系数a无量纲参数；然后应用强度折减有限元法，研究不同a下掌子面稳定安全系数及其塌方形态，分析掌子面的变形和地表沉降槽形状，讨论掌子面应力拱效应与传递路径；提出结合强度折减有限元法，用虚拟支护力研究新奥法隧道掌子面的稳定，并同有限元模拟结果、实验结果做对比分析；最后对影响掌子面稳定的因素做参数分析。

1 数值模型及掌子面软弱地层相对厚度系数

1.1 数值模型

武广客运专线浏阳河隧道DIIK1562+793—DIIK1562+960里程段，开挖方法是三台阶法，在上台阶掌子面存在上软下硬地层情况，上部为填土层，下部为弱风化泥质粉砂岩。三维有限元模型的长×宽×高为50 m×70 m×50 m，取掌子面位于掘进10 m处。围岩采用实体单元模拟，因为重点是分析掌子面的稳定性，特别是掌子面塌方的情况，所以认为支护段为同步支护且是刚性的[11]。模型采用的边界条件：模型四周及底面采用法向约束，模型顶面为自由面。建立的数值模型如图1所示。力学参数见表1。

图1 数值模型(单位:m)

表1 计算力学参数

1.2 掌子面软弱地层相对厚度系数

软硬地层分界以及隧道位置如图2所示。图中：H软为软弱地层厚度；H为掌子面开挖高度；δ为拱顶覆土厚度。为了分析不同软弱地层厚度(即软硬地层分界位置不同)对掌子面稳定性的影响，定义掌子面软弱地层相对厚度系数a无量纲参数，其计算公式为

(1)

图2 地层软硬分界

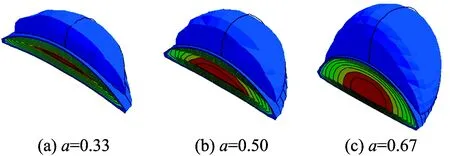
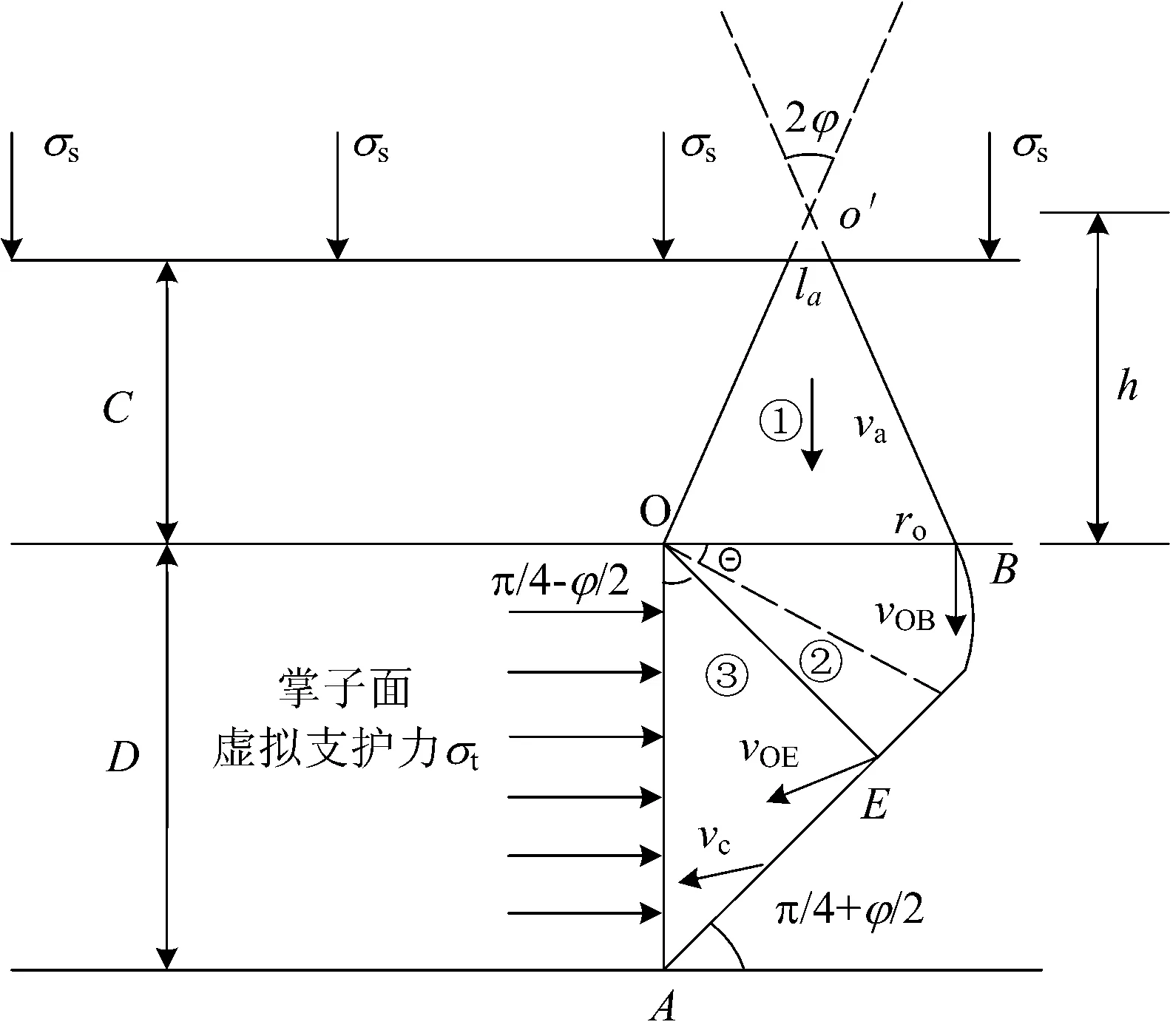
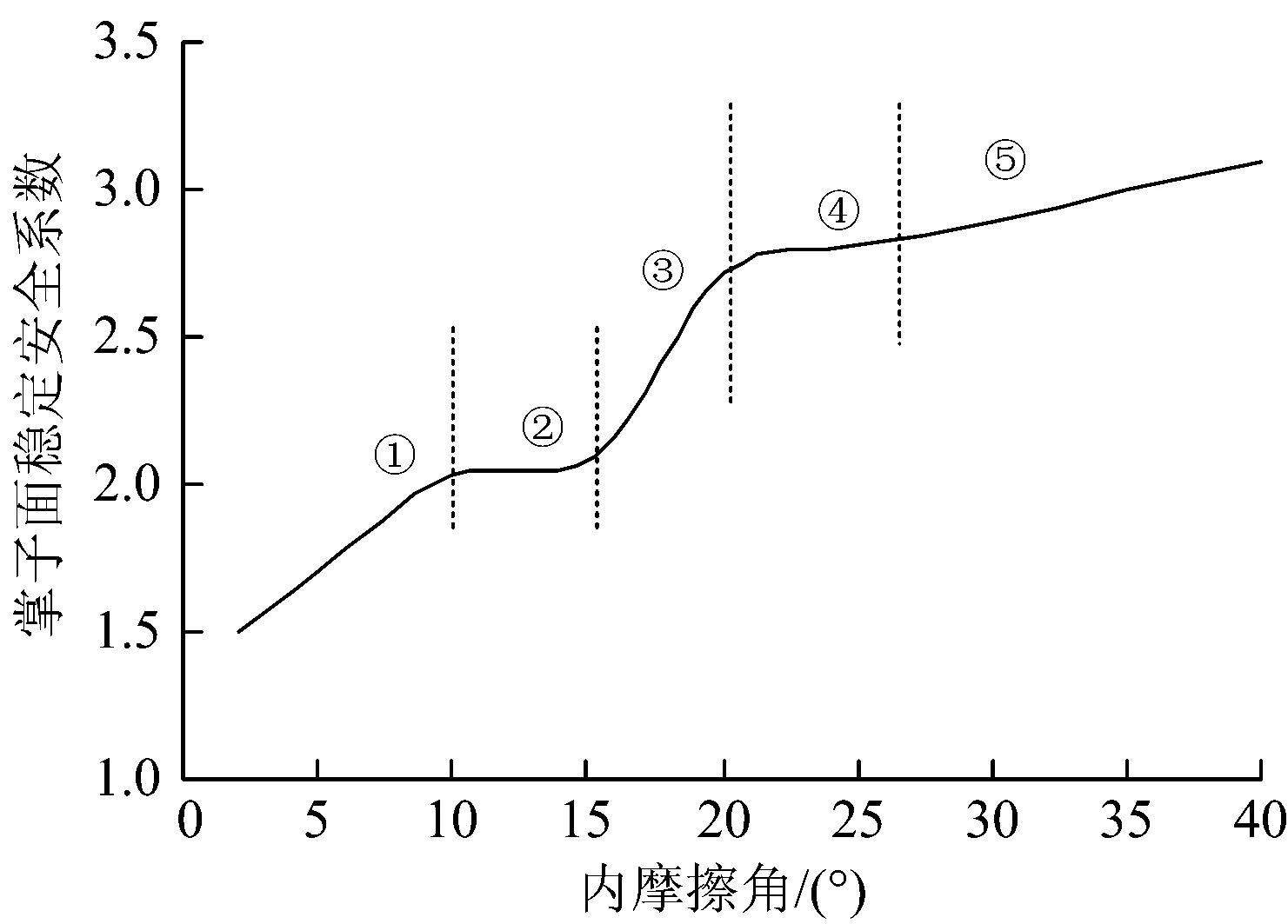
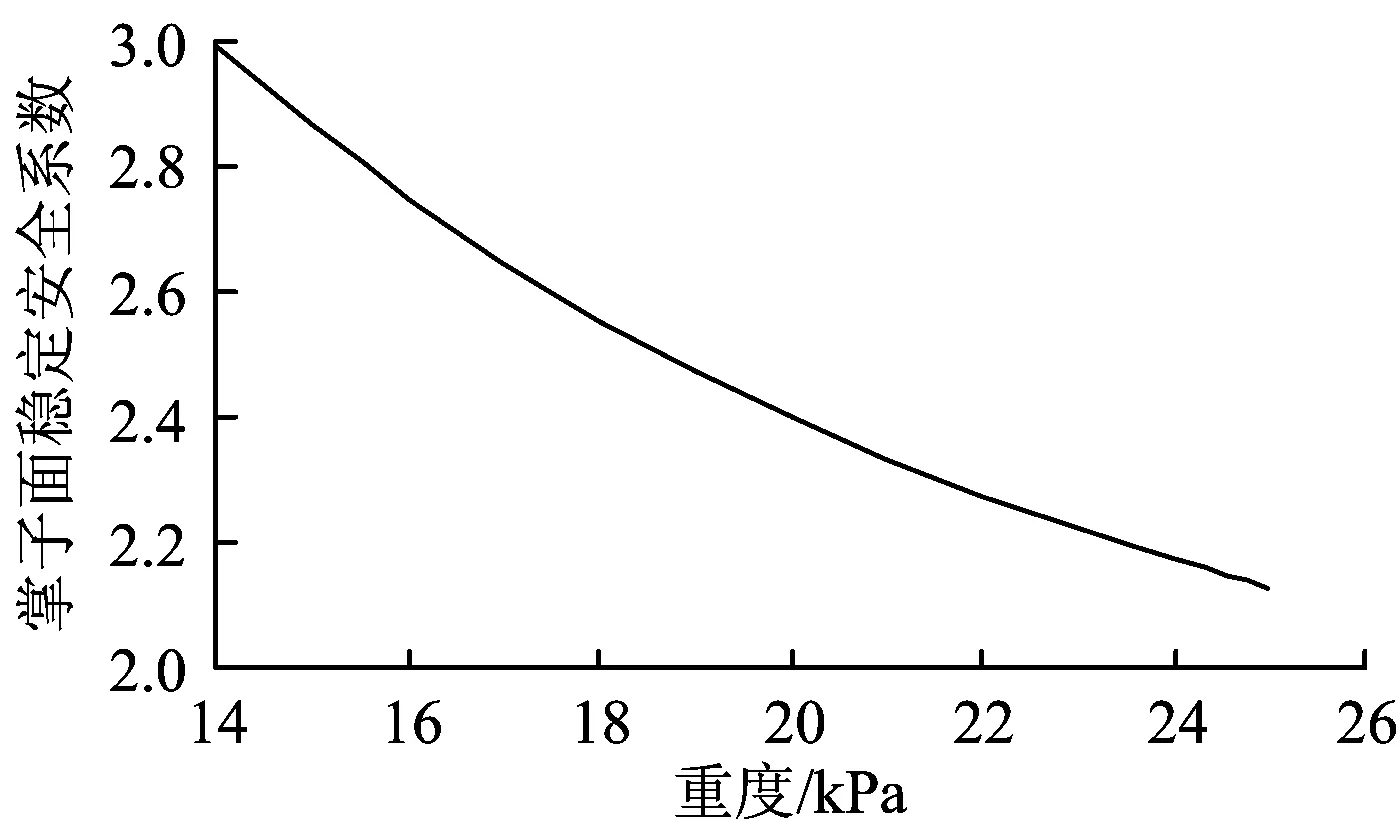
由式(1)可知：a≤0，表示掌子面处于硬的地层中，未涉及软弱地层；0

为了更好地分析掌子面存在软弱地层情况，将掌子面全是硬地层以及全是软地层也进行建模，并做对比，为此，取a=-1.00，0，0.33，0.50，0.67，1.00，2.00进行有限元模拟分析。

2 掌子面稳定性分析方法

为了获得掌子面稳定安全系数和临界失稳塌方形态，首先进行有限元模拟，然后采用强度折减法进行分析。强度折减法原理参见文献[14]，即根据式(2)不断折减抗剪强度参数c和φ，使其达到临界状态，此时的折减系数K即为掌子面稳定安全系数。同时，为了对比有限元模拟结果，采用极限分析法研究掌子面全部处于软弱地层中的稳定情况。

(2)

式中：c′为按K值折减后的黏聚力；c为围岩黏聚力；φ′为按K值折减后的内摩擦角；φ为围岩内摩擦角。

3 有限元模拟结果分析

3.1 掌子面稳定安全系数

图3给出了不同a下的K，从图中可以看出，整体上曲线分为以下3段。

第①段，a≤0，此段K基本没有变化，此时掌子面不存在软弱地层，隧道施工很安全。

第②段，0

第③段，a≥1，掌子面全部处于软弱地层中，且软弱地层已达到中台阶，软弱地层的相对厚度对掌子面的稳定性影响较小。

图3 掌子面稳定安全系数

3.2 掌子面破坏形态

由上述分析可知，只有在掌子面范围内存在上软下硬地层时，上部软弱地层才对掌子面稳定性有影响。因此下面分析掌子面范围内存在上软下硬地层，即a=0.33，0.50，0.67时掌子面的破坏形态。

不同a下掌子面失稳时的位移如图4所示。由图可知：随着a的增加，掌子面前方围岩发生位移的范围增大；当a较小时，位移只发生在上软层的局部，而下硬层的位移较小。

图4 不同a时掌子面失稳时的位移

不同a时掌子面前方塌方体形态如图5所示。由图可知：随着a的增加，掌子面前方塌方体的体积增大，塌方范围扩大，包括塌方体的高度和深度都在增加；塌方体上部形状类似于一个帽子(中间面形状类似抛物线)，下部边界类似于对数螺旋线。

图5 不同a时掌子面前方塌方体形态

不同a时掌子面变形形态如图6所示。由图可知：掌子面上软层的位移要较下硬层的位移大很多，这主要是因为下硬层的变形模量比上软层的变形模量大，在同样荷载作用下，变形模量小的位移要大；另外由于掌子面四周围岩的约束作用，导致掌子面软弱地层中心的位移要较四周的大，呈现一个鼓出的状态，且最大位移发生在掌子面软弱地层厚度的中心偏下位置，如当掌子面全部处于软弱地层中时，最大位移在掌子面中心偏下位置。因此，掌子面中心偏下位置是掌子面位移控制的关键，在施作掌子面正面支护时(如掌子面锚杆)，这个部位应加密加强。

图6 不同a时掌子面变形形态

3.3 地表沉降槽形状

a=0.50时地表沉降云图和沉降槽形状如图7所示，可见，隧道中心对应的地表沉降最大，向四周逐渐减小，形成1个凹坑；a取其他值时情况与此类似。

图7 地表沉降变形云图与沉降槽形状

软弱地层相对厚度系数与掌子面稳定安全系数、地表最大沉降之间的关系见表2。由表2可知：临界塌方时，地表沉降槽的最大沉降和掌子面稳定安全系数均随着a的增大而减小。这是由于对于同样的围岩，a增大，掌子面稳定安全系数降低，即围岩折减得少，发生掌子面塌方时，所以变形才减小。

表2 软弱地层相对厚度系数与掌子面稳定安全系数、地表最大沉降之间的关系

3.4 掌子面临界失稳时应力传递路径

不同a时应力传递路径如图8所示，由图8可得如下结论。

(1)随着a的增加，掌子面前方的应力场发生变化，最大主应力迹线发生偏转，且发生应力偏转的范围扩大，也即开挖的影响范围在扩大。

(2)掌子面上软地层的应力偏转影响范围较下硬地层的更大，表明开挖对上软地层的影响较下硬地层影响大，更易导致上软地层的局部失稳。

(3)当应力发生偏转，形成拱形，即存在拱效应，上部荷载通过应力拱进行传递，此处是掌子面纵向拱效应。随着掌子面软弱地层厚度的增加，应力拱的范围在扩大，且传递到掌子面下部的力更大，因此更应注重掌子面下部的加固，这个也印证了3.2小节中结论，掌子面中心偏下是位移控制的关键。

图8 不同a时应力传递路径

4 掌子面稳定的极限分析

4.1 极限分析掌子面稳定的原理

利用文献[16]求解支护力的公式并结合强度折减法分析上软下硬地层掌子面的稳定性。为了将极限分析的结果应用于矿山法，此处将支护力称为虚拟支护力，对围岩的强度参数进行折减，应用折减后的参数求解掌子面虚拟支护力，当虚拟支护力为0时的折减系数，即为掌子面稳定安全系数。

4.2 虚拟支护力计算公式

掌子面极限分析受力原理如图9所示。图中：掌子面的破坏模式由2个刚性块体 ①及③和1个剪切区 ②构成，块体①是1个顶角为2φ的三角形OO′B；块体③是1个等腰三角形OAE，AE线与水平方向的夹角为β=π/4+φ/2；剪切区②是1个以对数螺旋线BE围成的剪切区OBE，点O为对数螺线中心点，点B和点E分别为对数螺线的起点和终点；σs为地表超载；σt为掌子面虚拟支护力；C为隧道覆土厚度；D为隧道开挖高度；h为O′到工地的距离；la为地表塌陷宽度；va为块体①的速度；vOE为剪切区②在E点的速度；vOB为剪切区②在B点的速度；vC为块体③的速度。

图9 掌子面极限分析受力原理

根据极限分析原理[15]，掌子面虚拟支护力计算公式为

σt=γDNγ+σsNs-cNc

(3)

式中：γ为围岩重度；Nγ，Ns，Nc分别为重度、超载和黏聚力的承载系数， 具体含义参见文献[17]。

4.3 掌子面稳定安全系数

不同折减系数下的掌子面虚拟支护力如图10所示，从图可得如下结论。

(1)当折减系数为2.40时，虚拟支护力为0，也即掌子面稳定安全系数为2.40。

(2)随着折减系数的增大(即围岩性质变差)，掌子面所需要的虚拟支护力呈现非线性增大，且在折减系数小于2.40时，增加的梯度较大，然后增加的梯度较小。

(3)如果曲线从右向左看，随着折减系数的降低(即围岩性质得到改善)，掌子面所需要的虚拟支护力降低，且降低幅度越来越大，表明通过改善围岩性质，如注浆等，可以有效降低掌子面虚拟支护力，提高掌子面的稳定性。

图10 不同折减系数下掌子面虚拟支护力

5 结果对比验证

5.1 掌子面稳定安全系数对比

当a=0.67时，采用本文的有限元强度折减法得到的掌子面稳定安全系数是2.90，而采用极限分析法所得掌子面稳定安全系数为3.42，比有限元强度折减法要大。分析其原因主要有以下两方面。

(1)断面形式的不同，文献[16]应用于盾构隧道圆形开挖面的支护力研究，本文隧道开挖是新奥法施工马蹄形隧道。

(2)极限分析的破坏模式顶部为圆锥形，而有限元模拟的塌方顶部类似于抛物线，两者形状不太一致，破坏模式的不同会导致结果有所差异。

5.2 掌子面破坏形态对比

图11给出了文献[17—19]中掌子面的塌方情况，对比图5与图11可以得出如下结论。

图11 掌子面试验塌方形态

(1)3个文献在上部的破坏模式有些差异。其中，文献[17]的上部类似锥体，且为局部塌方破坏，这与极限分析的结果类似。文献[18]的上部是1个斜向上的圆锥体，也为局部破坏。文献[19]随着覆跨比C/D的不同呈现不同的破坏模式，覆跨比小时为冒顶塌方，覆跨比大时为局部破坏；塌方体顶部像抛物线状，中间部分类似筒状，下部为对数螺旋体。

(2)3个文献掌子面塌方体下部曲线均类似于对数螺旋线，这与本文有限元模拟结果及极限分析结果均一致。

6 参数影响规律

由公式(2)和公式(3)可知，影响掌子面稳定系数的参数主要有围岩的黏聚力c、内摩擦角φ、重度γ、开挖高度D、地表超载σs和覆跨比C/D等，下面分析各参数对掌子面稳定性的影响规律。

6.1 围岩黏聚力对掌子面稳定安全系数的影响

黏聚力对掌子面稳定安全系数的影响曲线如图12所示，可见随着黏聚力的增大，掌子面稳定安全系数提高，当c<10 kPa时，掌子面稳定安全系数小于1。可以认为，围岩性质差或黏聚力小，会使得掌子面稳定安全系数降低，且降低幅度很大。这也是在松散围岩地段易发生塌方的原因(松散围岩的黏聚力很小，无自稳能力或自稳时间很短)。

图12 黏聚力对掌子面稳定性的影响

6.2 围岩内摩擦角对掌子面稳定安全系数的影响

内摩擦角对掌子面稳定安全系数的影响曲线如图13所示，可见随着内摩擦角的增大，掌子面稳定安全系数得到提高，但是提高的幅度不一样。

图13 内摩擦角对掌子面稳定性的影响

对比图12和图13可知，提高围岩黏聚力比提高围岩内摩擦角更能改善掌子面稳定性，也即掌子面稳定性对黏聚力更加敏感。

6.3 黏聚力、内摩擦角对掌子面稳定安全系数的共同影响

掌子面失稳时，围岩弱化表现出黏聚力和内摩擦角均降低，因此很有必要研究黏聚力和内摩擦角共同对掌子面稳定性的影响。

黏聚力和内摩擦角对掌子面稳定安全系数的影响曲线如图14所示，由图可得如下结论。

图14 黏聚力、内摩擦角对掌子面稳定性的共同影响

(1)黏聚力和内摩擦角共同对掌子面稳定安全系数的影响，并不是1个平面，而是1个曲面，表明黏聚力和内摩擦角共同对掌子面稳定性的影响也表现出非线性特性。

(2)图14(a)中，把等值线的拐点用虚线连接起来(图中的虚线)，则其类似于地形图中的山脊线，即此虚线上掌子面稳定安全系数最高，两侧最低，故称此虚线为最优路径。

(3)当黏聚力低于5 kPa时，不论内摩擦角如何大，掌子面稳定安全系数始终小于1，表明弱胶结松散围岩地段更易发生塌方，不能自稳，必须采取加固措施，这个与《公路隧道设计规范》中关于围岩自稳能力的判断相吻合。

6.4 围岩重度对掌子面稳定安全系数的影响

围岩重度对掌子面稳定安全系数的影响曲线如图15所示，可见随着围岩重度的增加，掌子面稳定安全系数降低。

图15 重度对掌子面稳定性的影响

6.5 隧道开挖高度D对掌子面稳定安全系数的影响

开挖高度对掌子面稳定安全系数的影响曲线如图16所示，可见随着开挖高度的增加，掌子面稳定安全系数降低，但是降低的幅度不一样。因此，对于软弱围岩，应采取分部开挖，降低一次开挖的高度。

图16 开挖高度对掌子面稳定性的影响

6.6 覆跨比C/D对掌子面稳定安全系数的影响

覆跨比对掌子面稳定安全系数的影响曲线如图17所示，由图可得如下结论。

(1)当C/D≤0.75时(即覆土厚度C≤3.42 m)，随着C/D的增加，掌子面稳定安全系数降低。

(2)当0.753.42 m)，随着C/D的增加，掌子面稳定安全系数得到提高。

所以，对于超浅埋段，掌子面的稳定性随着覆土厚度的增加而降低。此段最好采用明挖法施工，无条件采用明挖的，宜采用浅埋暗挖法施工，切实做好掌子面的超前支护与加固。

(3)当C/D≥3.00时，掌子面稳定性系数不变。当C/D≥3.00时可以认为隧道是深埋的，此时深埋对掌子面的稳定性不影响，这与图11(c)中深埋的情况类似。

(4)该曲线存在极值，这可以将其作为确定隧道合理埋深的参考条件之一。

图17 C/D对掌子面稳定性的影响

6.7 软弱地层相对厚度系数对掌子面稳定安全系数的影响

软弱地层相对厚度系数a对掌子面稳定安全系数的影响曲线如图18所示，由图可得如下结论。

(1)随着a的增加，掌子面稳定安全系数降低；

(2)从曲线的斜率来看，当a≤0.3时，降低最快；其次是0.3

图18 软弱地层相对厚度系数对掌子面稳定性的影响

6.8 地表超载对掌子面稳定安全系数的影响

2种不同覆跨比时地表超载对掌子面稳定安全系数的影响曲线如图19所示，由图可得如下结论。

(1)当C/D=2.26时，随着地表超载的增大，掌子面稳定安全系数呈线性降低。因此，在掌子面稳定性差且浅埋地段，对地表超载要进行控制，如限速、禁止堆载等。

(2)当C/D=3.00时，随着地表超载的增大，掌子面稳定安全系数不变。这是由于隧道埋深较深，地表超载通过拱效应向两侧传递扩散，不会传递到掌子面。另外，根据Boussinesq公式或Saint.Venant原理，也可知地表超载随着隧道埋深的增加，其影响的程度逐渐降低。

图19 地表超载对掌子面稳定性的影响

7 结 论

(1)软硬地层分界线在拱顶及以上位置，上部软弱地层的厚度不影响掌子面的稳定；此时应关注已支护段安全。软硬地层分界线在掌子面，软弱地层相对厚度系数越大，稳定性越小；掌子面中心上部的软弱地层对稳定性的影响更大。软硬地层分界线在掌子面以下，软弱地层的厚度对掌子面的稳定性影响较小。

(2)随着软弱地层相对厚度系数的增加，掌子面前方塌方体的体积增大，塌方范围扩大，包括塌方体的高度和深度都在增加；塌方体上部形状类似于一个帽子，下部边界类似于对数螺旋线。最大位移值在掌子面软弱地层中心偏下位置，此处是掌子面位移控制的关键。

(3)掌子面应力发生偏转，形成拱形，存在纵向拱效应，上部荷载通过应力拱进行传递；随着软弱地层相对厚度系数的增加，应力拱的范围在扩大，且传递到掌子面下部的力更大，因此更应注重掌子面中心偏下部的加固。

(4)黏聚力较内摩擦角更能影响掌子面稳定性，低黏聚力围岩更易发生塌方；黏聚力和内摩擦角对掌子面稳定性的共同影响存在最优路径。

(5)掌子面稳定性随着重度、开挖高度的增大而增大，随着软弱地层相对厚度系数的增大而减小，曲线梯度均呈现前陡后缓，因此应从降低围岩含水量、减小开挖高度等方面改善掌子面稳定性。覆跨比C/D对掌子面稳定性影响存在极值，此可作为确定隧道合理埋深的参考条件之一。地表超载只在浅埋情况下才影响掌子面的稳定性。