地铁交叉隧道盾构施工的三维有限元分析
□文/周印堂 王达麟
地铁交叉隧道盾构施工的三维有限元分析
□文/周印堂 王达麟
某新建地铁隧道工程近距离垂直上穿既有地铁隧道,采用有限元软件M i das/G TS模拟了新建双线盾构隧道施工对上部地表和下部既有隧道变形的影响。计算结果给出了新建盾构隧道近距离垂直上穿既有双线地铁隧道时的位移变化规律。
交叉隧道;盾构施工;变形;有限元;三维;地铁
随着我国城市化进程的飞速发展,地铁建设项目的数量、规模及对地下空间开发利用的需求不断加大,而受某些特定因素的限制,在同一区域内地铁隧道相互穿越的的情况逐渐增多[1]。其中某些新建隧道与既有隧道交叉段距离较近,对既有隧道安全构成较大的威胁,同时也增加了新建隧道的施工难度[2~3]。大量的地铁隧道工程实践表明,隧道施工势必会引起地层变形[4]。对于交叉隧道来说,新建隧道的开挖是发生在既有隧道施工后的,等于对土体进行了二次扰动,引起复杂的应力重分布,这就对新建隧道提出了更高的设计和施工质量要求[5]。
针对交叉隧道开挖对既有线隧道影响的问题,国内外学者开展的研究较少。之前开展的研究大多是针对平行隧道以及上下重叠隧道,取得了较大成果[6~8]。本文运用Midas/GTS有限元软件,对天津地铁4号线隧道开挖对下部天津地铁3号线交叉区间隧道影响进行三维模拟,模拟隧道开挖过程,研究4号线隧道开挖施工过程中上部地表和下部3号线隧道的力学规律。
1 工程概况
1.1 工程背景
天津地铁4号线盾构区间在CK22+850.0处上穿既有3号线盾构区间结构,隧道顶部距离3号线区间结构竖向净距约1.2 m,两地铁线交角约为87°。新老隧道的外径均为6.2 m,管片厚度均为350 mm。新建4号线隧道左、右线净距10.8 m,交叉段4号线隧道埋深5.1 m。既有地铁3号线隧道左右线净距8.8 m,交叉段3号线隧道埋深12.5 m。交叉段上部地面为大沽北路。3号线与4号线隧道交叉段的位置关系见图1-图2。

图1 隧道结构平面
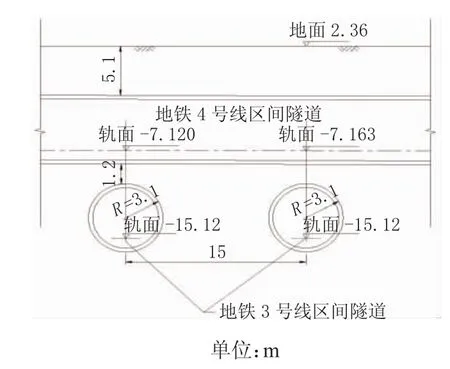
图2 交叉隧道立面关系
1.2 工程地质条件
隧道交叉段所处地层的地质参数见表1。

表1 土体物理力学指标
2 有限元计算模型
采用岩土与隧道领域专用分析软件Midas/GTS,根据工程实际情况,建立有限元计算模型,根据其破裂面的影响范围,沿地铁4号线隧道方向取57 m,沿地铁3号线隧道方向取51 m,上下高度取50 m。模型共51 785个单元。
2.1 本构关系的选择
土体选用Mohr-Coulomb屈服准则,该准则能反映土体的抗压强度不同的S-D效应(Strength Difference Effect)与对静水压力的敏感性,而且简单实用,土体参数c、φ值可以通过各种不同的常规试验测定。因此,较其他准则具有较好的可比性,在工程实践中有着重要的作用和地位,得到了广泛的应用[9]。隧道盾构管片采用板单元模拟。管片采用C50混凝土,其材料物理力学指标见表2。

表2 结构物理力学指标
3.2 计算模型和步骤
有限元计算模型见图3和图4。土体和隧道结构选用四节点三维实体单元,首先建立初始自重应力场,计算模型中第一阶段为开挖的初始阶段,计算出土体在自重的作用下的位移场和应力场,通过Midas/GTS的位移清零功能消除已经完成的沉降位移并构造初始应力场。模型侧面和地面为位移边界,侧面限制水平位移,地面限制竖向位移,上表面取自由边界。
对计算模型进行隧道开挖模拟时,首先对左线隧道进行开挖,然后对右线隧道进行开挖,开挖每完成一步后施加一次隧道管片。土体开挖和管片施作通过钝化和激活单元实现。
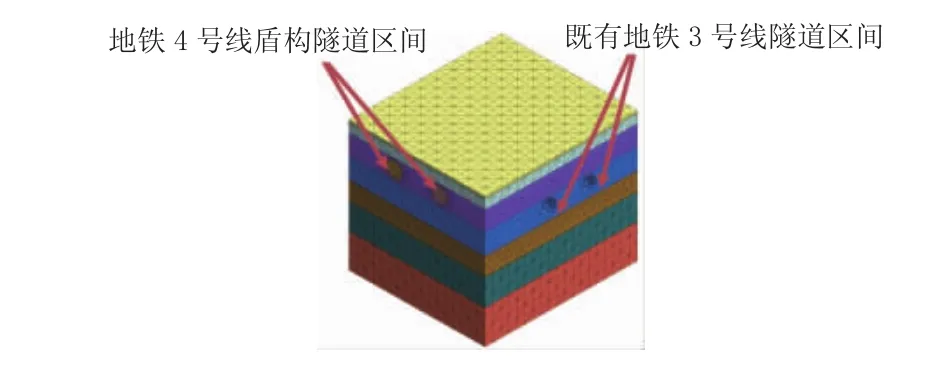
图3 有限元计算模型
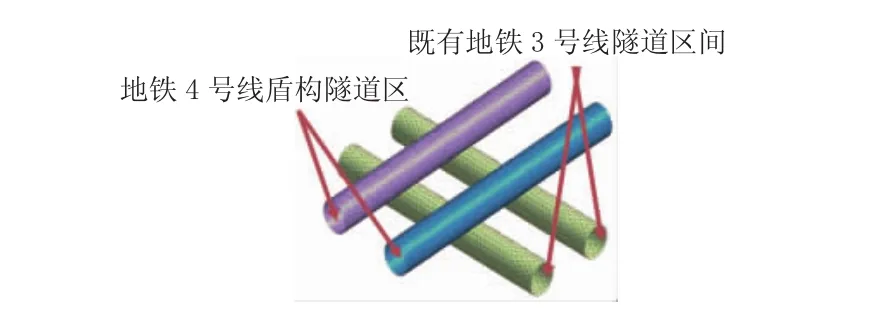
图4 隧道交叉模型
4 计算结果分析
通过对隧道开挖过程的有限元分析,研究地铁4号线隧道开挖施工过程中地表和地铁3号线隧道区间的变形及应力变化,评价地铁3号线的正常运营及结构安全。
4.1 地表土体位移分析
左线和右线隧道开挖完成后,地表土体的位移见图5。从计算结果可以得出,在4号线隧道开挖过程中,地表沿隧道开挖方向发生沉降,形成一个沉降槽。右线开挖完成后的沉降值大于左线开挖完成后的沉降值。左线隧道开挖完成时,位移最大值出现在左线盾构区间大约40 m位置对应的地表部位,最大沉降量为3.18 cm;右线隧道开挖完成时,位移最大值同样出现在右线盾构区间大约40 m位置对应的地表部位,最大位移值为3.41 cm。
图6为左、右线盾构完成后沿既有地铁3号线隧道轴向地表沉降曲线。由图6可以看出,沉降槽呈“W”形,沉降量随着距盾构区间的距离变化而变化,其距离越近,沉降量越大。
图7为左、右线盾构完成后沿盾构方向地表沉降曲线。由图7可以看出,左线和右线盾构完成后,其盾构区间上部地表沉降趋势是一致的,均为在盾构推进前40 m范围内,地表沉降变化较大,盾构推进至40 m断面处时,地表最大沉降分别为3.13 cm(左线)和3.38 cm(右线)。当盾构推进超过40 m时,沉降变化率减小(变化率分别为1.6%和1%),接近平稳。但右线盾构时右线区间上部地表的沉降量比左线盾构时左线区间上部地表的沉降量略大。分析其原因,是因为左线开始盾构时,土体为原状土,之前受扰动较少;而右线开始盾构时,周围土体已经受到左线盾构时的扰动,右线盾构对土体进行二次扰动,故其沉降量略大。

图5 地表竖向位移

图6 左、右线盾构完成后地表竖向位移(沿3号线轴向)

图7 左、右线盾构推进时地表竖向位移(沿4号线轴向)
4.2 既有3号线位移分析
4号线左线和右线隧道开挖后时,既有3号线管片竖向位移见图8。从计算结果可以看出,由于上部4号线的盾构开挖,引起土体卸荷,导致3号线左右线整体出现上浮。4号线左线盾构完成时,3号线最大的上浮量为3.52 mm,位置在3号线与4号线左线交叉部位3号线管片上部;4号线右线盾构完成时,3号线最大上浮量为3.96 mm,位置在3号线与4号线右线交叉部位3号线管片上部。

图8 既有3号线竖向位移
图9为4号线左线盾构推进时3号线左右线顶部的竖向位移变化曲线。由图9可以看出,3号线左线的最大上浮量为3.63 mm,发生在4号线盾构推进到大约30 m附近位置,此时掌子面位于3号线左线与4号线左线的交叉位置。而3号线右线的最大上浮量为3.543 mm,发生在4号线盾构推进到大约45 m附近位置,此时掌子面位于3号线右线与4号线左线的交叉位置。
对于其影响范围,对于3号线左线,在盾构推进前15 m范围内,3号线左线的竖向位移很小,均<0.1 mm;在掌子面过了15 m位置之后,3号线左线的上浮量开始呈线性增长,直到30 m附近位置上浮量达到最大,然后在40 m位置稍微衰减,最后保持平衡。当4号线左线掌子面距3号线左线中线大约为8~13 m时开始对3号线左线的变形真正产生影响。同理,对于3号线右线,在盾构推进前30 m范围内,3号线右线的竖向位移很小;在掌子面过了30 m位置之后,3号线右线的上浮量开始呈线性增长,直到45 m附近位置上浮量达到最大,然后开始衰减并保持平衡。可以看出4号线左线盾构施工对3号线左、右线的影响范围是一致的。由此可判断,当4号线左线掌子面与3号线左、右线中线相距≤8~13 m(约1.5~2倍洞径)时,3号线的上浮量开始呈线性增长,可以视为4号线施工对既有3号线开始产生真正的影响。
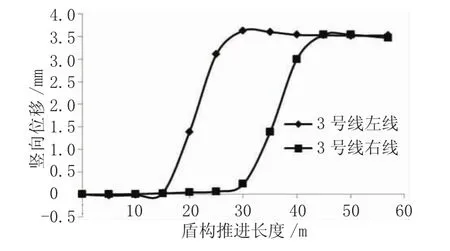
图9 4号线左线盾构推进时3号线左、右线顶部竖向位移变化曲线
图10为4号线右线盾构推进时3号线左右线顶部的竖向位移变化曲线。由图10可以看出,3号线左、右线的最大上浮量分别为3.98、3.83 mm,较左线开挖时左、右线的最大上浮量分别增长了9.6%、8.1%。3号线左线的最大上浮量出现在盾构推进到30 m附近位置,3号线右线的最大上浮量出现在盾构推进到45 m附近位置且左、右线竖向位移的变化趋势与左线推进时的变化趋势较为一致,进一步印证了前述相关结论。

图10 4号线右线盾构推进时3号线左、右线顶部竖向位移变化曲线
5 结论
1)新建地铁4号线隧道推进时会造成上部地表出现沿隧道盾构方向向周围扩散的沉降槽且左、右线均开挖完之后右线上部地表的沉降大于左线上部地表的沉降。
2)新建地铁4号线隧道推进时会造成下部既有地铁3号线结构出现上浮,当掌子面位于与既有隧道(包括左线和右线)交叉部位时,既有隧道的上浮量达到最大。
3)近距离交叉隧道开挖存在空间效应。随着新建隧道的盾构开挖,其对既有隧道的影响由小变大,当4号线盾构施工掌子面与既有3号线左、右线交叉点水平距离≤1.5~2倍洞径时,3号线的位移开始呈线性增长。建议当盾构隧道掌子面距离交叉点3倍洞径时,做好既有线隧道的监控量测工作。
[1]赵乐之,乔 磊.新建隧道与既有隧道交叉段施工方案研究[J].建筑结构,2012,(S1):896-898.
[2]刘辉喜,刘明高,黄始南,等.交叉隧道近接施工安全的数值分析研究[J].中外公路,2011,31(3):221-224.
[3]刘洪洲,孙 钧,蒋树屏.交叠隧道盾构法施工引起地面沉降三维数值模拟[A].海峡两岸岩土工程/地工技术交流研讨会[C].2002.
[4]包德勇.近距离交叠隧道施工影响的数值模拟[J].地下空间与工程学报,2011,7(1):127-132.
[5]何 川,苏宗贤,曾东洋.盾构隧道施工对已建平行隧道变形和附加内力的影响研究[J].岩石力学与工程学报,2007,(10):2063-2069.
[6]Soliman E,Duddeck H,Aherns H.Two and three-dimensional analysis of closely spaced doubled-tube tunnels[J]. Tunnelling and Underground Space Technology,1993,8(1):13-18.
[7]曾小清,张庆贺,曹志远.地铁工程双线盾构平行推进的相互作用[J].同济大学学报,1997,25(4):386-389.
[8]陈先国,高 波.重叠隧道的施工力学研究[J].岩石力学与工程学报,2003,22(4):606-610.
[9]张学言,闫澍旺.岩土塑性力学基础[M].天津:天津大学出版社,2004.
□王达麟/铁道第三勘察设计院集团有限公司。
U452
C
1008-3197(2015)06-44-04
10.3969/j.issn.1008-3197.2015.06.015
2015-04-07
周印堂/男,1975年出生,高级工程师,天津市地下铁道集团有限公司,从事工程技术管理工作。

