染料拼色反射光谱的Bezier曲线建模方法
王波, 金福江, 周丽春
(1. 华侨大学 信息科学与工程学院, 福建 厦门 361021;2. 华侨大学 机电及自动化学院, 福建 厦门 361021)
在纺织印染中,由于光谱与染料质量分数之间的非线性关系,难以得到具有泛用性的光谱建模方法,故无法建立光谱反射率与染料质量分数之间的直接关系,从而发展出三刺激值配色法.现有的计算机测配色系统大多是基于三刺激值配色法,其基础是测量一定光源下的物体色的三刺激值,而三刺激值相等的两个颜色可达到等色效果[1-3].在三刺激值配色法中,Kubelka-Munk理论建立了染料质量分数与三刺激值之间的关系[4],由三刺激值误差进行迭代调整,可得到低异谱性的匹配结果[5].然而,三刺激值无法完全表达某种颜色的全部特性,当观察条件发生变化时,等色可能会被破坏而产生色差.全光谱配色[6]需尽力匹配标准色的光谱曲线,使不同波长下的反射率相同.因此,标准色的表达更加全面,匹配结果更加准确,即使观察环境发生变化,再配色与标准色依然相同[7].
颜色变化为非线性关系,具体表现为不同颜色的光谱特性不同.文献[8-12]对光谱建模进行研究,这些方法虽然能够很好地描述光谱曲线的局部特征,但无法表达光谱曲线的整体特征,造成颜色匹配结果的异谱性.文献[13-15]对光谱与染料质量分数之间的关系进行研究,但这些方法均只适用于某一类颜色的配色方案,局限性较大,没有建立光谱与染料质量分数之间的直接关系.基于此,本文提出一种染料拼色反射光谱的Bezier曲线建模方法[16-17].
1 单一染料染色的反射光谱Bezier曲线模型
定义1用波长为λ的照明光源入射已染色后的干燥、平整、色泽均匀的织物,当染色染料质量分数(w)和照明光源波长变化时,反射光谱率R=f(w,λ)是个曲面函数;当染料的质量分数固定(w为常数),照明光源波长变化时,反射光谱率R=f(λ)为一条反射光谱曲线.
例如,活性红3BS的质量分数从0.01%增加到2.00%,由Datacolor测色系统可得染色后布匹的反射光谱曲线,如图1所示.
定理1通过n阶Bezier函数拟合反射光谱曲线,如图2所示.图2中:折线为Bezier曲线控制多边形,其折点为Bezier曲线控制点;实线为Bezier曲线;虚线为反射光谱曲线.反射光谱的参数方程为
(1)

由式(1)可知:反射光谱的参数方程是由控制点决定,由反射光谱图的数据点求出控制点是反射光谱建模的关键.

(a) 拟合曲线 (b) 调整控制点 图1 染色后布匹的反射光谱曲线 图2 Bezier函数拟合的反射光谱曲线 Fig.1 Reflectance spectrum curve of dyed cloth Fig.2 Reflectance spectrum curve fitted by Bezier function

(2)
采用积累弦长参数化方法[18-19],为每一个光谱坐标点指定一个参数t,以t0为起点,t0=0,tn为终点,tn=1,有
(3)
式(3)中:ti为坐标点Pi(λi,Ri)对应的参数;ΔPi-1为Pi-1与Pi之间的欧式距离;s为顺序两坐标点的距离总和.
得到坐标点及其对应的参数后,可求解出n个控制点(R0,λ0),(R1,λ1),…,(Rn,λn).
定理3单一染料染色的反射光谱Bezier曲线模型可用多项式表示.
用不同质量分数的染料染色,得到染色后织物的反射光谱Bezier曲线.对每条反射光谱曲线拟合的Bezier曲线控制点个数相同,取10个控制点,分析Bezier曲线控制点与单一染料质量分数的关系(图3)可知:单一染料质量分数变化时,反射光谱Bezier曲线控制点纵坐标随质量分数呈对数形式增长(图3(a)),而控制点横坐标变化幅度相对较小(图3(b))

(a) 控制点纵坐标 (b) 控制点横坐标 图3 染色后布匹的反射光谱Bezier曲线控制点的变化曲线Fig.3 Change curve of Bezier curve control point of reflectance spectrum of dyed cloth
对染料质量分数进行线性化处理,则控制点与染料质量分数的关系可以表示为
(4)

对于每一个控制点,由小样实验可得染料质量分数与控制点数据(w,P(j)),再通过最小二乘法计算出控制点关于染料质量分数的表达式的系数矩阵Aj.
单一染料染色时,质量分数为0.01%~2.00%的单一染料染色布匹,均可根据式(4)计算出染色后布匹的反射光谱Bezier曲线的控制点.
令C(w)=[1,w,…,wm]T,则单一染料染色反射光谱Bezier曲线控制点与染料质量分数的关系模型为
P(j)=AjC(w).
(5)
式(5)模型可确定质量分数为0.01%~2.00%的单一染料染色后布匹的反射光谱Bezier曲线.
2 染料拼色的反射光谱Bezier曲线模型
质量分数为0.1%的单一活性染料活性黄3BS、活性红3RS、藏青G分别染色后的布匹反射光谱率,以及3种单一染料拼色染色后的布匹反射光谱曲线,如图4所示.
通过单一染色反射光谱和拼色染色反射光谱之间的关系,分析拼色染色布匹反射光谱与混合染料各组分质量分数之间的关系.通过正交试验方法,得到拼色染色及其对应的单一染料染色结果,控制点P0(λ1,R1),P1(λ1,w1,R1,w1),P2(λ1,w2,R1,w2),P3(λ1,w3,R1,w3)分别由拟合拼色染色和对应的单一染色后布匹的反射光谱曲线得到.拼色染色与单一染色控制点对应表,如表1所示.
定义2染料拼色.拼色是指用多种不同质量分数的单一染料混合均匀进行染色. 因此, 拼色后织物的反射光谱模型为
R=f(w1,w2,…,wm,λ).
(6)

(a) 单一染色 (b) 拼色染色图4 染色后布匹反射光谱曲线Fig.4 Reflectance spectrum curve of dyed cloth
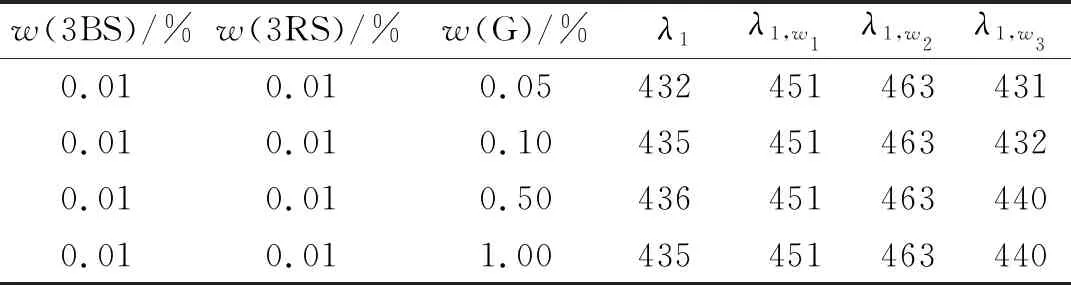
表1 拼色染色与单一染色控制点对应表Tab.1 Corresponding table of control points for color matching and single dyeing
式(6)中:w1,w2,…,wm为m种不同染料的质量分数.
定理4拼色的反射光谱曲线率R=f(λ)可由m种单一染料反射光谱曲线率Ri=fi(λ),i=1,…,m得到.当m种染料质量分数和照明光源的波长都变化时,m种染料拼色的反射光谱模型是一个m+1维超曲面; 当m种染料的质量分数固定时,w1,w2,…,wm为常数,m种染料拼色的反射光谱率为R=f(λ).拼色反射光谱是由固定质量分数的单一染料染色混合得到,因此,拼色的反射光谱率R=f(λ)也可以由m种单一染料反射光谱率Ri=fi(λ),i=1,…,m得到.
定理5当m种染料质量分数变化时,拼色染色后布匹的反射光谱模型可以表示为m个质量分数为wi的单一染料染色光谱模型Ri(wi,λ),i=1,…,m组合,即
R=f(w1,…,wm,λ)=f(R1(w1,λ),…,Rm(wm,λ)).
(7)
定理6拼色染色与单一染料染色后布匹的Bezier反射光谱曲线控制点之间的关系为
P0(w1,w2,w3)=f(P1(w1),P2(w2),P3(w3)).
(8)
式(8)中:P0为拼色染色Bezier反射光谱曲线控制点.
这样可将单一染色与拼色染色的反射光谱曲线关系转化为控制点之间的关系.得到单一染色控制点与拼色染色控制点的模型后,用Bezier方法进行叠加,可得拼色反射光谱Bezier曲线与染料质量分数之间的关系.
定理7对于采用相同Bernstein基函数的单一染料染色光谱Bezier曲线和m个质量分数为wi的单一染料拼色反射光谱Bezier曲线有以下线性叠加关系,即
P0=r1P1+…+rmPm.
(9)
结合单一染料染色Bezier反射光谱曲线模型,拼色染色Bezier反射光谱曲线控制点P0与单一染料质量分数w1~w3的关系可表示为
(10)

(11)
3 拼色染色反射光谱Bezier曲线的色差模型
国际照明委员会(CIE)标准色度系统下的三刺激值X,Y,Z的计算公式分别为

(12)
因此,由拼色染色反射光谱Bezier曲线可以得到任意波长下的光谱R(λ),由式(12)可计算出拼色染色的三刺激值X,Y,Z.

(13)

(14)
反射光谱Bezier曲线控制点已确定,根据定理1,可将式(14)转换成关于参数t的Bernstein基函数的积分形式,从而精确计算出染色织物色泽的三刺激值.
亨特色差ΔEHunter表达式、亨特颜色空间明度指数L和色品坐标a,b的计算公式分别为
ΔEHunter=[(ΔL)2+(Δa)2+(Δb)2]1/2,
(15)
(16)
取标准照明体D65和CIE 1964(10°)观察者,在相同波长下,将拼色染色后的实测反射光谱曲线和用单一染料Bezier曲线叠加的拼色Bezier曲线的三刺激值分别代入式(16).经计算,可得明度指数L及色品坐标a,b的差值ΔL,Δa,Δb;再由式(15)计算出拼色染色后的实测与预测的色差,从而验证多种染料拼色染色后布匹的反射光谱Bezier曲线的准确性.
4 实验与验证
4.1 小样实验
小样实验1为单一染料染色;小样实验2,3为拼色染料染色.小样实验1~3中的浴比均为1∶10,布的质量均为5 g.小样实验1~3的染色配方,如表2,3所示.

表2 小样实验1的染色配方Tab.2 Dyeing recipe of sample experiment 1
织物为双面汗布;染料为3BS,3RS,G;实验采用CADSMG108/00型染液滴定机、HS-24型高温染色小样机、HH-S型恒温水浴机、烘干机、DataColor800型测色配色仪.
用滴液滴定机加染料于染杯,放入布样;将染杯置于60 ℃小样机中45 min;于100 ℃恒温水浴机皂洗5 min;取出样布,进行清洗、烘干;使用测色配色仪测量布匹的反射光谱.
单一染料染色后的反射光谱曲线(小样实验1),如图5所示.图5中:虚线为测得的实际反射光谱率;实线为预测的反射光谱率.

(a) 3BS (b) 3RS图5 单一染料染色的反射光谱曲线(小样实验1)Fig.5 Reflectance spectrum curve of single dye (sample experiment 1)
小样实验2,3先进行不同染料的单一染色,分别测得单一染色的反射光谱曲线,如图6所示;然后,进行拼色染色实验,测得拼色染色的反射光谱曲线,如图7所示.图6,7中:虚线为测得的实际反射光谱率;实线为预测的反射光谱率.

(a) 小样实验2 (b) 小样实验3图6 单一染料染色的反射光谱曲线(小样实验2,3)Fig.6 Reflectance spectrum curve of single dye (sample experiments 2, 3)

(a) 小样实验2 (b) 小样实验3图7 拼色染色的反射光谱曲线(小样实验2,3)Fig.7 Reflection spectrum curve of color matching (sample experiments 2, 3)
4.2 实验分析
分析实际染色后布匹的反射光谱和预测得到的反射光谱,分别计算三刺激值、亨特色差(ΔEHunter),均方根误差(ΔERMS)及光谱匹配精度(GFC),结果如表4,5所示.表4,5中:(Xr,Yr,Zr)为染色布匹的实际三刺激值;(Xp,Yp,Zp)为染色布匹的预测三刺激值;小样实验1取单一染色中色差最大者.

表5 小样实验光谱曲线对比Tab.5 Comparison of spectral curves of sample experiments
由表4,5可知:预测的反射光谱与实际染色的反射光谱的CIE色差均小于4,属于工业染色可接受的范围,证明文中方法的有效性;预测与实际的反射光谱的均方根误差极小;预测与实际的反射光谱匹配精度高,证明文中方法的准确性.
5 结束语
使用Bezier参数曲线表示反射光谱率,可以将染料质量分数与曲线的关系转化为染料质量分数与点的关系,易于光谱重构和匹配.同时,将反射光谱曲线先分段再拟合,使反射光谱曲线的数学表示更加准确.通过分析染料质量分数和反射光谱的关系,建立由单一染料合成拼色染料的函数模型,可直接由染料配方的质量分数计算出染色后布匹的反射光谱率,并由该反射光谱率计算与目标色之间的色差.由染色配方直接预测配色结果和色差,相较于三刺激值配色法的反复迭代和调整过程,文中方法具有快速性和简洁性,且使用反射光谱曲线考察目标色与匹配色,更加准确、真实.

