探讨某连续刚构桥梁合理成桥状态预应力配束技术

何良忠

（贵州桥梁建设集团有限责任公司,贵州 贵阳 550001）

0 引言

桥梁成桥的内力状态分析，通常可划分为成桥和施工阶段的受力状态，其合理的内力状态可划分为三个阶段[1]：第一步是对其进行受力分析，确定其分布特征；其次，进行结构优化，在成桥后，可以根据构件的内力进行调整，以获得最优的应力状态[2]。最后，对成桥后的内力进行模拟，由模拟受力找出偏差控制关键点，调整相应的误差，确保其合理的布置。

1 连续刚构桥的合理成桥状态

预应力平衡设计法的关键在于：将预应力用于平衡构件的自重，加上局部活载所造成的结构应力，使得在给定的载荷组合下，受弯构件仅产生压应力，而不会发生弯曲应力，这样就避免了复杂的混凝土徐变计算[3]。大致的思路用下式表达：

预应力等效荷载←平衡→恒载+k·活载 （1）

式中，k——活载荷的平衡因子，0＜k＜1。根据荷载平衡的原则，利用预应力所产生的力，来抵消其他荷载所引起的应力，从而有效地抑制跨中截面的长期下挠。

为了实现成桥的目的，使桥的长期形变成为目标，必须抵抗活载、温度等因素的不利影响，从而控制桥梁在长期荷载下的变形。

1.1 合理受弯状态

成桥后，在合理的受弯条件下，箱梁的基部应该承受正弯矩，从而平衡活载、温度以及其他荷载对基底产生的负弯矩。跨中应受负弯矩作用，以减少活载、温度和其他载荷对跨中的影响[4]。以三跨连续刚构桥为例，成桥后梁体的中段为负弯矩，而根段截面为正弯矩。反之，则是不合理的弯曲受力。合理受弯状态如图1所示。

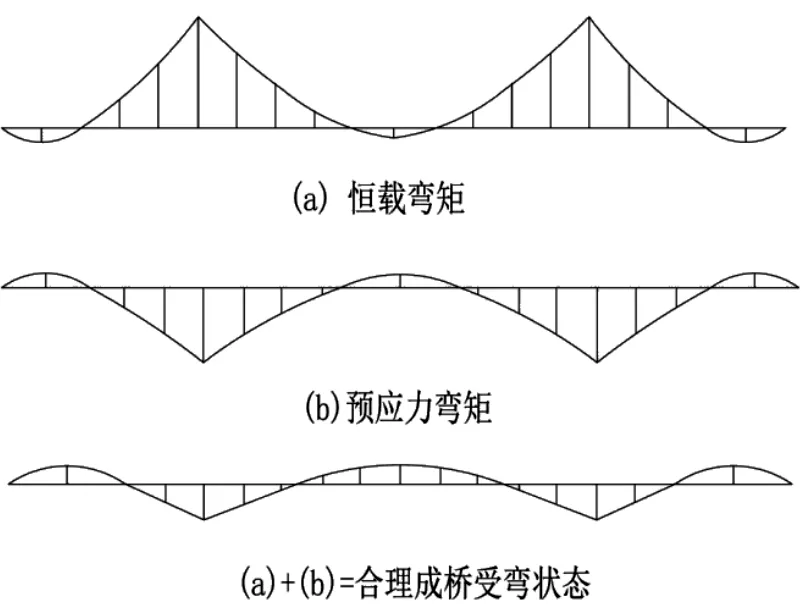
图1 合理受弯状态

1.2 合理受剪状态

在合理的受剪力条件下，成桥预应力引起的剪力，应该与活荷载所造成的剪力的负值相等，从而能够抵消活荷载与其他荷载作用在桥梁上所造成的剪力。当剩余剪力与活荷载作用下的剪力类似时，这是不合理的剪切状态。合理受剪状态如图2所示。

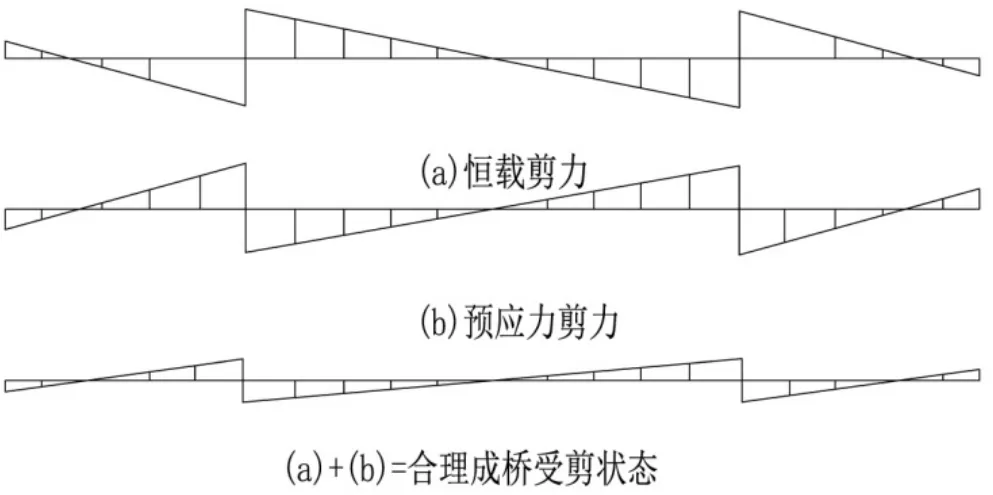
图2 合理受剪状态

剪力对箱形梁的截面位移有一定的影响，但其变化幅度比弯矩的作用要小得多。其重点在于使预应力能抵消恒载作用效应，从而使后期剪力的负面影响降到最低。

1.3 合理的应力状态

成桥的合理应力要求箱梁整体受压，箱梁根部的顶部压应力要比底部的压应力大，而跨中截面底部压应力要大于顶部压应力，这种合理的受力状况能使其在承受外载荷时不会产生拉应力。

以三跨连续刚构桥为例，成桥后的中段底板的压应力比顶板的压应力要大，而且在整个使用期间，底板的压应力始终比顶板的压力大。该应力条件既能平衡跨中的活荷载作用，又能防止因混凝土徐变而引起的跨中过度下挠病害。

2 合龙束次应力效应分析

在主梁的根截面上采用预应力配束，主要实现平衡恒载弯矩的作用。在中跨中段截面上采用预应力配束，主要是用来平衡恒载和活荷载联合作用下的弯矩[5]。为了充分利用预应力钢筋束的最大效能，通常将其设置在顶板或底板上，以增加其偏心弯矩。

为了对跨中底板合拢束所引起的次弯矩进行量化，明确其对总弯矩影响的大小，需定义跨中底板合拢束的预应力效率系数：

式中，β——预应力的效率系数；M0——预应力初始弯矩；Ms——预应力的次弯矩。以等截面的三跨连续梁为例，如图3，通过计算，可得跨中底板束次弯矩公式：

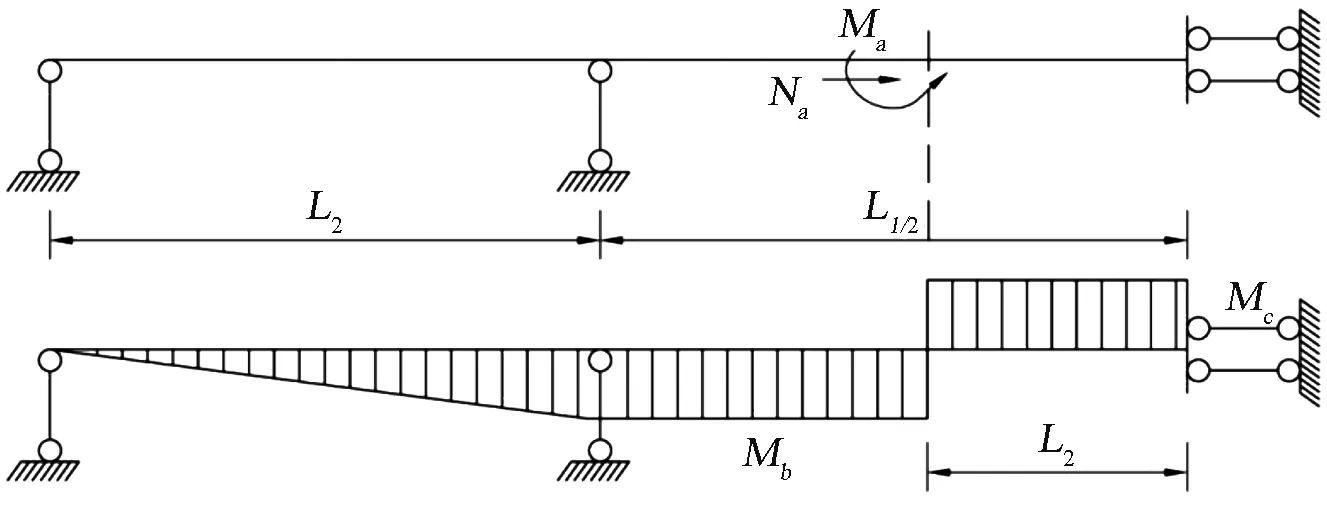
图3 求解等截面梁跨中合龙束次弯矩的计算简图

式中：L1——中跨的长度；L2——边跨的长度。

因此，三跨等截面连续梁的预应力效率系数公式如下：

从以上结果可以看出，跨中底板束所产生的次弯矩与其设计长度Lm、初始弯矩M0相关。底板束段的设计长度愈大，所产生的次弯矩Ms愈大，底板束流效能系数η愈小。变截面连续刚构桥，由于箱梁在不同部位的断面是不断变化的，因此不能用等截面梁法进行跨中预应力次弯矩的计算。但由式（3）来判定变截面梁的预应力次弯矩的变化，或通过对上述式的系数进行修正，得出跨中次弯矩的近似公式：

因此，在变截面梁跨中，底板束的预应力效率系数为：

式中，ξ——变截面梁的弯矩校正系数；η′——预应力效率系数。

变截面梁的预应力效率系数η′的大小与梁底的抛物线形状有关，在同一跨度刚构桥中，梁底的抛物线形状对其预应力系数的作用随抛物线数的增加而增加；在不同跨径、跨距较小的情况下，抛物线的改变对结构的预应力效率系数影响较小[6]。在大跨度的梁底部，抛物线形状的改变，对结构的预应力效率有很大的影响。研究结果表明，当跨径减小，跨中底板的合拢束的作用也随之提高。

见图4，某三跨预应力混凝土连续刚构桥，假定三个预应力钢筋束在桥身的中间底板上，从长到短记为l、m、s。考虑了初始和次弯矩的影响，结果表明：随着预应力钢筋束长度的增加，跨中截面的总扭矩减小，预应力效率降低；长短束在整个桥梁中所产生的预应力总扭矩是不一样的，长束的负弯矩覆盖区间要大于短束，在根部截面引起的正弯矩要大些，而短束的负弯矩覆盖区间要小，在根部截面引起的正弯矩要小些。

图4 不同长度合龙束的总弯矩

但换个角度来看，在梁根部截面的底板合拢束次弯矩为正弯矩，能减小根部截面的受力。主梁根部的负弯矩的减小值是：

式中，Mreduce——跨中截面根部合龙束的次弯矩。

3 预应力筋的定量设计方法

通过对成桥结构的分析，确定了截面预应力的设计弯矩，并推导出了梁体跨中和根部截面的预应力钢筋用量的计算公式。悬臂梁根部预应力束数量：

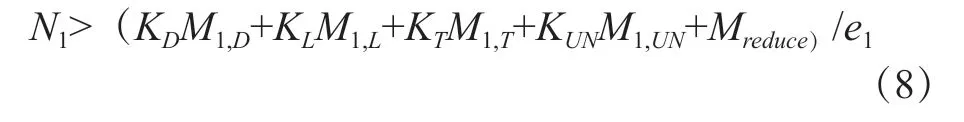
式中，N1——根截面上施加的有效预加力；M1,D——由恒载引起的根截面上的弯矩；M1,L——根截面上的活荷载所引起的弯矩；M1,T——根部截面上，温度效应引起的弯矩；M1,UN——根截面上的其他载荷所引起的弯矩；e1——根截面的预应力偏心率。

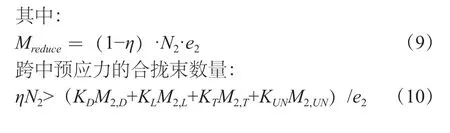
式中，N2——跨中截面有效预应力；M2,D——在恒载作用下，跨中截面上的弯矩；M2,L——跨中截面上的活荷载所引起的弯矩；M2,T——跨中截面的温度所引起的弯矩；M2,UN——由其他荷载引起的跨中截面的弯矩；e2——跨中截面的预应力引起的偏心距；η——跨中合拢束的效率系数，在计算边跨底板合拢时，应考虑中跨合拢造成的边跨弯矩增大，见公式（11）：

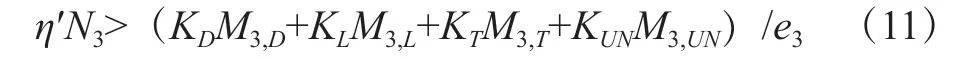
式中，N3——边跨梁的有效预应力；M3,D——恒载时，边跨梁截面上的弯矩；M3,L——边跨梁上的活荷载作用，产生的弯矩；M3,T——边跨梁截面的温度引起的弯矩；M3,UN——其他荷载作用于边跨梁截面所产生的弯矩；e3——边跨梁截面的预应力偏心距；η′——计算边跨梁合龙束的效率系数。

4 算例对比

4.1 项目概况

某桥梁是一座宽9 m，跨径为（110+235+110）m的连续钢构桥，公路等级：二级公路，设计速度为每小时40 km。桥面采用8 cm厚的现浇层+防水+9 cm厚的沥青混凝土，上部结构采用吊篮分段现浇，桥型布局如图5。

图5 大桥桥型布置图

为直观地反映出合理成桥条件下，连续刚构桥配束方法与原有设计的不同，按照公式（11）及计算出的合理成桥弯矩，分别以跨中截面与中跨根部截面的钢绞线数进行比较，弯矩取其截面最大值和最小值，再进行平均，计算结论如表1。

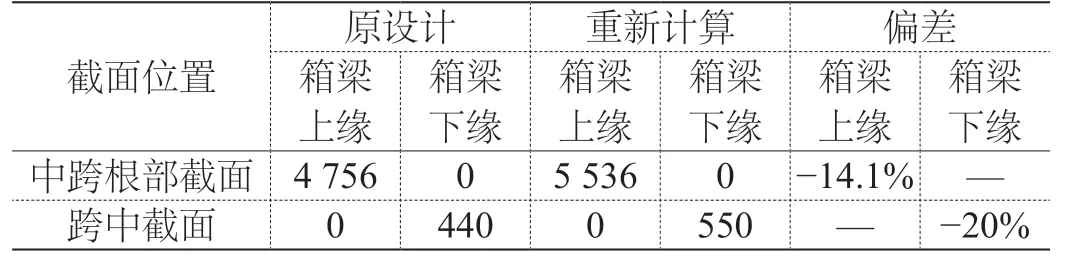
表1 根部与跨中截面钢绞线数量对比

由表1可知，在成桥条件下，中跨根部和跨中的截面，预应力配束量要大于设计值。这尽管在一定程度上提高了大桥的成本，但是其长期安全性、耐用性，却是非常有意义的。

4.2 与原设计成桥弯矩对比

在成桥条件下，按合理的弯矩平衡公式，求出成桥条件下的弯矩可行区域，并以其中间值为先期计算的弯矩初值[7]。然后，根据其极限承载力与正常使用极限状态的要求，对其进行截面应力校核，但最后的预应力布置，必须在合理的区域之内。通过Midas/civil查询原始成桥弯矩，比较了由成桥条件下的弯矩平衡公式得出的成桥弯矩，结果表明：根据成桥原理计算出的成桥弯矩与原来设计的成桥弯矩相比，在受力上更为合理，见图6。

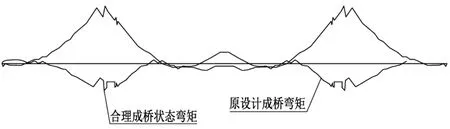
图6 合理成桥状态弯矩与原设计成桥弯矩

在成桥条件下，梁体的根部应为正弯矩，使其在成桥后能够抵御因活载、温度等因素而引起的负弯矩；跨中部位为负弯矩，能有效地抵御因活载、温度等可变载荷作用而产生的负面影响[8]。

5 结论

预应力钢束的设计，要考虑的主要因素包括：主梁截面构造、钢束布置位置、钢束布置长度、钢束锚固位置和钢束张拉形式等因素。这些因素决定了预应力钢束在按合理的成桥弯矩布置后，需要对其极限承载力、极限工况和截面应力校核等进行反复试算和修正，从而得出预应力配束组合的最终方案。因此，文中所述的预应力钢束的设计只是一个初步的定量分析，还需要进一步计算和调整。从成桥角度来看，在合理的成桥条件下形成的弯矩具有更大的优越性。