一种考虑初始弯矩的箱型梁水下爆炸试验方法

郑 监, 卢芳云, 李翔宇, 梁 文, 陈 荣

一种考虑初始弯矩的箱型梁水下爆炸试验方法

郑 监, 卢芳云, 李翔宇, 梁 文, 陈 荣

(国防科技大学 文理学院, 湖南 长沙, 410073)

箱型梁是船舶缩比水下爆炸试验中的常用模型, 但由于材料规格和焊接工艺的限制, 所采用的箱型梁板厚都比按完全缩比的大。过大的板厚使箱型梁具有更大的抗弯刚度, 因此, 采用此类模型进行水下爆炸试验时会低估水下爆炸的威力, 使试验结果很难直观地映射到实际模型。为了抵消过大刚度带来的影响, 文中引入初始弯矩的思路, 建立了一种能实现弯矩幅值和分布可控的箱型梁水下爆炸试验方法。通过试验结果对比发现, 文中所介绍的考虑初始弯矩的箱型梁水下爆炸试验方法能降低模型板厚带来的影响, 可为船舶缩比水下爆炸试验的设计提供参考。

水下爆炸试验; 弯矩; 箱型梁

0 引言

提高船舶的抗爆抗冲击性能是保证船舶生命力的一项重要前提。进行实船爆炸试验是评估船舶抗爆抗冲击性能最准确有效的方式, 但需要耗费大量资金, 且实施较为困难。因此, 一般采用实尺寸模拟[1-2]或缩比模型相似试验[3-4]进行替代。在缩比模型相似试验方面, 如果缩尺比较大, 耗费依旧很大, 意义不大; 如果缩尺比较小, 则对模型的制造工艺提出了更高要求, 例如要保证完全几何相似, 则需要极薄的钢板和很高的焊接技术。为了回避这一技术难点, 很多小缩尺比的模型试验[5-8]一般不保证完全几何相似, 即船的长、宽、深等大型几何尺寸保证相同的缩比尺, 但板厚等小型几何尺寸不保证相似, 一般而言, 实际缩比模型的厚度都比完全几何相似模型的厚度厚。过大的板厚使得不完全几何相似模型的抗弯刚度比完全几何相似模型大, 相关试验结果对揭示毁伤机理提供了很多有价值的结论, 但如果基于此类试验结果直接预测实际情形会低估水下爆炸的威力。

为了使这种不完全几何相似模型的试验结果能用于实船的评估和考核, 有学者进行了相似理论的研究[9-11], 也有学者提出了畸变模型的方法[12-14]。该方法通过大量数值仿真, 构建出不完全几何相似模型(畸变模型)与完全几何相似模型之间的各个物理量(速度、周期等)与畸变参量之间的函数关系, 然后通过畸变模型的试验结果反推得到完全相似模型的结果, 进而得到原模型的结果。畸变模型方法的难点在于畸变参量缩比尺度的确定,以及需要进行大量数值仿真和误差分析; 而其通过数值仿真数据建立的函数关系可靠性仍需要进行更多试验验证。

如果忽略应变率效应的影响, 当炸药尺寸、爆炸距离和结构的所有尺寸都满足相同缩尺比时,结构表面的冲击波压力和结构内的应力相同。如果令模型(model)与模型(prototype)的特征长度缩比尺为λl=Lm/Lp, 则完全几何相似模型的截面惯性矩缩尺比λI=λl4, 而不完全几何相似模型的截面惯性矩由于厚度较大, 其缩尺比要比完全缩比结构的截面惯性矩大, 即。

作用在箱型梁上的弯矩主要受长度尺寸影响,不论是完全几何相似模型还是不完全几何相似模型, 其力矩都满足缩尺比。

人为引入额外的初始弯矩之后, 使弯矩值增大, 则可以缩小应力缩比尺与1 之间的差距, 进而缩小厚度尺寸过大带来的影响。虽然并不能使其与完全缩比模型的响应相同, 但能在一定程度上接近。基于此, 文中提出了引入初始弯矩的思路,主要是为了解决不完全几何相似箱型梁模型因为厚度过大导致抗弯刚度太大, 使得模型水下爆炸试验的结果过低估计水下爆炸威力的问题。

以一箱型梁为例, 文中建立了一种能方便进行弯矩幅值和分布可控的初始弯矩引入方法, 使得在水下爆炸作用前, 箱型梁的总纵弯矩与完全几何相似模型的总纵弯矩量级基本一致, 以保证模型的应力相似, 从而保证按相同缩比尺度设计的水下爆炸载荷的作用结果更具参考性。基于该方法开展对比试验, 通过试验结果分析发现, 引入初始弯矩能抵消模型板厚对箱型梁在水下爆炸作用下发生变形的影响, 且不同初始弯矩条件下箱型梁的整体和局部变形模式不同, 在开展船舶缩比水下爆炸试验时有必要关注弯矩的作用。

1 箱型梁基本参数

箱型梁是水下爆炸试验经常采用的结构模式,通常为简单的平底薄壁箱型结构, 如图1 所示。其关键尺寸包括箱型梁的长度L、宽度B、深度H、薄板厚度T和隔板数量s。为直观起见, 下面以某具体箱型梁为例对不同方法所引入的初始弯矩进行说明。计算箱型梁基本参数如表1 所示。

图1 箱型梁整体及横剖截面示意图Fig. 1 Schematic diagram of the whole and transverse sections of the box girder

对于大多数船只而言,H/B的范围约为0.6～0.8,B/L的范围约为0.1～0.2。表1 中采用箱型梁的几何参数选取基本处于这一范围。Sy为箱型梁横剖截面的截面静矩;I为截面惯性矩; 整个箱型梁由厚度一致的Q345 钢板焊接而成,σ0为其屈服极限;ρs为其密度;Mu为截面的极限弯矩。对于任意截面的梁而言, 都有承受弯矩作用的极限。极限弯矩的计算方式为

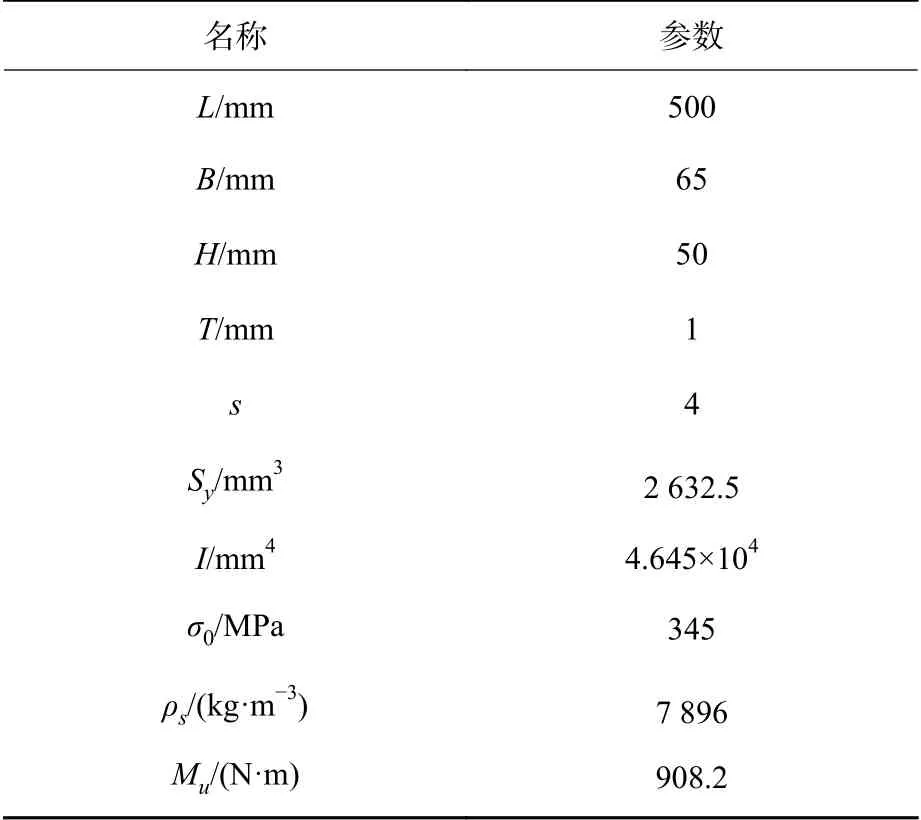
表1 箱型梁基本参数Table 1 Basic parameters of box girder

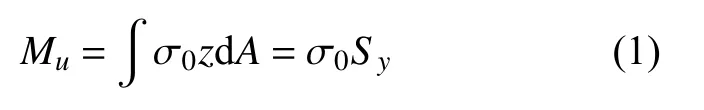
亦即, 材料强度和横截面的几何参数决定了梁截面的极限弯矩。

2 不同状态下初始弯矩

2.1 箱型梁静水弯矩

对于漂浮在水面的船只而言, 弯矩产生的本质是由于重力和浮力沿船长度方向分布不均匀所致。因此根据这一原理计算箱型梁的弯矩。当箱型梁自由漂浮在水面时, 通过重力和浮力达到平衡, 此时箱型梁的吃水深度为

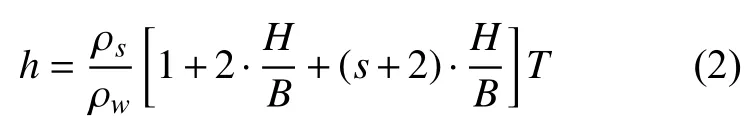
式中,ρw为水的密度。静水状态下箱型梁的重量和浮力分布如图2 所示。

由箱型梁的重量和浮力分布得到其剪力和弯矩分布, 如图3 所示。根据弯矩结果(图3(b)),可知箱型梁静水弯矩的极值Mm出现在梁的中部,Mm≈−0.018 N·m。将该值与表1中箱型梁的极限弯矩Mu比较, 得到静水条件下|Mm/Mu|仅约为0.002%,对于实际船舶而言, 其总纵弯矩一般可以达到其极限弯矩的1/100～1/10 量级, 即静水弯矩相比箱型梁本身的极限弯矩而言微乎其微。如果直接在这种状态下进行水下爆炸试验, 过大的弯矩裕量会使箱型梁抗水下爆炸弯矩的能力变大。

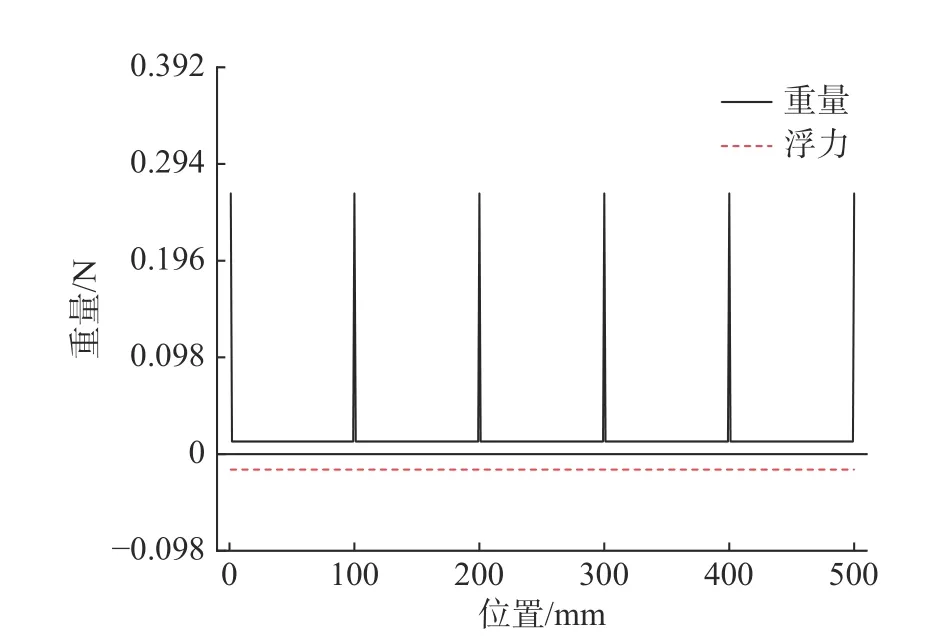
图2 箱型梁的重量和浮力分布Fig. 2 Weight and buoyancy distribution of the box girder

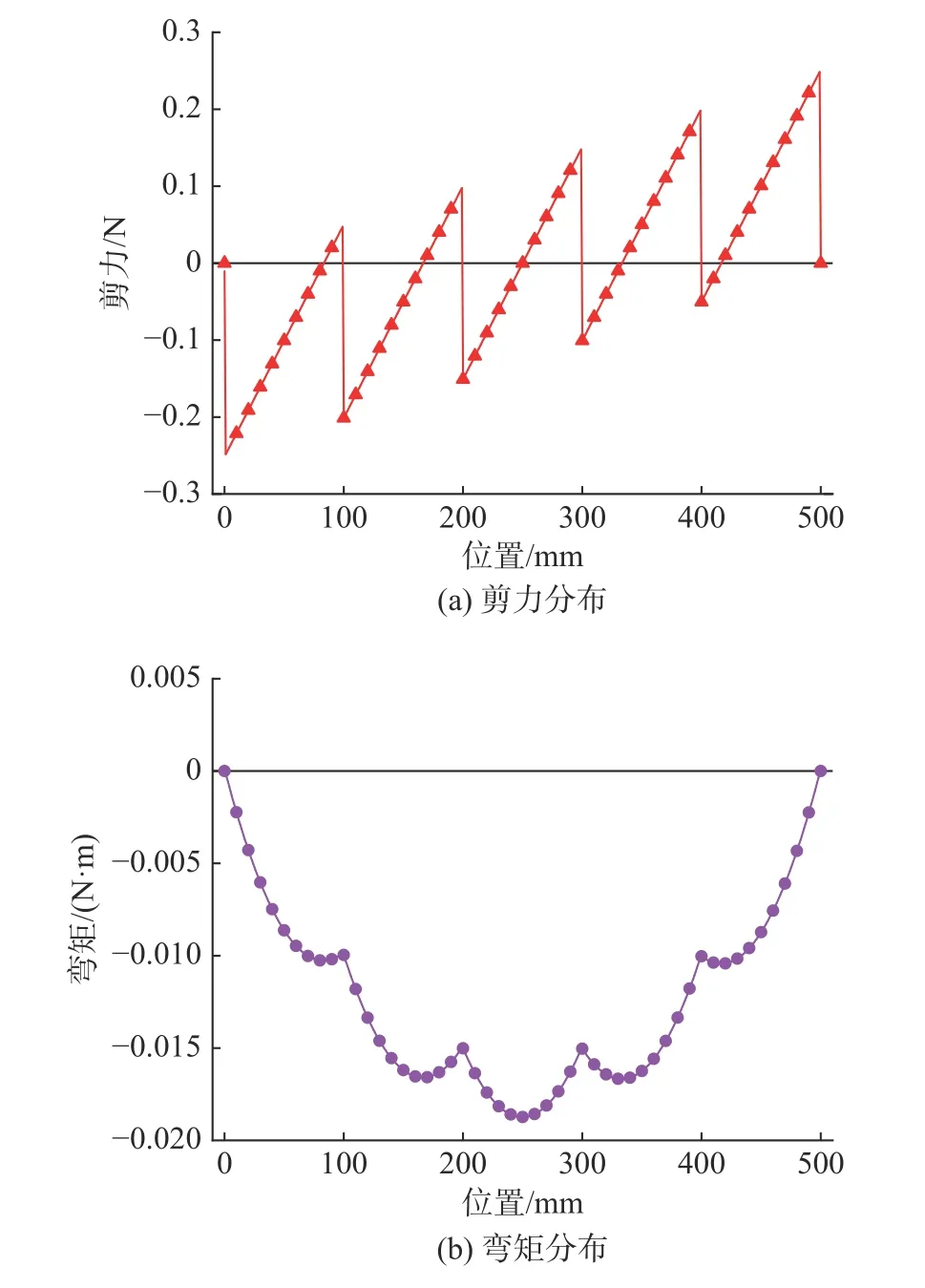
图3 箱型梁剪力和弯矩分布Fig. 3 Shear force and bending moment distribution of the box girder

2.2 悬挂配重下弯矩设计

为了提高箱型梁中的弯矩量级, 产生了采用悬挂配重的想法, 即在不改变板厚的情况下, 通过悬挂和配重的方式增大箱型梁的弯矩。

悬挂配重示意图如图4 所示。悬挂可以使箱型梁获得额外向上的力, 因此配重量不受剩余排水量限制。通过合理设计悬挂点位置、配重大小和分布, 可以实现不同的弯矩幅值和分布形式。

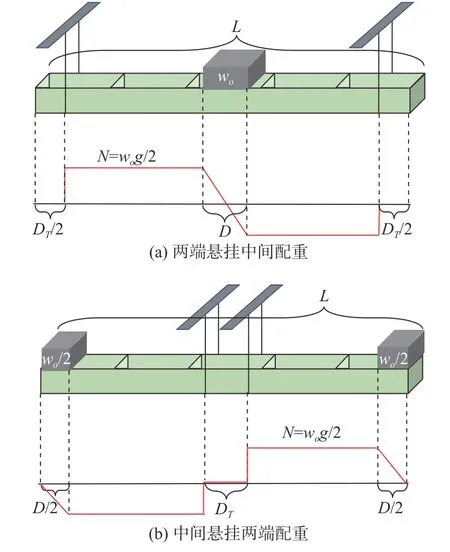
图4 悬挂配重下箱型梁内剪力分布示意图Fig. 4 Shear distribution in the hang-weight box girder

如果忽略模型因为自身重力和浮力引起的弯矩, 则可以根据悬挂处的拉力和超重配重的重力直接计算出箱型梁的弯矩。中间配重两端悬挂时,剪力分布如图4(a)所示, 其中悬挂点到端面的距离为DT/2, 配重区域的长度为D, 配重量为wo, 则箱型梁的最大弯矩为

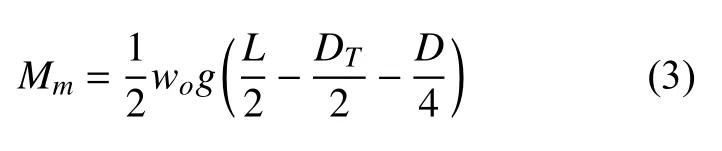
两端配重中间悬挂时, 剪力分布如图4(b)所示, 同理可得箱型梁的最大弯矩。

根据式(3) , 可以很方便地对配重和悬挂方案进行设计。令|Ms/Mu|=k,DT/L=α,D/L=β, 则所需的配重量为

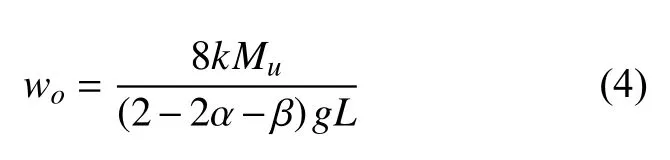
例如, 当α=0,β=1/5, 要想达到k=1%, 需要的配重仅约为wo=8.24 kg。这样就解决了引入弯矩的量级问题。

对于弯矩分布问题, 则可以通过调节悬挂点位置和配重区域来解决。例如, 要实现船级社规范中的弯矩分布[15], 两端悬挂时, 则可以将悬挂点设在两端, 且在距离箱型梁尾部0.4L前和在0.65L后设置配重; 中间悬挂时, 则可将悬挂点设在0.4L和0.65L处, 且在两端设置配重。图5 所示为wo=17.4 kg 时, 按上述2 种悬挂配重方案实现的剪力和弯矩分布。

采用悬挂配重的方法能在不缩小板厚的情况下, 使箱型梁所受的弯矩获得可观增大, 且能根据需要设计悬挂点和配重区使弯矩形成特点分布。另外, 在进行箱型梁水下爆炸试验前, 进行悬挂和配重是很容易实现的。

3 试验开展和结果

3.1 试验基本情况

根据上述分析, 采用悬挂配重可以有效增加箱型梁的初始弯矩, 因此采用这种方式给箱型梁引入初始弯矩, 然后再开展水下爆炸试验。试验所采用箱型梁的参数与表1 一致。设计了4 种不同初始弯矩分布的工况, 其中: 工况1 无配重, 箱型梁自然漂浮状态; 工况2、3 采用中间悬挂的方式(图4(b)), 箱型梁处于中拱状态; 工况4 采用两端悬挂的方式(图4(a)) , 箱型梁处于中垂状态。各工况具体的悬挂位置、配重区域情况和弯矩极值如表2 所示。

试验在2 m×2 m×2 m 的水箱内开展, 炸药采用Φ15 mm×12 mm 的柱形黑索金, 质量为2.77 g,试验时将炸药置于箱型梁跨中正下方10 cm 处。试验中, 在炸药所处深度设置了自由场水中压力传感器进行冲击波压力监测, 在水箱外设置了高速摄像机对水中的爆炸现象进行记录。图6 为试验场景和箱型梁悬挂配重实景照片。

3.2 试验结果与分析

图7 为高速摄影记录各个工况下典型时刻的画面, 由于工况3 和工况2 的过程较为相似, 因此只给出了工况2 的结果。其中,t=0 ms 为炸药起爆前的画面。t=0.2 ms 时箱型梁已经受到了冲击波的作用, 并由于水面和箱型梁底部的反射作用在水中形成了空化区。当空化消失时, 爆炸形成的气泡已经接触到箱型梁, 且箱型梁的变形几乎已经完成。t=3.8 ms 时, 由图7(a)可以看到无配重的箱型梁在爆炸作用下已经飞离了液面; 而在图7(b)中, 工况2 的箱型梁发生向上位移, 且出现了较为明显的整体弯折; 在图7(c)中, 工况4 的箱型梁也发生了向上位移, 但整体位移幅度较小, 且未发现箱型梁出现整体弯折。

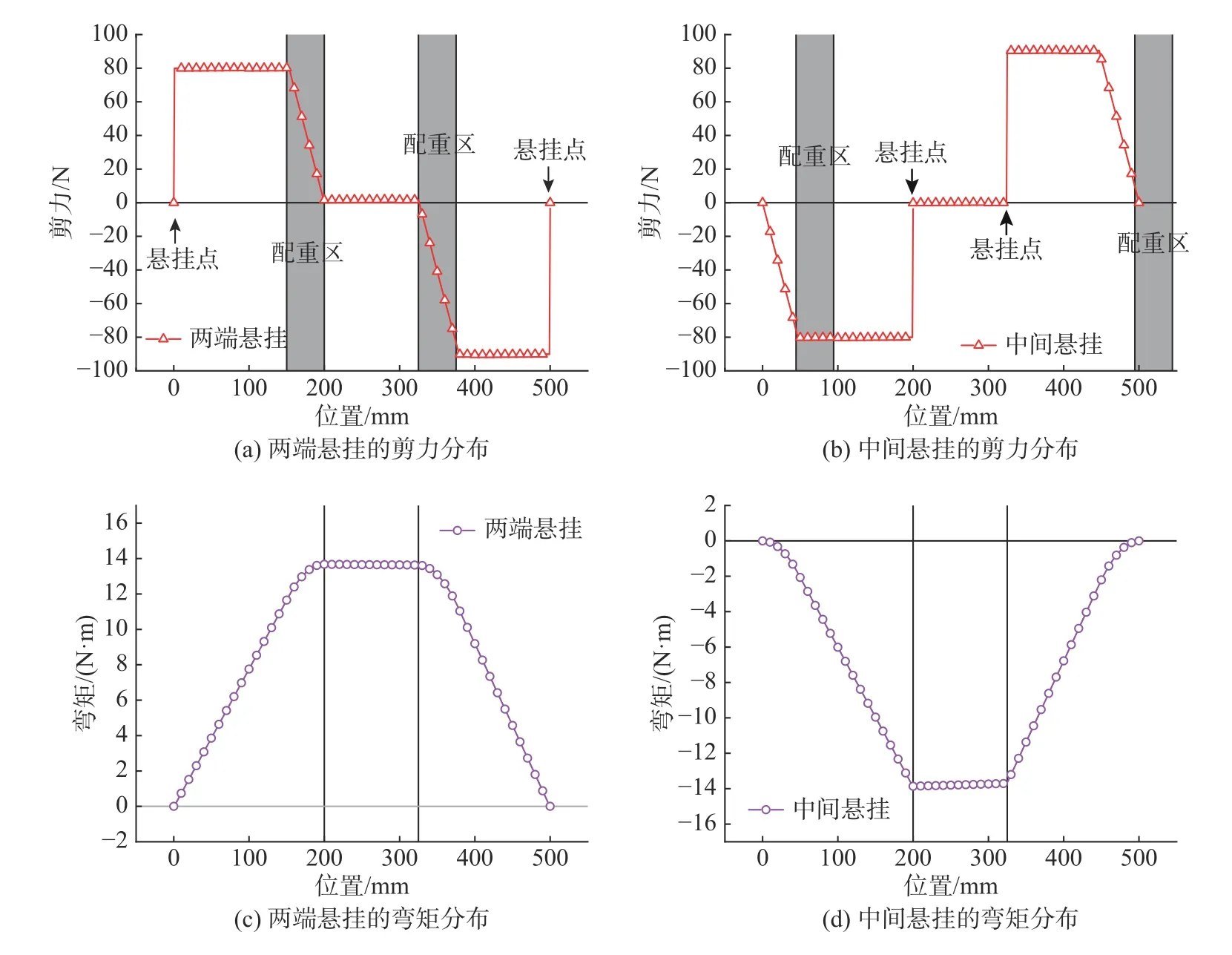
图5 悬挂配重wo=17.4 kg 时剪力和弯矩分布Fig. 5 Shear and bending moment distribution in hang-weight box girder with hang-weight is 17.4 kg

表2 箱型梁水下爆炸试验工况Table 2 Conditions of the underwater explosion test of box girder

图6 箱型梁水下爆炸试验照片Fig. 6 Photos of the box girder explosion experiment

不同工况下箱型梁的整体变形结果如图8 所示。在工况1 中, 箱型梁没有发生明显的整体弯折变形, 仅在其底部发生了轻微的局部凹陷变形; 在工况2 中, 箱型梁发生了明显的整体弯折, 底部发生了严重的凹陷变形, 侧面发生了屈曲变形; 工况3 与工况2 箱型梁的变形现象类似, 区别在于弯折的程度不同, 根据测量: 工况2 中(Hm−He)=46.00 mm,工况3 中(Hm−He)=42.38 mm; 工况4 中, 箱型梁没有发生明显的整体弯折变形, 但其底部的凹陷变形更明显, 侧面也发生了内凹屈曲变形。

图7 箱型梁水下爆炸作用过程典型时刻Fig. 7 Underwater explosion action process of the box girder at typical moment

根据图7 的动态过程和图8 的变形结果可知,不进行配重时, 如图4(a), 图7(a) 和图8(a)所示, 在水下爆炸载荷作用下, 箱型梁发生塑性变形的程度很低, 爆炸作用到箱型梁上的能量更多转换为箱型梁的动能, 相应地, 需要通过变形吸收的能量就少了很多。造成这一现象的主要原因是板厚太大, 使得箱型梁的抗弯刚度大, 在自由漂浮状态下,受到爆炸载荷作用时, 过大的抗弯强度使得箱型梁足以抵抗爆炸引起的弯矩, 这使得相当大比例的爆炸能量转化为箱型梁的动能, 相应地, 转化为塑性变形的能量会减少。运动耗能的优先级高于整体变形耗能。

通过悬挂配重的方式在箱型梁中引入一定量级的弯矩后, 模型的变形程度显著增加, 且在不同的弯矩分布模式下箱型梁的破坏模式也不同。当采用中间悬挂两端配重的方式使箱型梁处于中拱状态时, 如图7(b)所示, 在水下爆炸载荷作用下箱型梁呈现整体弯折和局部变形的双重破坏模式,如图8(b)所示。且根据工况2 和工况3 中箱型梁弯折程度的对比, 配重越大, 初始弯矩幅值越大, 箱型梁最终的整体弯折程度越大。当采用两端悬挂中间配重的方式使箱型梁处于中垂状态时, 箱型梁的破坏模式则以局部变形为主, 整体弯折变形不明显。

图8 箱型梁整体变形结果Fig. 8 Deformation results of the box girder

通过上述试验结果的对比可以发现, 采用悬挂配重方式引入初始弯矩后, 在相同的水下爆炸载荷作用下, 箱型梁的变形模式发生了较为显著的变化。在中垂状态下主要是局部凹陷变形模式,在中拱状态下为整体变形弯折和局部凹陷组合变形模式。这2 种弯矩状态下的变形程度均比不考虑弯矩作用时更大, 从变形结果看, 水下爆炸的毁伤效果更为显著。

4 结束语

采用悬挂增重的方式, 引入量级可观的初始弯矩能一定程度上抵消模型板厚对箱型梁在水下爆炸作用下发生变形的影响, 且不同初始弯矩条件下箱型梁的整体和局部变形模式不同, 在开展船舶缩比水下爆炸试验时有必要关注弯矩的作用。当然, 船舶缩比水下爆炸试验并不能因为引入初始弯矩而使不完全几何相似模型的响应结果与完全几何相似模型严格一致, 关于其相似规律的深入分析还有待开展。

[1]S hin Y S. Ship Shock Modeling and Simulation for Far-Field Underwater Explosion[J]. Computers amp; Structures, 2004,82(23-26): 2211-2219.

[2]L iang C C, Tai Y S. Shock Responses of a Surface Ship Subjected to Noncontact Underwater Explosions[J]. Ocean Engineering, 2006, 33(5-6): 748-772.

[3]L i H, Zhang Y, Zhang Z. Damage Characteristics of Boxlike Beam as a Bulk Subjected to Underwater Explosion in Near-Field[J]. Acta Armamentarii, 2012, 33(5): 611-616.

[4]W ang H, Zhu X, Cheng Y S, et al. Experimental and Numerical Investigation of Ship Structure Subjected to Close-in Underwater Shock Wave and Following Gas Bubble Pulse[J]. Marine Structures, 2014, 39: 90-117.

[5]Z hang Z, Wang Y, Zhao H, et al. An Experimental Study on the Dynamic Response of a Hull Girder Subjected to Near Field Underwater Explosion[J]. Marine Structures, 2015, 44:43-60.

[6]W ang H, Cheng S Y, Liu J, et al. Damage Evaluation of a Simplified Hull Girder Subjected to Underwater Explosion Load: A Semi-Analytical Model[J]. Marine Structures, 2016,45: 43-62.

[7]G an N, Yao X L, Liu L T, et al. Research on Overall Damage Characteristics of a Hull Girder under Explosion Bubble Collapse[J]. Ocean Engineering, 2019, 188: 106315.

[8]H e Z, Chen Z, Jiang Y, et al. Effects of the Standoff Distance on Hull Structure Damage Subjected to Near-field Underwater Explosion[J]. Marine Structures, 2020, 74: 102839.

[9]Z hang Z, Wang Y, Zhang L, et al. Similarity Research of Anomalous Dynamic Response of Ship Girder Subjected to Near Field Underwater Explosion[J]. Applied Mathematics and Mechanics, 2011, 32(12): 1491-1504.

[10]K im Y, Lee S, Kim J, et al. Development of a Generalized Scaling Law for Underwater Explosions Using a Numerical and Experimental Parametric Study[J]. Structural Engineering and Mechanics, 2021, 77(3): 305-314.

[11]Z hang X. Similarity Criteria for Experiment of Underwater Explosion[J]. Journal of Ship Mechanics, 2007, 11(1): 108-118.

[12]谢 建林. 瞬态载荷作用下弹塑性结构动响应相似性研究[D]. 哈尔滨: 哈尔滨工程大学, 2008.

[13]苏 罗青. 舰船总体与局部强度水下爆炸实验方案研究[D].哈尔滨: 哈尔滨工程大学, 2011.

[14]Z hang H, Yue Y, Su L, et al. Model Experimental Scheme for Longitudinal Strength of a Warship Subjected to Underwater Explosion[J]. Journal of Vibration and Shock, 2012,31(6): 175-180.

[15]中 国船级社. 钢质海船入级规范[S]. 北京: 中国船级社,2018.

An Experimental Method for Box Girders Subjected to Underwater Explosions Considering the Initial Bending Moment

ZHENG Jian,LU Fang-yun,LI Xiang-yu,LIANG Wen,CHEN Rong

(College of Liberal Arts and Science, National University of Defense Technology, Changsha 410073, China)

Box girders are commonly used in underwater explosion experiments on scaled ships. Owing to the challenges associated with materials and welding techniques, the plate thickness of the box girders is always greater than that of a completely geometrically similar model, which leads to increased bending stiffness. Therefore, underwater explosion tests based on these models will underestimate the power of underwater explosions and test results are difficult to map directly to accurate models. To offset the influence of excessive bending stiffness, a method that can easily control the amplitude and distribution of the introduced initial bending moment is proposed. Based on the results of a set of comparative experiments, we determined that the proposed method can reduce the influence of model plate thickness and can be used to study the influence of the bending moment on the underwater explosion responses of box girders. This method can provide a reference for the design of underwater explosion experiments on scaled ships.

underwater explosion experiment; bending moment; box girder

TJ410; U674

A

2096-3920(2022)03-0398-07

10.11993/j.issn.2096-3920.2022.03.017

郑监, 卢芳云, 李翔宇, 等. 一种考虑初始弯矩的箱型梁水下爆炸试验方法[J]. 水下无人系统学报, 2022, 30(3):398-404.

2022-03-08;

2022-05-07.

国家自然科学基金(11872376,12172380); 湖南省杰出青年基金(2022JJ10058).

郑 监(1993-), 男, 博士, 主要研究方向为水下爆炸.

(责任编辑: 许 妍)