水下爆炸声学效应研究现状与展望

郭 锐, 俞旸晖

水下爆炸声学效应研究现状与展望

郭 锐, 俞旸晖

(南京理工大学 机械工程学院, 江苏 南京, 210094)

水下爆炸声源具有功率高、频带宽、无指向性等特点, 在海洋资源探测、水文环境反演、水下微小隐身目标探测和水声对抗干扰等领域有着广泛的应用前景。文中综述了水下爆炸声源特征中冲击波及理想气泡脉冲的声辐射机理, 分析了声场模型中用于描述水下爆炸声源传播和混响效应的水声传播模型与混响模型, 总结了水下爆炸声源的典型信号分析方法及其声学特性, 并结合水下爆炸声源的特点介绍了相关的典型工程应用。最后, 展望了水下爆炸声学效应研究在高能炸药材料水下爆炸的能量转换机制和致声机理、声混响强度预报、阵列多脉冲爆炸声源工程应用等方面的发展趋势, 为水下爆炸声学效应的进一步研究提供参考。

水下爆炸; 致声机理; 声场模型; 声学特性

0 引言

声波是目前可知唯一可以在水介质中远距离传递信息的载体。利用深海信道, 几千克炸药产生的爆炸声在海水中传播几千公里后, 依然可被信号接收装置接收, 因此水声效应已在海洋探索和开发中得到了广泛应用。

由于水介质的特殊性, 炸药水下爆炸特性与空气中爆炸相比要复杂的多。水下爆炸时, 爆炸冲击波波阵面压力和速度在水中传播过程中下降很快, 迅速衰减成强声波。炸药小药量装药水下爆炸所产生的噪声总声源级可以达到200 dB以上, 其频率分布在50 Hz～50 kHz的宽阔范围内, 尤其在10 kHz以下的低频分量具有相当高的声功率, 如图1所示。

图1 25 g黑索金(RDX)炸药水下爆炸声学特性曲线

Urick[1]引述Arons[2]的研究结论指出, 传统炸药材料(如TNT)装药水下爆炸所产生的总化学能中, 约有40%的能量转化为声能辐射到1 m以外的距离上, 具有相当高的声转换效率, 如表1所示[2]。水下爆炸声源因其高声功率和高声转换效率的特点, 已作为一种传统声源被广泛应用于地球物理勘探、反潜回声定位及水声干扰中。

表1 TNT爆炸能量分配表

随着人类对海洋探索的深入, 海洋开发和军事需求进一步促进了水下声源技术的发展, 新型高性能水下声源的作用方式和发声机理已成为各水声强国竞相研究的热点[3-4]。水下爆炸及其扰动传播过程属于大变形、高度非线性、流固耦合的瞬态动态响应, 涉及非常复杂的能量转换过程。目前, 海洋科学已成为我国未来发展的重点领域, 对海洋信息的感知与辨识需求日益迫切。为此, 文中从水下爆炸的致声机理出发, 系统综述了水下爆炸声的发生、传播及声学特性的研究进展, 以期为我国水中爆炸声源技术的发展提供参考。

1 水下爆炸致声机理

由于水介质的特殊性, 炸药水下爆炸特性与空气中爆炸相比要复杂的多。当炸药在均匀、静止的深水中爆炸时, 高压爆轰产物急剧向外膨胀, 在水中形成初始冲击波。同时在爆轰产物与水的界面处反射一稀疏波, 以相反的方向向爆轰产物中心运动。由于水的密度大、可压缩性小, 水中爆炸冲击波初始压力比空气大得多, 空气中爆炸冲击波初始压力在60～130 MPa, 而水中爆炸冲击波初始压力在10 GPa以上, 接近于炸药爆轰区压力。随着水中爆炸冲击波的传播, 其波阵面压力和速度迅速下降, 波形不断拉宽。由于水的体积模量相比空气极高, 当波阵面压力下降约为250 MPa时, 波阵面传播速度已下降至接近声速。在形成初始冲击波的同时, 爆轰产物迅速向外膨胀, 并以气泡的形式推动周围的水沿径向向外运动。气泡压力随膨胀不断下降, 当其膨胀到压力等于静水压后, 在惯性作用下继续向外膨胀直至达到最大体积, 此时气泡内部压力约为静水压的1/5～1/10。而后, 由于外界压力的作用使气泡收缩, 同样由于惯性的作用, 在气泡内压力达到静水压时仍继续收缩, 直到最小体积时又开始膨胀, 如此反复膨胀、收缩, 形成气泡脉动。在气泡脉动过程中, 同时产生稀疏波和压缩波[5]。扩展和崩溃过程重复进行, 直到气泡向上移动到水面或分裂为许多小的气泡时为止[6]。在水下爆炸过程中, 爆炸产生了如图2所示的2种不同的声信号, 一种是持续时间很短, 功率高、频带宽的冲击波脉冲, 另一种是气泡脉动的辐射脉冲, 当声信号或气泡与边界相互作用时, 又会形成新的声信号。

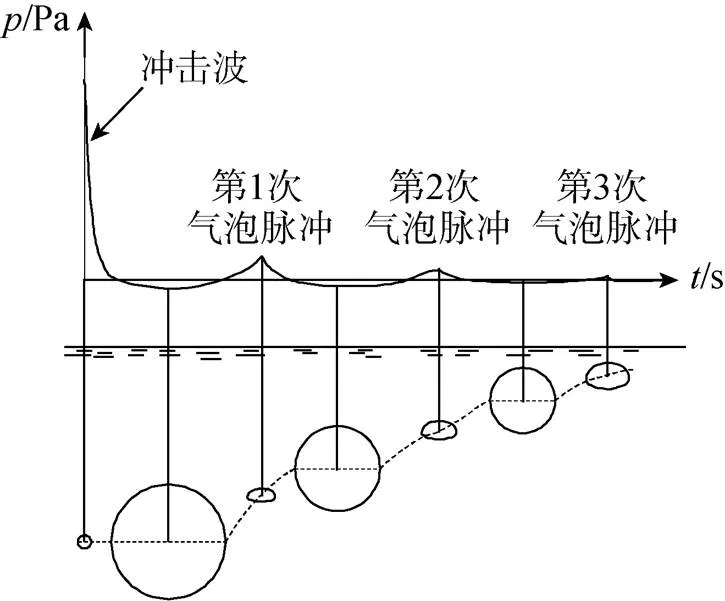
图2 水下爆炸声信号结构与产生过程示意图

水中冲击波的有限振幅效应使得冲击波不同部分以不同的速度传播, 从而导致频谱能量发生转移, 并使波阵面附近的粘性能量损失保持在较高水平。冲击波传播过后, 气泡的迁移、破裂及合并等效应也会影响水下爆炸声辐射过程。与此同时, 水下爆炸还涉及多物理场之间的耦合作用, 尤其对于含铝炸药, 爆炸气泡膨胀时气体和高温残渣粒子可能喷射进入水中, 当气泡回弹时部分粒子滞后于气泡, 产生了复杂的声辐射特征。目前, 还没有一个完整的理论体系将水下爆炸致声机理阐述清楚, 通常根据流体动力声源辐射思想进行解释。

1.1 流体动力声辐射机理

19世纪中后期, Stokes和Rayleigh就认识到扰动的质量和力作为声源的作用, Lighthill[7]于1952年发现湍流切变应力也可起到声源的作用, 提出了声比拟思想, 从而形成了将质量通量、力源和粘性应力视为噪声源项的广义Lighthill方程

式中:为单位体积内新增质量的速率;f为作用在单位体积流体上任何外部机械力的净力;为粘性应力。

根据式(1), 可将致声机理归结为3种: 脉动体积源致声、脉动力源致声和湍流致声, 分别对应单极子声源、偶极子声源以及自由四极子声源, 不同声源的速度势场参见图3, 图中的、均为空间坐标。

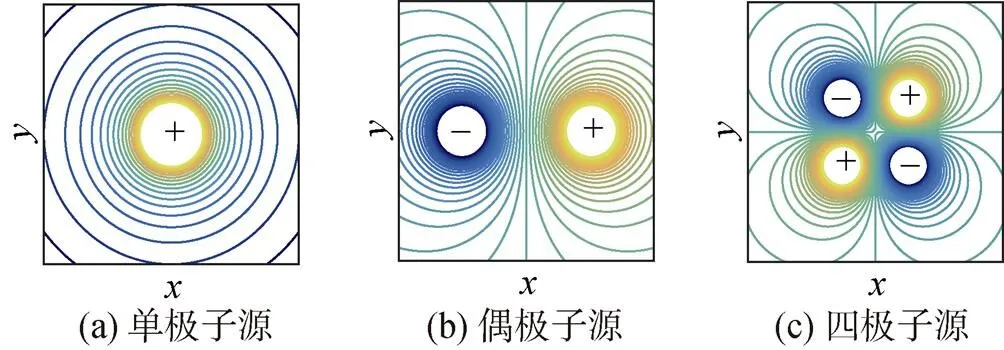
图3 典型流体动力源速度势

单极子声源主要是体积或者质量发生脉动的点源, 其水下声场分布比较均匀, 无指向性; 偶极子声源则是压力脉动以及振动的刚性物体, 其主要特征为声谱具有余弦方向性; 四极子声源主要是湍流运动引起的压力脉动。一般情况下, 前两者经常出现在流体界面层中, 而后者不仅在流体界面层发生, 在流体内部也会同时出现。

1.2 冲击波声辐射机理

目前Lighthill的声比拟理论已被普遍接受, 然而Tam[8]指出当声波考虑有限振幅效应时, 式(1)的左侧应该包含非线性波陡化项, 而流体力学控制方程中普遍存在的守恒概念在声比拟理论中并没有保留, Euler方程描述的激波传播解不能通过求解具有精确四极子项和源的Lighthill方程获得, 这意味着通过Lighthill方程来计算冲击波的辐射过程可能存在一定问题。

1.2.1 冲击波单极子源辐射模型

在20世纪30～60年代, 以欧美、前苏联为首的主要军事强国开展了水下爆炸理论研究, 同时进行了大量的水下爆炸试验和水下核试验, 获得了大量试验数据, 为总结水下爆炸的致声机理奠定了基础。

在水中爆炸冲击波声辐射理论研究方面, 国内外普遍将该辐射过程视为爆炸气泡单极子源的辐射。自20世纪40年代开始, Kirkwood等[9]采用等容爆轰模型对冲击波和气泡脉动部分解耦, 将冲击波的传播转变成气泡表面上动焓的计算, 为冲击波波形描述和波后流场分析提供了理论参考。其后, Kirkwood等[10]对上述理论进行了发展, 提出用能流密度结合冲击波阵面上的压力和速度关系求解波阵面后参数, 这种近似计算方法可由试验直接测量的冲击波超压时程积分, 非常适合将某一距离处的数据推算到其他距离处, 但不能很好地建立冲击波传播与气泡脉动的联系, 在近场计算时易存在误差。Kedrinskii[11]基于瞬时爆轰假设, 考虑水下爆炸气泡界面处压力和焓以指数衰减规律变化, 给出了气泡界面处的初始条件, 在Kirkwood-Bethe假设[9]下得到了任意时刻流场中一点处的动焓与气泡界面处动焓的关系, 由此得到了柱形炸药的冲击波声辐射过程的解。Geers等[12]给出了一种远场冲击波压力的双指数拟合形式, 同时依据声学理论中的脉动球源思想建立了冲击波阶段气泡体积加速度与不同位置处压力分布的超声关系, 该模型将冲击波阶段与气泡脉冲阶段的压力关系分时段表示。李澎等[13]在Kirkwood-Brinkley理论[10]的基础上分析了能流密度-时间曲线的表达式, 并简化了水中爆炸冲击波的传播计算方法, 针对不同距离之间冲击波的压力峰值, 运用实际数据对近似计算结果进行了验证。Wang等[14]根据Tait方程和JWL方程描述相应介质获得了精确气泡膨胀初速表达式, 将流体可压缩性用焓表示, 结合Lezzi-Prosperetti方程给出了比Geers-Hunter模型[12]更贴近实际的单极子源膨胀过程控制方程, 通过求解该方程可以获得冲击波辐射压力。

水下爆炸冲击波在传播到一定药包半径距离处后, 可将冲击波波头视为一个带有间断的压缩波。当冲击波传播到距爆心约90倍药包半径处的时候[15], 冲击波马赫数(/0)接近于1。Weston[16]指出, 水下爆炸形成的声信号在100 yd范围内需要考虑有限振幅效应和耗散, 而这些效应在100 yd之外可以忽略。

在冲击波辐射参数半经验关系拟合方面, Cole[17]所在的水下爆炸研究实验室对TNT等理想炸药的球形药包水下爆炸冲击波进行了系统试验研究, 验证了Kirkwood等提出的冲击波传播理论, 揭示了爆炸参数之间的关系, 其提出的半经验半理论公式至今仍被广泛应用, 而该半经验关系的适用TNT等效爆距范围随后被Arons[18]、Blaik等[19]分别推广至794.40 m/kg1/3和15 868 m/kg1/3。Cole提出的TNT炸药水下爆炸压力衰减公式如式(2)所示。

式中:为冲击波压力峰值;为衰减常数;为冲击波压力;为测距;为药包质量;为冲击波到达时间。

Alpaslan等[20]对炸药在海洋环境下的爆炸压力进行了测量, 记录的峰值超压通过对数和线性2种不同形式的最小二乘方法重新确定经验公式常数, 新确定的常数与Cole经验公式的常数略有不同。

Arons[18]测量了远距离处的水下爆炸冲击波信号, 指出冲击波超压峰值幂函数的斜率与无量纲量1.0的偏离是由于能量的耗散和波形的传播造成的。同时, Arons指出在689 kPa(100 psi)以上的压力范围内, Kirkwood-Bethe理论[9]很好地解释了式(2)中超压峰值幂函数的斜率为1.13的原因, 即耗散主要出现在激波阵面的不可逆压缩中, 但在传播到更远的距离时, Kirkwood-Bethe理论产生了一个对数形式的解, 与实际结果并不相符, Temkin[21]认为这可能是冲击波在水中传播时非线性效应导致的。

1.2.2 弱冲击波辐射中的非线性效应

水中冲击波在传播过程中会在很远的距离上仍然保持锐利的间断面, 这种波形被DuMond等[22]称为N形波。在一定距离内, 冲击波阵面处的峰值衰减速率比线性声学预测的更快。虽然此时的波阵面峰值超压一般较低, 但其非线性效应依然不可忽略。当保留声压的2阶小量时, 通过引入非线性声学中的非线性系数0构建一个如图4所示的简化模型进行分析。

DuMond等[22]于1946年通过观测时间-压力剖面中的周期随传播的变化率来测量N形波绝对振幅的方法, 研究了这种波形在理想空气介质中的传播过程, 该方法给出了在大传播距离上距离、振幅和观测周期之间的绝对关系。Landau等[23]论述了声波间断形成的原因, 通过简单波渐近表示的方式给出了速度间断值及其间断位置所满足的关系。

Wright[24]、Temkin等[25]分别通过短球面冲击波和平面冲击波对上述理论进行了试验验证。在图4表示的结构中, 球面理论给出了当距离大于冲击波脉冲长度1时球面波的参数, 且

式中:1为所选择的距离炸药较远的冲击波阵面到达位置, 满足1>>1;1为冲击波阵面传播到该处时的正压脉宽(空间量);1为该位置处冲击波阵面后的峰值压力。

图4 N形波空间-压力剖面

考虑声速1阶小量后, 弱冲击波可借助非线性声学中的声学近似方法描述, 非线性效应不断将低频能量转移到高频, 冲击波能一直保持锐利的间断面, 但随着传播距离持续增大的高频谐波分量并不符合真实情况。因此还需要考虑介质的黏滞热传导效应, 此时真实冲击波宽度必须考虑, 黏滞吸收系数与波数、非线性系数相互竞争, 最终导致冲击波信号在远场时具有明显的上升时间。

1.3 气泡脉冲声辐射机理

气泡脉冲压力是在炸药水下爆炸的准静态过程中辐射出来的, 取决于气泡的脉动与迁移[26]。大量研究结果表明, 气泡在水中的体积振动可作为质量-弹性系统来处理, 其可视作单极子源, 声辐射效率相比于偶极子源和四极子源高[6], 是冲击波辐射之外的另一个重要的水下声源。但在有的应用过程中, 有时还需额外滤去气泡脉冲以提取纯净的爆炸声信号[27-29]。

实际的气泡振动过程中受多种因素影响, 气泡脉冲声辐射机理是根据水下多种声辐射机理总结而成的, 包括水下气泡振动方程[30-31]、湍流噪声[32]、热声效应[33]、单极子源噪声、偶极子源噪声以及四极子源噪声原理等[34]。

国内外在气泡脉冲声辐射领域的研究方法以模型分析和试验研究为主, 其中模型分析有助于研究简单的模型, 揭示其机理。在推导气泡运动的理论模型过程中, 通常认为在第1个脉动阶段压缩效应和黏性效应均不重要, 往往忽略可压缩效应和黏性效应。

Besant[35]首先提出了一个球形气泡在无粘、无限空间、不可压缩液体中运动的问题, 建立了分析模型预测了液体中任意一点的压力及气泡溃灭时间。Rayleigh[36]在Besant球形气泡膨胀和收缩运动模型的基础上加入了气体的等温状态方程, 通过对连续性方程进行积分获得径向速度场的方式得到了无限流域中的气泡解, 该数学模型表明气泡表面速度是通过假定液体所做的功等于气泡运动的全部动能得到的。Plesset[37]则利用连续性方程和运动方程得到了微分形式的气泡运动方程, 即Rayleigh-Plesset(RP)方程。利用此方程研究气泡的馈灭过程, 在气泡的半径较大时, 所得结果具有一定准确性, 但当气泡溃灭至很小的半径时, 由于没有考虑气泡的含气量、表面张力、黏滞性及可压缩性等因素的影响, 将会导致一些不合理的结果。

为了对Rayleigh理想气泡的运动方程进行修正, 研究人员从不同的角度修正了RP方程, 得到了考虑不同因素的气泡运动方程。Poritsky[38]第1个讨论了液体粘性对气泡行为的影响, 同时讨论了考虑及不考虑表面张力条件下气泡溃灭时间的有限性。Noltingk等[39-40]在考虑气泡内气体成分影响的基础上修正了RP方程。综合以上成果, Lauterborn[41]总结出著名的气泡运动方程

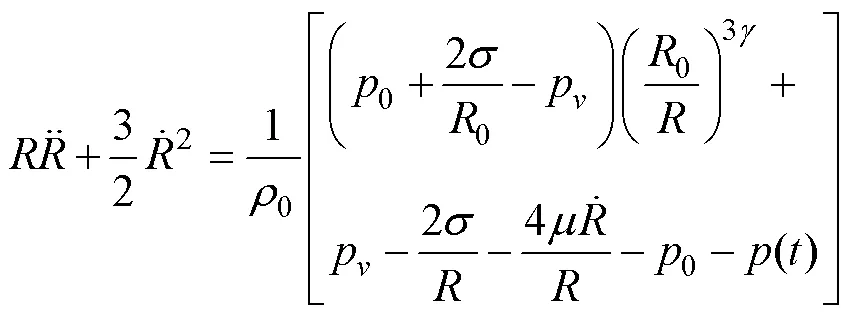
基于上述理论, 将方程与Bernoulli方程联立可得气泡作为单极子源在流场中辐射出的声压。

2 水下爆炸声场模型

水下爆炸声在水中传播、反射、被接收以及目标探测和定位等规律, 可以用水声模型加以描述。水声模型包括环境模型、声场模型和声呐性能模型3类[42], 模型之间的关系如图5所示。

2.1 水声传播模型

水声传播模型用于描述声源发出的声波在海洋环境中传播产生的能量衰减和波形畸变的规律, 对于噪声、混响以及最终的基于声呐性能的更高层次的建模是不可或缺的。目前, 传播模型主要分为5种不同的技术[43], 包括射线理论技术、简正波方法、多途展开技术、波数积分方法和抛物方程近似等。根据不同的条件还出现了混合模型[44-46], 各类方法适用的场景如表2所示[47]。

图5 3类水声模型关系示意图

水下爆炸冲击波传播到一定距离后, 可通过线性声学理论处理, 其在水中的传播过程可利用线性波动方程描述。在不同的初始条件和边界条件下, 由波动方程推导出不同的声学传播模型, 常见的有射线理论模型和简正波模型。

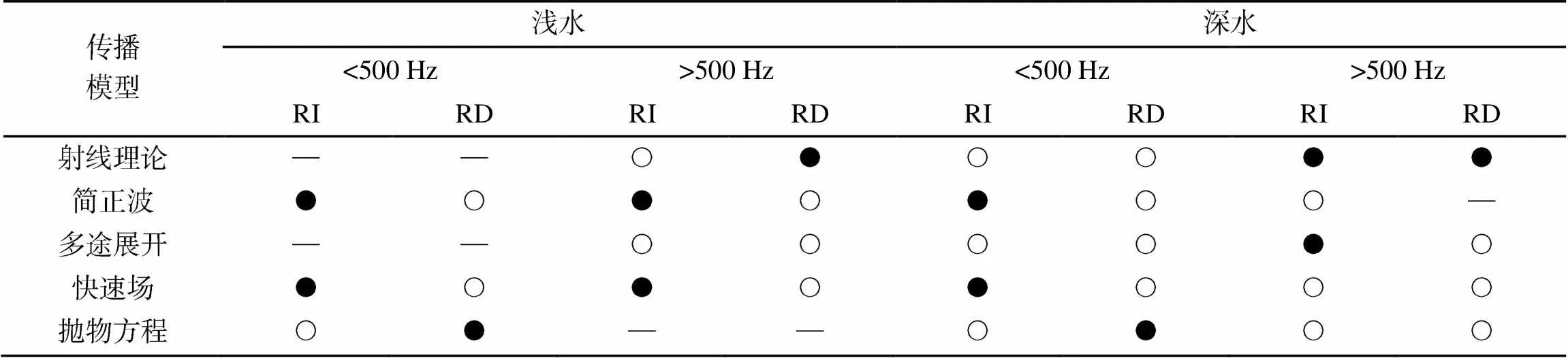
表2 各类水声传播模型适用场景对照表

注: 表中RI表示环境与水平距离无关; RD表示环境与水平距离有关; “●”表示传播模型既在物理上是准确的, 又在执行速度上是实用的; “○”表示在准确性或执行速度上存在限制; “—”表示不可行。

当信号幅值在一个波长内的改变量很小时, 可以得到程函方程和强度方程, 这是射线声学的基本方程

式中:(,,)为程函, 长度量纲;0为参考点声速;(,,)为空间某点的声速;(,,)为空间某点折射率;(,,)为声压幅值。

通过求解方程(6)可得声线传播过程的近似解。Porter[48]于1987年编写了基于射线理论的BELLHOP模型, 该模型基于几何和物理的传播规律, 可以跟踪多种波形类型的射线在海洋环境中的传播轨迹, 从而达到预测声压的目标。该模型还可以输出传播损失、本征声线、到达和接收时间序列等信息, 被指定为美国海军海洋预报10～100 kHz频带声传播的标准模型[49]。吴丽丽等[50]基于2013年7月在西太平洋进行的远程声传播试验, 使用抛物方程模型和射线模型分析解释了125 m深拖曳换能器发射的线性调频声信号(260～306 Hz)和水下1 000 m深爆炸产生声信号的远程脉冲声传播现象。

1948年, Pekeris[51]发展了海水和沉积物的两层模型, 用简正波理论解决了水下爆炸导致的声源传播问题。为了研究水平变化缓变的海洋环境下爆炸声脉冲的频散特性, Pierce[52]首先提出绝热简正波理论计算方法, 但该理论忽略了由于水平变化导致的简正波耦合, 不适用于水平变化剧烈的海洋环境。Evans[53]则在考虑简正波耦合的基础上修正了绝热简正波理论, 可用于水平变化较大的环境, 但本征值、本征函数和耦合系数的计算较为困难。20世纪70年代后期, 一些简正波模型被广泛用于预报海洋传播损失, 但对特定声速剖面存在数值不稳定性, 且不能计算完整模态序列。20世纪80年代起, Michael等[54]为了解决这些问题, 发展了一种新的算法构成Kraken简正波建模的基础。张仁和等[55-56]提出并完善了计算深海声场的广义相积分简正波理论(WKBZ简正波理论)与计算浅海声场的波束位移射线(beam displacement ray mode, BDRM)简正波理论, 提高了计算精度, 计算速度也比国际上流行的算法快1～ 2个数量级。

2.2 声混响模型

水下爆炸产生的声信号在传播过程中, 经过分布在水面、水中和水底的散射元的散射后形成混响。水下爆炸产生的脉冲压力波持续时间较短, 受海水介质的特殊性、海洋特有的不均匀性以及其他外界因素(如海面、水深、海底介质、海底地形)的综合影响而产生的声混响效应会使脉冲爆炸声在水中能持续一段时间。

由于水下爆炸冲击波是一种宽频短时脉冲信号, 持续时间短(仅有几百微秒), 频率范围广(从几赫兹到几十赫兹), 并且频率特性不稳定。除了体积混响外, 当不满足获取理想爆炸声信号的3个限制条件时[57], 水听器测得的信号往往存在边界效应干扰, 即信号为混响信号。水下爆炸声混响的常用计算模型有射线方法和简正波方法等。

Bucker等[58]最先使用简正波理论分析均匀浅海中的混响, 其通过将简正波分解为上行波与下行波, 并将下行波与海底散射相联系的方法进行计算。吴承义[59]则利用射线方法计算了浅海的平均混响强度。张仁和等[60]将Bucker等的方法[58]推广到非均匀浅海环境, 利用简正波理论计算了浅海的平均混响强度。Ellis等[61]建立了将Lam-bert散射定律与基于Kirchhoff近似的表面散射函数相结合的三维散射模型, 在美国海军水下系统中心(Naval Underwater Systems Center, NUSC)的通用声呐模型中增加了所提出的散射模型, 建立了一种基于本征射线求取的海底双基地混响模型, 并通过了试验验证。Peter等[62]利用射线理论计算了水下爆炸声混响, 由于该方法不考虑频率因素, 所以可避免由频率引起的计算量较大的问题。然而射线理论的基础是求取本征声线来表示信号的传播路径, 对于深水区域, 求取本征声线的计算量较小, 而对于浅水区域, 由于水面和水底的多次反射和散射引起的多途效应, 求取本征声线的计算量将大幅增加。因此为了减小计算量, 惠娟等[63-64]基于射线方法和Lambert散射定律, 在等声速环境假定下利用椭圆和椭球的几何性质, 即椭圆和椭球面上任意1点到2个焦点的距离之和为常数, 给出了二维和三维收发分置混响平均强度的预报公式, 不需要求取本征声线, 大大减小了计算量。盛振新等[65]将惠娟的双基地混响模型推广到一般椭球公式控制下的混响模型, 对海底界面混响进行了讨论。Guo等[66]在盛振新提出的混响模型的基础上考虑了海面、海底界面散射效应及常声速梯度环境, 建立了双基地界面混响预报模型, 对2种距离处的声混响进行了计算, 并探讨了界面散射及声速梯度对混响场的影响, 模型如图6所示(假设负声速梯度条件)。

3 水下爆炸声学特性

水下爆炸相比于烟火药[67]、气枪[68]等能在水中形成高声源级、高功率、宽频带的声信号,信噪比很高, 但爆炸冲击波压力衰减快, 声信号持续时间较短。为了将水下爆炸声信号应用到实际工程领域中, 需要对水下爆炸的声信号特性进行分析研究。

3.1 信号分析方法

水下爆炸声信号分析方法是研究水下爆炸声信号声学特性的基础。受限于数字计算机的不成熟, 早期一般采用倍频程滤波对信号进行特征提取以获得信号的频带特性。随着数字计算机和数字信号处理技术的发展, 1965年, Cooley和Tukey提出了快速傅里叶变换(fast Fourier transform, FFT), 此后研究人员常常通过FFT提取数字信号的频率特性对信号进行分析。在信号频率的定义方式上, 目前有2种分类, 一种是傅里叶所提出的稳态频率, 另一种则是Carson提出、Gabor等完善统一的瞬时频率。2种频率定义为不同信号特征提取方法提供了理论基础。

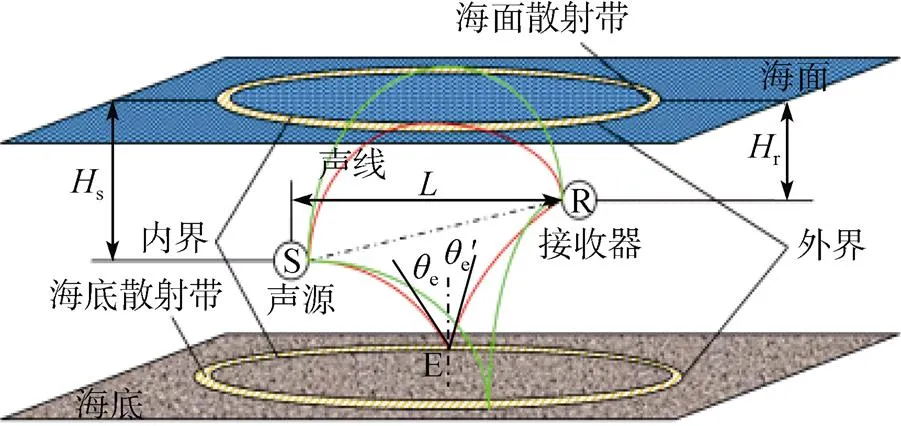
图6 界面散射引起的三维双基地混响示意图

水下爆炸压力信号持续时间短、突变快, 属于非平稳信号, 信号的结构及其频谱都是时变的, 与傅里叶变换建立的理论基础不一致[69-70], 傅里叶变换会高估高频分量的成分。随着信号处理技术的发展, 水下爆炸压力信号的分析方法主要经历了傅里叶变换、短时傅里叶变换、小波变换、小波包变换和希尔伯特-黄变换阶段[15, 71-75]。

在上述信号分析方法中, 傅里叶变换和短时傅里叶变换隐含了信号分解为无限长正弦信号叠加的条件, 而小波变换、小波包变换属于多尺度分析方法, 在信号的高频处时间细分、低频处频率细分, 能自动适应时频信号分析的要求, 且对分解得到的成分没有强制规定频率的类型。因此小波变换仍是目前非平稳态信号分析的最有效方法之一。但小波变换要求小波窗内信号必须平稳, 小波基的有限长又会造成信号能量泄漏, 同时小波函数具有多样性。无论是傅里叶变换还是小波变换都是用一种固定的基或核函数来对信号进行分解, 均受到海森堡测不准原理的限制, 希尔伯特-黄变换(Hilbert-Huang transform, HHT)这类自适应分解算法也被更多学者关注[76]。

3.2 水下爆炸声信号时域特性

炸药水下爆炸冲击波的水声特性与冲击波峰值压力、正压持续时间和能流密度等特征相关。这些特征是信号在时域中的投影, 能较为直观地体现声信号的性能, 也为频谱分析提供了依据。

Blaik等[19]分析了6 706 m深度以内的小药量(最小20 g于4 145 m深爆炸)水下爆炸试验数据与Arons[18]总结得到的冲击波峰值经验公式, 认为冲击波峰值超压不受爆炸深度的影响, 但正压作用时间随爆炸深度的增加而减小, 导致冲击波声辐射能减少。Goertner[77]研究了冲击波压力的影响因素, 分析了不同介质声速和密度对其的影响。Geoff等[78]对小当量炸药爆炸声压级测量进行了研究, 得出了风速、温度等气象条件与爆炸声压级的拟合关系并得出计算公式。Alexander等[79]在距离维吉尼亚海岸7 km外进行了水下爆炸峰值压力和声压级的测量, 并将试验测量得到的峰值压力与半经验公式计算结果相比较, 给出了浅海环境下利用能流密度计算水下爆炸声压级的半经验公式。

吴成等[80-81]对比了TNT、RS211和RS3-4等3种炸药等体积爆炸条件下在不同距离处的冲击波声压级L及其高于背景噪声声压级的持续时间, 如图7所示。潘正伟等[82]对RDX、TNT、8701等炸药进行了小药量爆炸试验, 测得的等效声源级均在210 dB以上,炸药质量、爆距与等效声源级之间满足水下爆炸相似律。

图7 不同位置处3种炸药声压级时程曲线

在浅海环境下, 实际测得的水下爆炸声信号往往受各类散射元或等效散射元的影响, 不再是纯净的冲击波和气泡脉冲信号, 而是如图8所示的混响信号(图中, Δ表示超压, 即总压力与环境静水压力的差值), 这种混响效应能够增加水下爆炸声信号的持续脉宽。

图8 实测混响信号声压随时间变化曲线

Vadov[83]和Mikryukov等[84]研究了从深海到近海水下爆炸声波的远程传播, 并在2种深度上对距爆源80～120 km的声混响信号进行了观测分析。Hines等[85]在浅海进行了试验, 得到频率分别为21、28和36 kHz的混响信号, 并与通用声呐模型的计算结果进行了对比, 对混响曲线中极值点的形成机理进行了研究。Stanic 等[86]在巴拿马城进行了试验, 得到了高频信号双基地混响, 经过分析可知混响强度随着掠射角的减小而减小。Guzhaniva等[87]在浅海进行了试验, 近似估计了40～400 Hz信号的吸收系数和反射系数。Li等[88]分析了2001年ASIAEX项目的试验数据, 发现延迟一段时间的双基地混响曲线和单基地混响曲线是近似的。

3.3 水下爆炸声信号频谱特性

水下爆炸能量分布在很宽的频率范围内。基于此特点, 许多领域都将水下爆炸作为声源, 为了更好地描述声信号的特性, 需要获取其在频率上的分布。水下爆炸声信号的频谱特性反映了信号所含分量的幅度、相位随频率的分布情况。

3.3.1 能流密度谱级

潘正伟等[82]指出水声设备一般都具备抗干扰能力, 如在电子线路中设置积分电路。因此早期对水下爆炸声信号频谱特性研究时往往分析的是信号的能流密度谱级而不是实时的声压谱级。

早期实测水下爆炸声信号处理时一般采用倍频程滤波的方式获得信号的频带特性。Weston[89]将25～6 400 Hz之间的频段划分为8个倍频程, 利用倍频程对不同质量炸药水下爆炸信号进行滤波, 获得了对应频程的能流通量, 并将该能流通量除以带宽以获得绝对自由场能流谱级。随后, Weston在对水下爆炸信号进行频谱分析的基础上, 提出可将各种频谱等效为1 lb炸药的谱, 理论曲线与不同质量炸药缩放结果如图9所示(图中,()表示绝对能流谱级, 其中理论曲线为频谱级, 试验点为1/3倍频程滤波后的频带级,为频率)。

图9 归一化至1 lb炸药的绝对能流谱级随频率变化曲线

在水下爆炸半经验公式的基础上, Raitt、Weston[89]等采用傅里叶变换对Arons等[18, 90-91]拟合得到的冲击波、气泡脉冲半经验公式分别进行了处理, 将时域关系投影到频域中获得了能流密度谱, 并分析了炸药质量和爆炸深度对能流密度谱的影响。Christian等[92]发现Weston导出的能流密度谱在气泡脉冲基频(第1次气泡脉动周期的倒数)处具有明显的峰值, 该峰值随着爆炸深度的增加以及炸药质量的减少而增加。随后, Christian[93]分离了水平距离与深度的影响, 利用气泡脉动基频和炸药质量将频率和能流密度归一化, 获得了适用于深水爆炸条件下的能流密度谱。Kibblewhite等[94]通过不同炸药质量、起爆深度的试验结果证明了Christian能流密度谱的正确性。张翠平[95]从傅里叶变换出发推导了水下爆炸能量谱密度关系, 并根据量纲分析导出了水下爆炸频率特性相似关系与能量谱密度相似关系。

江国进等[96]采用HHT方法对水下爆炸声信号进行处理, 通过球面扩展修正和1/3倍频程频带化的方式得到了Hilbert能量谱, 并与傅里叶能流密度谱进行了对比, 两者所表示的频带声源级E(0)如图10所示。从图中可看出, 经过1/3倍频程平均后, 傅里叶能流密度谱和Hilbert能量谱较为接近。

图10 基于Hilbert能量谱与Fourier能流密度谱的1/3倍频程频带声源级曲线

3.3.2 水下爆炸声压谱级及能量分布

随着数字信号处理技术的快速发展, 研究者开始借助FFT算法、多尺度分析方法及自适应分解算法等信号分析工具对水下爆炸声信号的谱特征进行提取。

潘正伟等[82]用FFT将不同药量、不同距离处测得的RDX炸药水下爆炸冲击波压力信号从时域变换到频域获得了冲击波信号的傅里叶谱, 结果表明冲击波信号的频率成分极为丰富。吴成等[81, 97]借助Welch方法提取了兆帕级水下爆炸冲击波原始信号和小波分层信号的功率谱, 发现TNT、RS211、RS3-4这3种炸药的功率随频率变化的特性在远场时差别不大, 且10 kHz以下的信号能量占比较大。

贾虎等[98-99]计算了纤维爆炸索水下爆炸冲击波信号的功率谱, 并分别利用小波变换和基于经验模态分解(empirical mode decomposition, EMD)算法的HHT对冲击波信号进行了特征提取, 讨论了水下爆炸冲击波信号在各层小波频段上的能量分布状况。范志强等[100]利用小波变换方法对纤维爆炸索水下连续脉冲爆炸信号进行了时频特性分析, 认为每个脉冲冲击波主要分布在125 kHz以下。

盛振新、裴善报等[15, 74, 101-104]采用小波变换和HHT分别对850 m处、6 200 m处测得的水下单药包爆炸冲击波信号、单药包爆炸声信号和连续爆炸声信号进行了分解, 计算了信号的功率谱、能量分布状况、Hilbert谱和边际谱, 并研究了起爆间隔时间对连续爆炸声信号的影响。结果显示: 单药包情况下, 声信号的能量主要分布频带相对于冲击波信号更低; 不同起爆间隔时间下, 连续爆炸声信号的功率谱和能量分布状况相差不大, 能量分布情况与单药包爆炸声信号类似, 但会有部分能量从低频向高频转移。

易流[105]针对不同水深条件下的爆炸冲击波试验数据用2种小波基函数进行了分解, 证明了水下爆炸冲击波压力信号对小波基函数的选择不敏感。孙钟阜等[106]基于HHT法对水下单药包爆炸试验数据进行处理, 得到了水下爆炸声信号的Hilbert谱, 同时根据声速剖面计算了声线轨迹, 发现能量谱中的局部极值点是由声线轨迹和海底相互作用导致的。

4 水下爆炸声源应用

水下爆炸声学效应的研究表明, 水下爆炸产生的强噪声源除了具有高声功率、宽频率及无指向性等优点外, 还可以很方便地投掷到指定的任意深度上爆炸, 成本低、经济性好。因此, 水下爆炸声源在海洋资源探测、水文环境反演、水下微小隐身目标探测和水声对抗干扰等领域有着广泛的应用前景。

4.1 目标探测与定位

水面舰艇编队是水下攻防的重要力量, 在与水下威胁目标的对抗中, 面临的首要困难在于难以远程发现和准确识别水下威胁目标。通过爆炸声源产生高强度低频爆炸声信号, 并利用异地舰载声呐接收目标回波的方式可有效解决上述问题, 完成对目标的快速检测与定位。

刘琳等[107]针对拖曳阵声呐采用主动工作模式时水面舰艇易于过早暴露、遭受攻击的问题, 提出了一种基于爆炸声源的多基地远程探测新技术, 该技术通过爆炸声源产生高强度低频爆炸声信号, 利用大孔径低频拖曳线列阵声呐进行高增益接收, 结合对潜艇回波与直达波的参数提取与处理, 同步完成对潜艇目标的快速检测与定位。

黄聪等[108]基于双基地声呐定位原理和均匀水声环境假设, 结合爆炸声源在基线延长线附近一定开角范围内具有探测优势的特点, 提出了在以声呐为圆心的圆周上配置多枚爆炸声源的方式扩大探测覆盖角度, 实现在大开角范围内的舰船警戒, 多爆炸声源布置如图11所示(图中显示了7个均匀布置的爆炸声源, 分别位于距离接收声呐的半径为80 km、开角范围为15°～165°的圆弧上, 图中坐标轴表示的、均为空间坐标)。

图11 爆炸声源距接收平台80 km的探测曲线

张朝金等[109]提出了一种基于半经验公式与匹配场联合处理的单阵元爆炸声源快速定位方法。该方法在匹配场定位的基础上, 根据冲击波峰值和气泡脉动周期测量值、水下爆炸半经验公式与多途时延差建立代价函数, 实现了用单阵元在近距离爆炸声源的深度和距离精确反演。该方法指出, 一次气泡脉动周期与多途时延差的联合匹配可提高对爆炸声源深度的估计精度, 且冲击波峰值与多途时延差的联合匹配可提高对距离的估计精度。

4.2 水声对抗

水下爆炸噪声不仅声源级高, 而且频带宽, 特别在低频段具有很强的声功率, 是良好的水下声干扰源, 不仅能对在高频声频带工作的鱼雷自导系统实施干扰, 而且能对在低频工作的声呐实施干扰。水下爆炸产生的声信号从几十赫兹到 50 kHz以上都有相当强的声功率, 可完全覆盖目前世界上鱼雷声自导系统的各个工作频段, 使鱼雷声自导系统产生侦听饱和、阻塞抑制, 使自导跟踪失去目标接触。

李继民[110]用水下连续爆炸声信号分别对某型号国产鱼雷和从国外引进的A244/S型鱼雷进行对抗试验。试验结果表明, 无指向性的水下连续爆炸声信号能够使鱼雷丢失目标并不断重新搜索目标。特别地, 当水下爆炸出现在鱼雷和目标之间时, 声自导鱼雷即使是现代智能化的自导鱼雷也难以在此噪声背景下区分出有效信号, 更无法对目标回波信号的前后沿陡度、形状和距离进行逻辑判别。

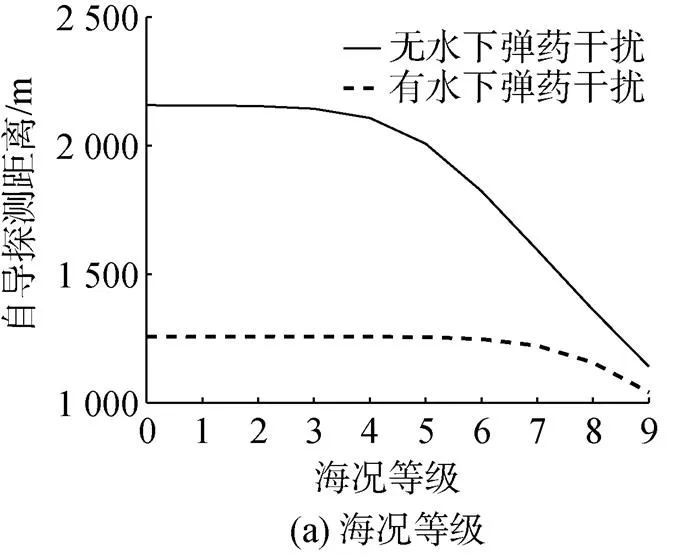
曾星星[111]、裴善报[74]以主动声制导鱼雷自导探测距离平均下降率为水下爆炸声干扰弹对抗效果的评价指标, 建立了鱼雷自导探测模型, 并分别对不同海况、鱼雷航行深度、干扰弹装药量等因素影响下的鱼雷自导探测距离进行了仿真, 结果如图12所示。仿真结果表明水下爆炸声干扰弹产生的噪声信号能够对主动声呐起到很好的干扰效果, 尤其是在海况好、航深大的情况下自导探测距离下降率能够接近50%。

鉴于单个水下爆炸药包难以形成长持续时间的低频辐射压力信号, Kedrinskii[112]在其著作中引述了几种索式水下爆炸声源, 通过给定时间间隔单独或连续地起爆, 在水中产生了一系列脉冲式冲击波和强混响声。其中一种爆炸声源将一系列高爆炸药包按照链式垂直排列, 另一种爆炸声源将炸药制成爆炸索并螺旋缠绕。螺旋缠绕爆炸索产生的典型信号如图13所示。盛振新[15]、裴善报[74]将10个爆炸单元用缆绳串联后设定一定的时间间隔连续起爆, 同样形成了类似于图13所示的连续脉冲信号, 有效干扰时间可达秒级。

图13 扁平螺旋装药水下爆炸时的水声信号

4.3 海洋预报

全球业务化海洋预报系统以海洋动力数值模式作为动力框架, 将近实时高质量的观测场通过资料同化输入到模式中, 实现对全球范围多时空尺度海洋状况的预报。海洋环境的参数反演是海洋预报环节中不可缺少的重要步骤。

海底声学参数如海底密度、声速和声衰减等是利用声学研究海底的重要指标, 与海底物理特性有着密切的关系。对海底直接取样, 价格昂贵, 速度慢, 且只能提供离散点的信息, 而通过信噪比较高的爆炸声回波反演海底声学参数可以消除海底直接取样所面临的大部分问题, 越来越受到人们的关注。海底声学参数反演试验布置一般如图14所示。

图14 海底参数反演试验示意图

商德江等[113]在中国北海海区使用手榴弹作为爆炸声源进行了海底参数反演试验, 反演过程中, 根据本地混响试验时所投的爆炸声信号的直达波和海底反射波的功率谱得到不同频率下的垂直反射系数幅值, 结合Hamilton经验公式反演了海底的声速和密度。

周鸿涛等[114]利用2014年在南中国海开展的定深爆炸声信号数据进行海底地声参数反演, 反演过程中考虑到不同海底声参数对不同声场物理参数的敏感程度不同、不同海底声参数对不同反演方法的敏感程度亦不同的特征, 综合应用了3种不同反演方法得到了海底声阻抗、沉积物声速、沉积物密度和海底沉积层厚度等地质声参数。

徐东等[115]考虑到爆炸声源的二次脉动时间只与爆炸深度和炸药当量有关, 利用滤去二次脉动和海面反射信号的爆炸声, 结合射线模型反演了沉积层的声速和厚度, 并根据Hamilton经验公式计算得到了沉积层密度。

5 展望

综上所述, 在工程界和学术界, 国内外学者对水下爆炸及其声学效应进行了大量的理论、试验研究和探索, 尽管相关研究取得了重要进展, 但在诸多方面仍然面临新的挑战, 水下爆炸声源技术的研究工作在以下几个方面仍有待于加强, 主要包括:

1) 水下爆炸声源的能量输出特性与典型炸药材料尤其是新型高能非理想含铝炸药的装药结构、起爆状态的量化关系尚不明确, 从水下爆炸动力学理论和波动理论等方面深入阐述高能炸药材料水下爆炸的能量转换机制和致声机理方面的研究较为缺乏;

2) 对于水下爆炸声混响效应的评估和表征多依赖于水下爆炸试验方法, 缺乏综合考虑爆炸声信号时空特性和水域界面效应的水下爆炸声混响强度预报表征方法。HHT等信号分析方法在水下爆炸的应用愈发广泛, 但仍存在包络定义、模态混叠现象等许多问题, 需要研究适合水下爆炸声的宽带非平稳信号分析方法;

3)阵列式水下多脉冲爆炸强噪声源的致声机理及工程应用尚处于探索研究阶段, 对于水下多脉冲爆炸声混响效应的表征评估及应用有待于进一步拓展, 多脉冲爆炸单元在不同空间阵列散布形式、不同水下爆炸界面的声学特性以及多个装药爆炸产生的冲击波之间相互作用规律方面的研究尚不完善。

[1] Urick R J. Principles of Underwater Sound for Engineers[M]. New York: McGraw-Hill Press, 1967.

[2] Arons A B, Yennie D R. Energy Partition in Underwater Explosion Phenomena[J]. Review of Modern Physics, 1948, 20(3): 519-536.

[3] 李宁, 陈建峰, 黄建国, 等. 各种水下声源的发声机理及其特性[J]. 应用声学, 2009, 28(4): 241-248.

Li Ning, Chen Jian-feng, Huang Jian-guo, et al. Sounding Mechanisms and Characteristics of Various Underwater Sound Sources[J]. Applied Acoustics, 2009, 28(4): 241- 248.

[4] 卢苇. 大功率甚低频水下声源研究[D]. 哈尔滨: 哈尔滨工程大学, 2011.

[5] 宁建国,王成,马天宝. 爆炸与冲击动力学[M]. 北京:国防工业出版社, 2010.

[6] 罗斯 D. 水下噪声原理[M]. 《水下噪声原理》翻译组, 译. 北京: 海洋出版社, 1983.

[7] Lighthill M J. On Sound Generated Aerodynamically I. General Theory[J]. Proceedings of the Royal Society of London Series A, 1952, 211(1107): 564-587.

[8] Tam C K W. Computational Aeroacoustics Examples Showing the Failure of the Acoustic Analogy Theory to Identify the Correct Noise Sources[J]. Journal of Computational Acoustics, 2002, 10(4): 387-405.

[9] Kirkwood.J.G, Bethe.H. The Pressure Wave Produced by an Underwater Explosion Part I: OSRD 588[R]. [S.l]: Office of Scientific Research and Development , 1942.

[10] Kirkwood J G, Brinkley S R. Theory of the Propagation of Shock Waves from Explosive Sources in Air and Water: OSRD 4818 [R]. [S.l.]: Office of Scientific Research and Development, 1945.

[11] Kedrinskii V K. Kirkwood-Bethe Approximation for an Underwater Explosion with Cylindrical Symmetry[J]. Comb- ustion Explosion & Shock Waves, 1972, 8(1): 94-100.

[12] Geers T L, Hunter K S. An Integrated Wave-effects Model for an Underwater Explosion Bubble[J]. The Journal of the Acoustical Society of America, 2002, 111(4): 1584-1601.

[13] 李澎, 徐更光.水下爆炸冲击波传播的近似计算[J]. 火炸药学报, 2006, 29(4): 21-24.

Li Peng, Xu Geng-guang. Approximate Calculation of Underwater Explosion Shock Wave Propagation[J]. Chinese Journal of Explosives & Propellants, 2006, 29(4): 21-24.

[14] Wang S S, Gui Q Y, Zhang J X, et al. Theoretical and Experimental Study of Bubble Dynamics in Underwater Explosions[J]. Phys. Fluids, 2021, 33: 126113.

[15] 盛振新. 水下连续爆炸声学特性及信号分析研究[D]. 南京: 南京理工大学, 2013.

[16] Weston D E. The Low-frequency Scaling Laws and Source Levels for Underground Explosions and Other Disturbances[J]. Geophysical Journal of the Royal Ast- ronomical Society, 1960, 3(2): 191-201.

[17] Cole R H. Underwater Explosion[M]. New Jersey: Princeton University Press, 1948.

[18] Arons A B. Underwater Explosion Shock Wave Parameters at Large Distances from the Charge[J]. Journal of the Acoustical Society of America, 1954, 26(3): 343-346.

[19] Blaik M, Christian E A. Near-Surface Measurements of Deep Explosions I. Pressure Pulses from Small Charges[J]. Journal of the Acoustical Society of America, 1965, 38(1): 50-56.

[20] Alpaslan T, Serdar B. Blast Pressure Measurements of an Underwater Detonation in the Sea[J]. Journal of Marine Science and Application, 2021(2): 706-713.

[21] Temkin S. Review of the Propagation of Pressure Pulses Produced by Small Underwater Explosive Charges: AD-A194642[R/OL].[2022-05-26]. https://apps.dtic.mil/st i/pdfs/ ADA194642.pdf, 1988.

[22] DuMond J W M, Cohen E R, Panofsky E K H, et al. A Determination of the Wave Forms and Laws of Propagation and Dissipation of Ballistic Shock Waves[J]. The Journal of the Acoustical Society of America, 1946, 18(1): 97-118.

[23] Landau L D, Lifshitz E M. Fluid Mechanics[M]. New York: Pergamon Press, 1959.

[24] Wright W M. Propagation in Air of N Waves Produced by Sparks[J]. The Journal of the Acoustical Society of America, 1983, 73(6): 1948-1955.

[25] Temkin S, Maxham D. Nonlinear Lengthening of a Triangular Acoustic Pulse[J]. Physics of Fluids, 1985, 28(10): 3013-3017.

[26] 肖川, 宋浦, 梁安定. 炸药水中爆炸规律的研究进展[J]. 火炸药学报, 2006, 29(6): 19-22, 26.

Xiao Chuan, Song Pu, Liang An-ding. Research Development of Underwater Explosion Mechanism[J]. Chinese Journal of Explosives & Propellants, 2006, 29(6): 19-22, 26.

[27] 张岩, 李风华, 李整林, 等. 爆炸信号中气泡脉动去除方法及其应用[J]. 声学学报, 2009, 34(2): 124-130.

Zhang Yan, Li Feng-hua, Li Zheng-lin, et al. The Method of Bubble Pulse Removal from Explosive Signals and Its Application[J]. Acta Acustica, 2009, 34(2): 124-130.

[28] 林京. 爆炸声信号二次脉动的剔除与简正波提取[C]//中国声学学会2005年青年学术会议. 杭州: 中国声学学会, 2005.

[29] 朱业, 张仁和. 负跃层浅海中的脉冲声传播[J]. 中国科学: 数学物理学天文学技术科学, 1996(3): 271-279.

Zhu Ye, Zhang Ren-he. Pulse Propagation in Negative Thermocline Shallow Water Environment[J]. Science in China, Sea .A, 1996(3): 271-279.

[30] 史洺宇, 齐梅, 易成高, 等. 静水中气泡上升运动及阻力系数研究[J]. 计算力学学报, 2019, 36(3): 422-428.

Shi Ming-yu, Qi Mei, Yi Cheng-gao, et al. Study on Kinetic Properties and Drag Coefficient of Rising Bubble Behavior in Still Water[J]. Chinese Journal of Computational Mechanics, 2019, 36(3): 422-428.

[31] 徐贞, 张迪, 陈时, 等. 黏性对含气泡液体中声波传播的影响[J]. 中国科学: 物理学力学天文学, 2018, 48(4): 48-56.

Xu Zhen, Zhang Di, Chen Shi, et al. Effect of Viscosity on Propagation Properties of Acoustic Waves in Liquids with Bubbles[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2018, 48(4): 48-56.

[32] 程广利, 罗夏云, 孟路稳, 等. 消声水池中水射流噪声特性试验研究[J]. 兵工学报, 2018, 39(6): 1165-1170.

Cheng Guang-li, Luo Xia-yun, Meng Lu-wen, et al. Experimental Investigation into Noise Characteristics of Water Jet in Anechoic Tank[J]. Acta Armamentarii, 2018, 39(6): 1165-1170.

[33] 周远, 罗二仓. 热声热机技术的研究进展[J]. 机械工程学报, 2009, 45(3): 20-32.

Zhou Yuan, Luo Er-cang. Advance in Thermoacoustic Technology[J]. Chinese Journal of Mechanical Engineering, 2009, 45(3): 20-32.

[34] 李捷. 烟火药水下燃烧气泡运动特征及声源装药技术[D]. 南京: 南京理工大学, 2016.

[35] Besant W H. Hydrostatics and Hydrodynamics[M]. London: Cambridge University Press, 1859.

[36] Rayleigh L. On the Pressure Developed in a Liquid During the Collapse of a Spherical Cavity[J]. Phil. Mag, 1917, 34: 94-98.

[37] Plesset M S. The Dynamics of Cavitation Bubbles[J]. Journal of Applied Mechanics, 1949, 16: 227-282.

[38] Poritsky H. The Collapse or Growth of a Spherical Bubble or Cavity in a Viscous Fluid[J]. Journal of Applied Mechanics Transactions of the Asme, 1951, 18(3): 332- 333.

[39] Noltingk B E, Neppiras E A. Cavitation Produced by Ultrasonics[J]. Proceedings of the Physical Society B, 1950, 63(9): 674-685.

[40] Noltingk B E, Neppiras E A. Cavitation Produced by Ultrasonics: Theoretical Conditions for the Onset of Cavitation[J]. Proceedings of the Physical Society B, 1951, 64(12): 1032-1038.

[41] Lauterborn W. Numerical Investigation of Nonlinear Oscillations of Gas Bubbles in Liquids[J]. Journal of the Acoustical Society of America, 1976, 59(2): 283-293.

[42] 刘孟庵.水声工程[M]. 浙江: 浙江科学技术出版社, 2002.

[43] Etter P C. Underwater Acoustic Modeling and Simulation[M]. 3rd, ed. London, UK: Spon Press(Tay & Francis Group), 2003.

[44] Abawi A T, Kuperman W A, Collins M D. The Coupled Mode Parabolic Equation[J]. The Journal of the Acoustical Society of America, 1996, 100(4): 2613-2614.

[45] 彭朝晖, 张仁和. 三维耦合简正波-抛物方程理论及算法研究[J]. 声学学报, 2005, 30(2): 97-102.

Peng Zhao-hui, Zhang Ren-he. On Study of the Theory and Algorithm of the Three Dimensional Coupled Mode-Para- bolic Equation[J]. Acta Acustica, 2005, 30(2): 97-102.

[46] 秦继兴, Katsnelson Boris, 彭朝晖, 等. 三维绝热简正波-抛物方程理论及应用[J]. 物理学报, 2016, 65(3): 144-152.

Qin Ji-xing, Katsnelson Boris, Peng Zhao-hui, et al. Three-Dimensional Adiabatic Mode Parabolic Equation Method and Its Applications[J]. Acta Physica Sinica, 2016, 65(3): 144-152.

[47] Paul C, Etter. Advanced Applications for Underwater Acoustic Modeling[EB/OL].(2012-5-8)[2022-04-02]. Htt- ps: //xueshu.baidu. com/usercenter/paper/show? paperid= ec62729644b73d88dbe102f60e8de80f&site=xueshu_se.

[48] Porter M B. The Bellhop Manual and User’s Guide: Preliminary Draft. Heat, Light, and Sound Research[M]. Inc. La Jolla, CA, USA, 2011.

[49] Gul S, Zaidi S, Khan R, et al. Underwater Acoustic Channel Modeling Using BELLHOP Ray Tracing Method[C]//International Bhurban Conference on Applied Sciences & Technology. Islamabad, Pakistan: IEEE, 2017: 665-670.

[50] 吴丽丽, 彭朝晖. 西太平洋远程脉冲声传播实验数据分析[J]. 中国科学: 物理学力学天文学, 2016, 46(9): 8-15.

Wu Li-li, Peng Zhao-hui. Analysis of Long-range Sound Propagation in West Pacific Ocean[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2016, 46(9): 8-15.

[51] Pekeris C L. Theory of Propagation of Explosive Sound in Shallow Water[M/OL]. [S.l.]. Geological Society of America, 1948[2022-4-5]. https://pubs.geoscienceworld. org/gsa/books/book/33/chapter/3786458/THEORY-OF-PROPAGATION-OF-EXPLOSIVE-SOUND-IN?redirectedFrom=PDF.

[52] Pierce A D. Extension of the Method of Normal Modes to Sound Propagation in an Almost-Stratified Medium[J]. Journal of the Acoustical Society of America, 1965, 37(1): 19-27.

[53] Evans R B. A Coupled Mode Solution for Acoustic Propagation in a Waveguide with Stepwise Depth Variations of a Penetrable Bottom[J]. The Journal of the Acoustical Society of America, 1983, 74(1): 188-195.

[54] Porter M, Reiss E L. A Numerical Method for Ocean- acoustic Normal Modes[J]. The Journal of the Acoustical Society of America, 1984, 76(1): 244-252.

[55] 张仁和.水下声道中的平滑平均声场[J]. 声学学报, 1979(2): 102-108.

Zhang Ren-he. Smooth-Averaged Sound Field in Underwater Sound Channel[J].Acta Acoustic, 1979(2): 102- 108.

[56] 张仁和, 李风华. 浅海声传播的波束位移射线简正波理论[J]. 中国科学(A辑), 1999, 29(3): 241-251.

Zhang Ren-he, Li Feng-hua. BDRM Theory of Shallow Sea Acoustic Propagation[J]. Science in China(Seriesa A), 1999, 29(3): 241-251.

[57] 曹亮, 韩引海, 谢辉. 定深爆炸声源声信号能量分配试验研究[J]. 声学技术, 2020, 39(1): 45-48.

Cao Liang, Han Yin-hai, Xie Hui. Experimental Study on the Sound Energy Distribution of the Depth-Detonating Explosion Source[J]. Technical Acoustics, 2020, 39(1): 45-48.

[58] Bucker H P, Morris H E. Normal-Mode Reverberation in Channels or Ducts[J]. Journal of the Acoustical Society of America, 1968, 44(3): 827-829.

[59] 吴承义. 用射线方法计算浅海混响平均强度(I)[J]. 声学学报, 1979, 4(2): 114-119.

Wu Cheng-yi. Calculation of the Mean Intensity of Shallow Sea Reverberation by the Ray Method(I)[J]. Acta Acustica, 1979, 4(2): 114-119.

[60] 张仁和, 金国亮.浅海平均混响强度的简正波理论[J].声学学报, 1984, 9(1): 12-20.

Zhang Ren-he, Jin Guo-liang. Mode Theory of Shallow Sea Mean Reverberation Intensity[J]. Acta Acustica, 1984, 9(1): 12-20.

[61] Ellis D D, Crowe D V. Bistatic Reverberation Calculations Using a Three-dimensional Scattering Function[J]. The Journal of the Acoustical Society of America, 1991, 89(5): 2207-2214.

[62] Cable P G, Yudichak T W, Dorfman Y, et al. On Shallow-Water Bottom Reverberation Frequency Dependency[J]. IEEE Journal of Oceanic Engineering, 2006, 31(1): 145-155.

[63] 惠娟, 惠俊英, 王自娟.收、发分置混响平均强度理论预报[J]. 声学学报, 2009, 34(1): 47-53.

Hui Juan, Hui Jun-ying, Wang Zi-juan. The Prediction of Bistatic Reverberation Average Strength[J]. Acta Acistica, 2009, 34(1): 47-53.

[64] 惠娟, 王自娟, 惠俊英, 等.双基地混响平均强度理论及仿真预报[J]. 物理学报, 2009, 58(8): 5492-5499.

Hui Juan, Wang Zi-juan, Hui Jun-ying, et al. The Theoretical and Simulation Prediction of Bistatic Reverberation Average Strength[J]. Acta Physica Sinica, 2009, 58(8): 5492-5499.

[65] 盛振新, 刘荣忠, 郭锐.一种改进的水下爆炸声混响模型[J]. 声学学报, 2012, 37(5): 484-488.

Sheng Zhen-xing, Liu Rong-zhong, Guo Rui. An Advanced Reverberation Model of Underwater Explosive Sound[J]. Acta Acustica, 2012, 37(5): 484-488.

[66] Guo R, Lei L, Sheng Z X, et al. A Three-dimensional Bistatic Reverberation Model of Underwater Explosion by Interface Scattering at Variable Sound Speeds[J]. Journal of Low Frequency Noise Vibration and Active Control, 2019, 38(2): 427-440.

[67] 欧阳的华, 潘功配, 关华, 等. 具有脉动燃烧效应的烟火药水中燃烧声频特性[J]. 含能材料, 2008, 16(5): 603- 605.

Ouyang Di-hua, Pan Gong-pei, Guan Hua, et al. Experimental Study on Acoustic Frequency Property of Pulsating Combustion Underwater for Pyrotechnic Composition[J]. Chinese Journal of Energetic Materials, 2008, 16(5): 603-605.

[68] 陈颙, 王宝善. 用气枪震源研究大陆浅部的地下结构及其变化[C]//2016中国地球科学联合学术年会论文集(二十五). 北京: 中国科学技术大学, 2016.

[69] 温华兵, 张健, 尹群, 等. 水下爆炸船舱冲击响应时频特征的小波包分析[J]. 工程力学, 2008, 25(6): 199- 203.

Wen Hua-bing, Zhang Jian, Yin Qun, et al. Wavelet Packet Analysis of Time-Frequency Characteristic of Cabin Shock Respinse Due to Underwater Explosion[J]. Engineering Mechanics, 2008, 25(6): 199-203.

[70] 李夕兵, 张义平, 刘志祥, 等. 爆破震动信号的小波分析与HHT变换[J]. 爆炸与冲击, 2005, 25(6): 528- 535.

Li Xi-bing, Zhang Yi-ping, Liu Zhi-xiang, et al. Wavelet Analysis and Hilbert-Huang Transform of Blasting Vibration Signal[J]. Explosion and Shock Waves, 2005, 25(6): 528-535.

[71] 杜志鹏, 汪玉, 杨洋, 等. 舰艇水下爆炸冲击信号拟合及应用[J]. 振动与冲击, 2010, 29(3): 182-184.

Du Zhi-peng, Wang Yu, Yang Yang, et al. Curve Fit Method for Naval Underwater Explosion Shock Signal and Its Application[J]. Journal of Vibration and Shock, 2010, 29(3): 182-184.

[72] 晏俊伟, 龙源, 方向, 等. 基于小波包变换的爆破地震波时频特征提取及分析[J]. 振动与冲击, 2007, 26(4): 25-29.

Yan Jun-wei, Long Yuan, Fang Xiang, et al. Time-Fre- quency Characteristics Extracting and Analysis of Blasting Seismic Wave Based on Wavelet Packet Transformation[J]. Explosion and Shock Waves, 2007, 26(4): 25- 29.

[73] 贾虎. 纤维爆炸索水下爆炸特性与应用研究[D]. 合肥: 中国科学技术大学, 2011.

[74] 裴善报. 水下连续爆炸声干扰器相关技术研究[D]. 南京: 南京理工大学, 2015.

[75] 有悦. 深水爆炸压力时频特性分析方法研究与应用[D]. 武汉: 武汉科技大学, 2021.

[76] 彭思龙, 李保滨, 胡晰远. 小波与滤波器组设计: 理论及其应用[M]. 北京: 清华大学出版社, 2017.

[77] Goertner J F. Scaling Underwater Explosion Shock Waves for Differences in Ambient Sound Speed and Density: AD-A102365[R/OL]. [2022-05-26]. https://apps.dtic.mil/ sti/ pdfs/ ADA102365.pdf.

[78] Geoff K, David J S, Alan G S. The Use of Meteorological Profiles to Predict the Peak Sound-Pressure Level at Distance from Small Explosions[J]. Journal of the Acoustical Society of America, 1987, 81(4): 888-896.

[79] Alexander G S, Peter H D. Peak Sound Pressure and Sound Exposure Level from Underwater Explosions in Shallow Water[J]. The Journal of the Acoustical Society of America, 2014, 136(3): 218-223.

[80] 吴成, 廖莎莎, 李华新, 等. 水下爆炸的一些声学特性分析[J]. 北京理工大学学报, 2008, 28(8): 719-722.

Wu Cheng, Liao Sha-sha, Li Hua-xin, et al. Analysis of Acoustic Characteristics for HE Charge Underwater Explosion[J]. Transactions of Beijing Institute of Technology, 2008, 28(8): 719-722.

[81] 吴成, 廖莎莎, 李华新, 等. 3种炸药水下爆炸的声波特性测试及其对比分析[J]. 北京理工大学学报, 2009, 29(1): 1-4.

Wu Cheng, Liao Sha-sha, Li Hua-xin, et al. An Investigation and Analysis on the Acoustic Characteristics of Three Types of Explosive Charges by Underwater Explosion[J]. Transactions of Beijing Institute of Technology, 2009, 29(1): 1-4.

[82] 潘正伟, 焦善武.弹药水中爆炸的水声效应[J]. 弹箭与制导学报, 1998(3): 39-43.

Pan Zheng-wei, Jiao Shan-wu. Underwater Acoustic Effect of Ammunition Explosion in Water[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 1998(3): 39-43.

[83] Vadov R V. Time Structure of Bistatic Reverberation in the Long-Range Propagation of Explosion-Generated Signals[J]. Acoustical Physics, 2007, 53(2): 172-180.

[84] Mikryukov A V, Popov O E. The Effect of Geoacoustic Characteristics of the Bottom on the Long-range Sound Propagation in an Inhomogeneous Ocean[J]. Acoustical Physics, 2006, 52(4): 435-439.

[85] Hines P C, Ellis D D. High-frequency Reverberation in Shallow Water[J]. IEEE Journal of Oceanic Engineering, 1997, 22(2): 292-298.

[86] Stanic S, Kennedy E, Ray R I. High-frequency Bistatic Reverberation from a Smooth Bottom[J]. J. Acoust. Soc. Am, 1993, 93(5): 2633-2638.

[87] Guzhavina D V, Gulin E P. Experimental Study of Low-frequency Bistatic Reverberation in Shallow Water[J]. Acoustical Physics, 2000, 46(6): 664-669.

[88] Li F H, Liu J J. Bistatic Reverberation in Shallow Water: Modeling and Data Comparison[J]. Chin.Phys.Lett, 2002, 19(8): 1128-1130.

[89] Weston D E. Underwater Explosions as Acoustic Sou- rces[J]. Proc. Phys. Soc., 1960, 76(2): 233-249.

[90] Arons B A, Slifko J P, Carte A. Secondary Pressure Pulses Due to Gas Globe Oscillation in Underwater Explosions. I. Experimental Data[J]. Journal of the Acoustical Society of America, 1948, 20(3): 271-276.

[91] Arons A B. Secondary Pressure Pulses Due to Gas Globe Oscillation in Underwater Explosions. II. Selection of Adiabatic Parameters in the Theory of Oscillation[J]. Journal of the Acoustical Society of America, 1948, 20(3): 271-276.

[92] Christian E A, Blaik M. Near-Surface Measurements of Deep Explosions II. Energy Spectra of Small Charges[J]. Journal of the Acoustical Society of America, 1965, 38 (1): 57-62.

[93] Christian E A. Source Levels for Deep Underwater Explosions[J]. The Journal of the Acoustical Society of America, 1967, 42(4): 187-214.

[94] Kibblewhite A C, Denham R N . Measurements of Acoustic Energy from Underwater Explosions[J]. The Journal of the Acoustical Society of America, 1970, 48(1B): 346-351.

[95] 张翠平. 水下延时爆炸声信号的模拟[D]. 南京: 南京理工大学, 2006.

[96] 江国进, 曹亮. 基于HHT方法的水下爆炸声信号时频特性分析[J]. 舰船电子工程, 2020, 40(9): 153-156.

Jiang Guo-jin, Cao Liang. Time-frequency Characteristics of Underwater Explosion Signal Based on Hilbert-huang Transform[J]. Ship Electronic Engineering, 2020, 40(9): 153-156.

[97] 吴成, 廖莎莎, 李华新, 等. 基于Matlab方法水下爆炸声信号的特征提取及其分析[J]. 北京理工大学学报, 2008, 28(10): 851-855.

Wu Cheng, Liao Sha-sha, Li Hua-xin, et al. Extraction and Analysis of the Features of Underwater Explosion Signal Based on the Matlab Method[J]. Transactions of Beijing Institute of Technology, 2008, 28(10): 851-855.

[98] 贾虎, 郑伟花, 罗强. 基于HHT的金属导爆索水下爆炸信号时频特性研究[J]. 工程爆破, 2015, 21(3): 5-8, 17.

Jia Hu, Zheng Wei-hua, Luo Qiang. The Characteristics of Time Frequency Signal Based on Hilbert-huang Transform in Underwater Explosion By Metal Detonating Cord[J]. Engineering Blasting, 2015, 21(3): 5-8, 17.

[99] 贾虎, 沈兆武. 纤维爆炸索水下爆炸声信号特征的小波分析[J]. 振动与冲击, 2011, 30(9): 243-247.

Jia Hu, Shen Zhao-wu. Acoustic Characteristics of Underwater Continuous Pulse Shock Wave[J]. Journal of Vibration and Shock, 2011, 30(9): 243-247.

[100] 范志强, 马宏昊, 沈兆武, 等. 水下连续脉冲冲击波的声学特性[J]. 爆炸与冲击, 2013, 33(5): 501-506.

Fan Zhi-qiang, Ma Hong-hao, Shen Zhao-wu, et al. Acoustic Characteristics of Underwater Continuous Pulse Shock Wave[J]. Explosion and Shock Waves, 2013, 33(5): 501-506.

[101] Sheng Z X, Liu R Z, Guo R. Reverberation Generated by Sequential Underwater Explosions[J]. Acoustical Physics, 2012, 58(2): 236-242.

[102] 裴善报, 刘荣忠, 郭锐. 水下连续爆炸声学特性分析[J]. 南京理工大学学报: 自然科学版, 2015, 39(2): 144-148.

Pei Shan-bao, Liu Rong-zong, Guo Rui. Analysis of Acoustic Characteristics of Sequential Underwater Explosion[J]. Journal of Nanjing University of Science and Technology, 2015, 39(2): 144-148.

[103] 裴善报, 刘荣忠, 郭锐. 基于小波变换的水下连续爆炸声信号特征分析[J]. 爆炸与冲击, 2015, 35(4): 520-526.

Pei Shan-bao, Liu Rong-zong, Guo Rui. Analysis of Characteristics of Sequential Underwater Explosion Sound Signal Based on Wavelet Transform[J]. Explosion and Shock Waves, 2015, 35(4): 520-526.

[104] Guo R, Zhou H, Sheng Z, et al. Long-Range Reverberation of Sound Signals Generated by Sequential Underwater Explosions[J]. Journal of Computational & Theoretical Nanoscience, 2016, 13(4): 2401-2406.

[105] 易流. 基于小波变换的深水条件下爆炸冲击波信号研究[D]. 武汉: 武汉科技大学, 2015.

[106] 孙钟阜, 盛振新, 刘荣忠, 等. 基于Hilbert-Huang变换的水下爆炸声信号分析[J]. 鱼雷技术, 2013, 21(3): 189- 192.

Sun Zhong-fu, Sheng Zhen-xin, Liu Rong-zhong, et al. Analysis of Underwater Explosion Signals via Hilbert- Huang Transform[J]. Torpedo Technology, 2013, 21(3): 189-192.

[107] 刘琳, 魏明涛, 孙振新. 基于爆炸声源的多基地远程探测技术研究[J]. 指挥控制与仿真, 2019, 41(1): 99-103.

Liu Lin, Wei Ming-tao, Sun Zhen-xin. The Study of Multi-base Remote Detection Technology Based on the Explosion Source[J]. Command Control & Simulation, 2019, 41(1): 99-103.

[108] 黄聪, 朱伟锋, 李迪. 基于爆炸声源的远程水下目标定位方法[J]. 中国舰船研究, 2020, 15(6): 176-181.

Huang Cong, Zhu Wei-feng, Li Di. Remote Localization Method for Underwater Target Based on Explosive Sound Sources[J]. Chinese Journal of Ship Research, 2020, 15(6): 176-181.

[109] 张朝金, 莫亚枭, 孙炳文, 等. 半经验关系与匹配场联合处理的爆炸声源快速定位[J]. 声学学报, 2021, 46(5): 641-652.

Zhang Chao-jin, Mo Ya-xiao, Sun Bing-wen, et al. Underwater Explosive Source Localization Based on Semi- empirical Relationships and Matched Field Processing[J]. Acta Acustica, 2021, 46(5): 641-652.

[110] 李继民. 水下连续爆炸声信号对声自导鱼雷的对抗分析与研究[D]. 南京: 南京理工大学, 2006.

[111] 曾星星. 水声干扰弹对声自导鱼雷干扰机理与仿真研究[D]. 南京: 南京理工大学, 2012.

[112] Kedrinskii V K. Hydrodynamics of Explosions: Experiments and Models[M]. Berlin: Springer, 2005.

[113] 尚德江, 张仁和. 新型宽带爆炸声源及海底参数反演[J]. 声学技术, 2003, 22(z2): 158-160.

Shang De-jiang, Zhang Ren-he. Geoacoustic Inversion by Using the New Kind of Broadband Bomb Signals[J]. Technical Acoustics, 2003, 22(z2): 158-160.

[114] 周鸿涛, 魏士俨, 杨燕明, 等. 用定深爆炸声源反演海底声学参数[J]. 应用海洋学学报, 2015, 34(4): 586-594.

Zhou Hong-tao, Wei Shi-yan, Yang Yan-ming, et al. Inversion of Sea Bottom Geoacoustic Parameters Using Underwater Explosion at Fixed Depth[J]. Journal of Applied Oceanography, 2015, 34(4): 586-594.

[115] 徐东, 李风华, 郭永刚. 利用脉冲声反演深海海底声学参数[C]//2016年全国声学学术会议论文集. 武汉: 中国声学学会, 2016: 192-195.

Progress and Prospect of the Acoustic Effects of Underwater Explosions

GUORui, YU Yang-hui

(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)

Sound sources generated by underwater explosions exhibit the characteristics of high power, wide frequency band, and nondirectivity and are applicable to marine resource detection, hydrological environment inversion, underwater small stealthy target detection, and underwater acoustic countermeasures. Herein, information on the acoustic radiation mechanisms of two features of sound sources, namely, shock waves and ideal bubble pulses, are summarized. Underwater acoustic propagation and reverberation models used to describe the propagation and reverberation effect of the underwater explosion sound sources in the acoustic field model are analyzed; additionally, an overview of typical signal analysis methods and the acoustic characteristics of the sound sources is presented. In addition to the characteristics of the sound sources, typical engineering applications of underwater explosions are introduced. Finally, some future developments of investigations pertaining to the acoustic effects of underwater explosions based on high-explosive materials, the reverberation prediction of explosions, and the engineering applications of sound sources generated by arrays of multipulse explosions are presented. This review can serve as a reference for future studies related to the acoustic effects of underwater explosions.

underwater explosion; sound generating mechanisms; acoustic field model; acoustic characteristic

郭锐, 俞旸晖. 水下爆炸声学效应研究现状与展望[J]. 水下无人系统学报, 2022, 30(3): 266-282.

TJ6; U674.7; O427.9

R

2096-3920(2022)03-0266-17

10.11993/j.issn.2096-3920.2022.03.001

2022-05-10;

2022-06-06.

国家自然科学基金项目资助(11972197).

郭 锐(1980-), 男, 博士, 教授, 主要研究方向为水下爆炸声学效应.

(责任编辑: 杨力军)