大密度比双气泡在孔板结构微通道内上升行为的格子Boltzmann 方法模拟

严 裕，娄 钦，*

(1. 上海理工大学 能源与动力工程学院，上海 200093；2. 上海市动力工程多相流动与传热重点实验室，上海 200093)

0 引 言

气泡在复杂微通道内的流动现象广泛存在于自然界和工业生产过程，如沸腾现象、页岩气开采、燃料电池的使用等。例如在燃料电池中气泡间的碰撞和合并时常发生，气泡在液体中的运动和相互作用直接影响相间的接触时间和接触面积，并改变气液间的传热传质[1]，进而影响其使用性能[2-4]。因此对气泡进行微通道内的流动研究以及工业生产过程中的优化具有十分重要的意义。

学者们对复杂微通道内的气泡流动问题进行了大量的实验研究。Chen 等[5]研究了高黏度流体中气泡在孔板通道内上升时的形状变化，发现气泡穿过孔板通道后变为“月牙状”。Corapcioglu 等[6]提出采用定量方法预测气泡在粗糙多孔介质中的上升速度，其预测结果表明气泡的上升速度经过很短的时间后会达到平衡。Dawson 等[7]研究了在恒定体积流量中孔板微通道内气泡的流动过程，发现随着流速的增加，气泡的后尖端速度发散且气泡尾部变薄向中间收缩回主体。

以上实验结果得到了气泡运动过程中的直观现象和宏观规律，为人们认识气泡在通道内的运动规律提供了理论基础。然而由于实验方法难以捕获微孔内的流动细节，采用数值模拟来研究两相流动问题也逐渐成为人们研究气泡运动的一种常用方法[8-9]。Sussman 等[10]应用Level-set 方法，研究了单个气泡上升过程中的界面形变以及破裂现象，发现随着表面张力和黏度比的增加，气泡越不容易发生变形和破裂现象；而随着雷诺数的增加气泡的变形会越来越剧烈。Sun 等[11]利用格子Boltzmann 方法模拟了单个气泡在含三个半圆形障碍物的通道内上升的问题，发现了障碍物的存在可以影响气泡的运动形态，使其运动轨迹发生偏转。Lou 等[12]通过两相流格子Boltzmann模型，模拟研究了气泡在浮力作用下上升并通过复杂微通道的问题。研究发现障碍物表面润湿性越强，气泡变形越剧烈、气泡终端速度越小；且随着障碍物半径的增大，气泡的终端速度呈线性减小。

以上研究揭示了一些气泡在复杂微通道内的运动机理，但主要集中于单气泡的研究，较少涉及多气泡在复杂微通道内的运动行为，且大部分研究只能考虑较小的气液密度比。因此，本文选用Liang 等[13]基于Allen-Cahn 相场理论提出的大密度比格子Boltzmann 模型，对两个上下排列的气泡在含孔板结构的微通道内的运动形态进行研究；主要调查了Eo数、气泡之间的相对大小、两气泡之间的距离以及气泡和孔板之间的距离等因素对两个气泡变形、合并、分裂的动力学行为以及气泡穿过孔板的质量和通过时间的影响。

1 数值方法

2 物理问题

图1 D2Q9 速度模型示意图Fig. 1 Discrete velocities for D2Q9 model

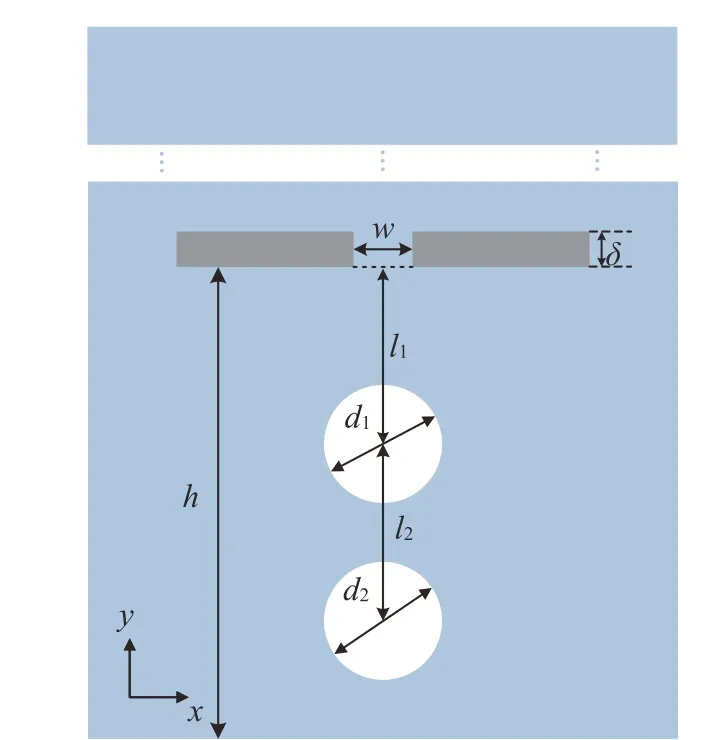
图2 模型示意图Fig. 2 Model sketch

3 模型验证

3.1 拉普拉斯验证

在本文验证中，初始气泡半径选20、25、30、35、40 这五种情况，并考虑不同表面张力σ= 0.2、0.4、0.6、0.8、1.0，模拟结果如图3 显示。气泡半径的倒数与表面张力成正比，模拟结果与Laplace 定律吻合，证明了本文所使用模型的准确性。

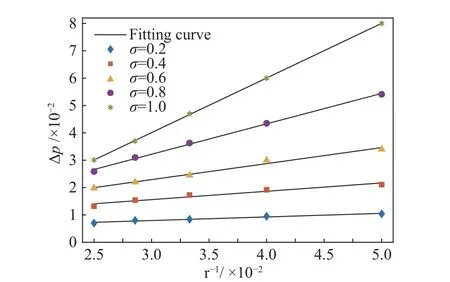
图3 Laplace 验证Fig. 3 Numerical validation

3.2 气泡在光滑通道内上升行为

气泡在光滑壁面通道内受浮力上升的问题与本文所要研究的问题相似, 且已有学者对该问题进行了大量研究, 因此本小节将采用该算例验证模型的正确性。模拟计算区域为Lx×Ly=80×300，液相密度ρl=1 000.0， 气泡密度 ρg=1.0， 气泡半径r=20，界面厚度W=3.0 ，初始时刻气泡圆心设在（Lx/2，40）处。边界条件设置：左右为无滑移固壁，上下为周期边界。

考虑Eo=5、10、20、40 四种工况，Re数固定为17.7。表1 列出了不同工况下，本文所使用的LBM方法和其他数值方法得到的气泡稳定形状对比，可以看出随着Eo数的增大，气泡从球形变为上凹的球帽形。本文得到的结果与Takada 等[16]使用双流体LBM 模型得到的模拟结果以及Ren 等[17]使用相场LBM 法模拟小密度比气泡得到的模拟结果高度相似，且在大密度比工况下得到了数值稳定的结果。之后统计气泡终端速度，如表2 所示，并与Alizadeh 等[18]和VOF 方法[19]进行对比。本文结果与两者结果一致，故本模型适用于研究气泡动态行为。

表1 不同 Eo数下气泡稳定形态Table 1 Bubble shapes at steady states under different E o numbers

表2 不同 E o 数下气泡终端速度Table 2 Terminal velocities of bubble under different E o numbers.

4 数值结果与分析

本文中主要研究Eötvös数（Eo）、气泡之间的相对大小和气泡的初始相对位置对气泡在孔板微通道内流动过程的影响。

4.1 E o数的影响

的中间以外，上方气泡与下方气泡在两侧也开始合并，导致上下方气泡之间包裹两个极小液泡（t∗=7.10）；随后在表面张力作用下液泡从两侧被排出，此时通道内的两个气泡在孔板附近完全合并形成一个完整的大气泡（t∗=9.98），大气泡通过孔板通道后在孔板正下方残留两个小气泡，而其余部分通过孔板后在孔板上方近似恢复为椭球形（t∗=18.13）。

图4（b）所示为Eo=10的工况，此时气泡表面张力相对于浮力减小，因此两个气泡在上升的过程中都有较大的形变。上方气泡下表面向上凹陷，在两端形成尾翼，下方气泡水平拉长且上表面向上凸起与上方气泡下表面近似贴合；t∗=7.09时刻下方气泡的顶点与上方气泡中间接触，接着上方气泡两端向下弯曲，下方气泡上表面两侧与其接触，气泡间形成两个液泡，因为表面张力相对浮力减小，所以此时形成的液泡比Eo=5的工况下生成的大。由于孔口的阻力小于两侧，下方气泡质量主要从中间的接触点并入上气泡，t∗=9.19时刻上气泡与两端断裂，其两端并入下气泡两端，液泡也被气泡从断口排出。随后在t∗=11.04时刻两个气泡合成了一个主气泡（能够排出的气泡），在部分质量穿过孔口后，主气泡运动速度增大与孔板正下方部分质量再次断裂，这些质量最终残留在孔板下方。主气泡在穿过孔口后由于拉伸再次破裂出一个小气泡，该小气泡尾随主气泡上升（t∗=20.76）。对比图4（a）和图4（b）可以发现，随着Eo数增加，气泡在穿越孔板前后的形变更明显。

图4（c）为Eo=20得到的气泡运动过程。从图中也发现随着Eo数的持续增大导致气泡变形和断裂更严重。例如在气泡的上升过程中，上方气泡尾端形成了更长的尾翼，下方气泡也更扁长。而更多的接触面积和更小的表面张力也让上下两个气泡间形成更多的接触点（t∗=7.36），两个气泡中间存在着更多更大的液泡，尽管此时气泡在过孔板通道前依旧可以将液泡挤出，但也导致主气泡和其两端的连接容易断裂（t∗=11.30），残余在孔板下的气泡质量增加。主气泡在通过孔板后也分裂出一个更大的尾气泡（t∗=20.76）。而当Eo数增加到40 时（图4（d）），上下气泡发生了多次接触、合并与破裂的过程。在主气泡通过孔板通道后，气泡内部还夹带着一个小液泡与其上升了一段距离才被排出（t∗=21.55）。从图中可以看出四种工况下气泡首次接触的时间分别为t∗=6.71、7.09、7.36、7.61，接触时上气泡都已进入孔道，主气泡到达计算区域上方的时间如图5 所示。因此随着Eo数的增大，气泡接触时间越晚，气泡间接触面积增大，接触点随之增多；接触点的增多并不能促进两气泡的合并，反而导致中间生成更多液泡，加剧气泡分裂，气泡通过孔板通道需要的时间也越长。气泡到达顶部的所需时间随着Eo数 的增大而增多，并且当Eo数大于10 后呈线性上升的趋势。

图4 不同 Eo数下气泡运动过程Fig. 4 The temporal evolution of bubbles under different E o numbers

上述四种工况下，Eo数对两个气泡通过孔板通道的剩余质量比Ms有影响，为了分析这种影响，本文对不同Eo数下的气泡剩余质量进行统计。由图5 对Ms曲线的拟合发现，气泡剩余质量的变化趋势随Eo数的增加呈负指数级地减小；减小是因为随着Eo数的增大，气泡表面张力相对于浮力减小，气泡难以维持初始形状，其在上升和变形的过程中更容易包裹液泡，并更容易发生破裂，导致残留在孔板下方。而随着Eo数的持续增大，气泡的最终剩余质量趋于稳定；这是因为尽管气泡被拉伸，但气泡初始位置与孔板间的距离导致气泡还未充分形变便到达了孔板位置，有一半多的质量处在孔口正下方且最终通过孔板。

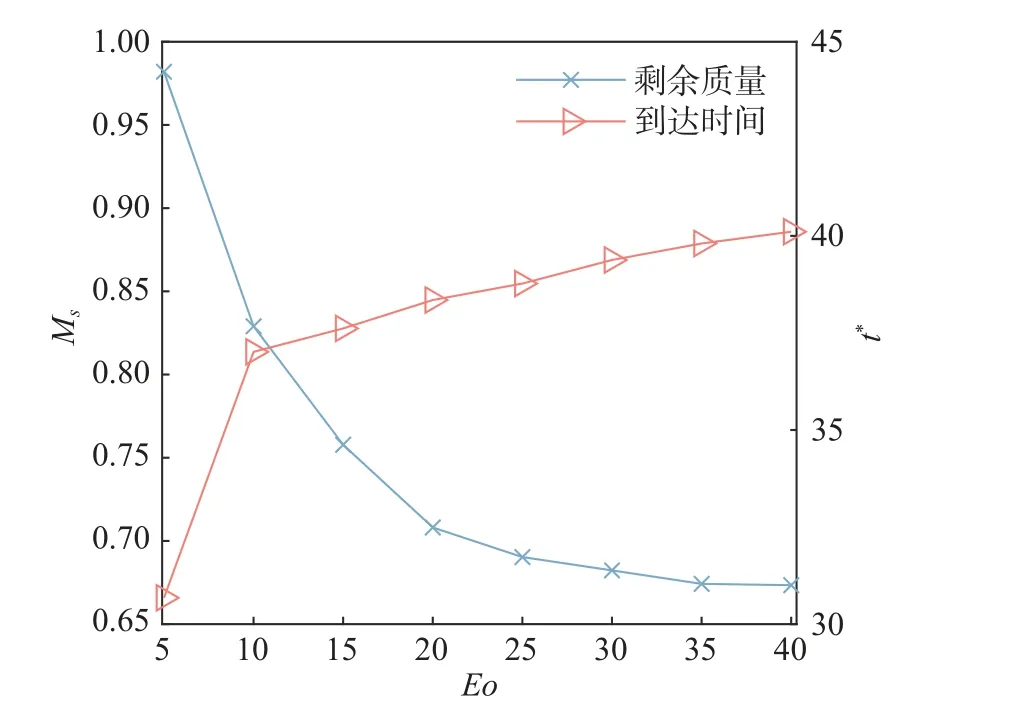
图5 不同 Eo数下剩余质量比和气泡到达顶部时间Fig. 5 The variation of residual mass and the time for bubble to reach the top for different E o number

4.2 气泡相对大小的影响

本小节研究了气泡相对大小对气泡通过孔板微通道的影响。数值模拟中参数设置为 σ =0.624；为了方便比较，选择孔口间距w作为参照尺寸，上下两气气 泡 大 小d1:d2分 别 设 为 2.4w:1.5w、 2.0w:2.0w、1.5w:2.4w；三种气泡方案的质量和近似；两气泡初始位置分别设为（x1c，y1c） =（Lx/2 ， 100）和（x2c，y2c）=（Lx/2，40）。

图6（a）展示了d1:d2=2.4w:1.5w，即上方气泡大于下方气泡时气泡穿过孔板的运动过程。如图所示，在t∗=9.99时下方气泡接触到上方气泡，此时上方气泡部分已经穿过孔板通道，下方气泡与上方气泡尾翼接触并将一个直径约为1 .0w宽的液泡包裹在内。液泡随气泡的上升与其一起穿过孔道。当液泡处于孔板通道内时气泡被夹断分成上下两个气泡（t∗=11.56），之后上气泡虽然已经穿过孔板通道，但由于形变较严重，维持了较低的运动速度。当液泡受到下气泡对其的推动力后从孔口被排出，下气泡加速向上运动与上气泡合并（t∗=17.35），之后尾部再次破裂产生一个小气泡，并在表面张力的作用下，逐渐恢复为球帽状。

图6（b）给出了上下两气泡直径相等时（d1:d2=2.0w:2.0w）气泡的上升过程。如图所示，上气泡靠近孔板后拉伸为长条状，而下气泡也被拉长，上气泡下方和下气泡上方贴合，在中间和两端产生接触点（t∗=7.36），气泡内部形成两个液泡。上气泡与其两端断开，接着液泡从断口排出（t∗=11.04），上气泡端部汇入下气泡的端部。但此时下方气泡质量主要在中部并且已并入上方气泡，其与两端的连接也迅速断开。主气泡加速通过孔板通道并继续上升（t∗=15.51），之后在上升过程中气泡尾部又断裂出一个小气泡。

上方气泡直径小于下方气泡（d1:d2=1.5w:2.4w）的结果如图6（c）所示。在t∗=6.05时上方气泡靠近孔板后变扁平状中间凸起。下方气泡从中间和两侧同时接触到上方气泡，形成两个小液泡。与气泡直径相等的情况不同的是，下气泡主要从两端汇入上气泡，再从两端向孔板通道中间收缩（t∗=11.04），过程中两个小液泡被挤压合并为一个直径为w的液泡。液泡在孔板通道下方主要受到气泡对其的表面力，方向从向上转为向中间，液泡几乎处于静止状态，未跟随气泡上升，随后液泡被主气泡从下表面排出。主气泡穿过孔板通道继续上升。

图6 不同气泡直径下气泡运动过程Fig. 6 The temporal evolution of bubbles with different diameters

为了研究气泡相对大小对气泡通过孔板通道后剩余气泡质量的影响，增加了几组气泡直径比不同的工况以便比较。图7 给出了三组相同变化比例但不同初始质量和的情况，统计了气泡穿过孔板后的剩余质量以及气泡运动到计算区域上方的时刻。从图7中间组可以看出，当上气泡质量大于下气泡质量时，上气泡位于孔板正下方部分质量接触到下气泡后在表面张力作用下向中间收缩，最终有较多的剩余质量可以达到顶部。而当下方气泡大于上方气泡时，两气泡发生合并的时间和位置提前，尽管下方气泡是从两侧汇入上气泡，但两个气泡形变程度较小，合并的气泡质量向孔口方向移动，故最终穿过孔板通道的质量比前者情况少。从中间组可以看出上下气泡直径对比度越大，剩余质量越多；而当上下两个气泡大小相等，穿过孔板到达通道上半部分的剩余质量最少，为0.82。在相反的直径比例下，质量大的气泡处在上方的情况最终的剩余质量始终比处在下方的情况多。另外，随着下方气泡相对上方气泡直径增大，气泡通过孔板到达顶部所需时间变短。结合图7 上下两组可以看出气泡尺寸相对孔径越小，其通过得越完整，即剩余质量越多；而较小的质量也导致其受到的浮力相对较小，到达顶部时间变慢，在不同直径比下的剩余质量和到达时间也与中间组的变化趋势相似。

图7 不同气泡直径下的剩余质量比和达到时间Fig. 7 Residual mass and the time for bubbles to reach the top for different diameters

4.3 两气泡之间的距离与气泡与孔板的距离的影响

本小节研究两气泡之间的距离以及气泡与孔板的距离对双气泡运动行为的影响。首先研究不同气泡之间距离的情况，为了方便比较，此算例也以孔板间距w作为参照尺寸，l1和l2都 表示为w的倍数。在数值模拟中设置了三组工况，首先使上气泡的位置固定不变，此时上方气泡圆心与孔板间下表面距离l1=3.0w为固定值，接着改变下气泡的位置，使上下气泡圆心之间的距离l2分 别为2.5w、 3.0w和 3.5w三种情况。此外，Eo=10，d1=d2=20。

当两个气泡圆心距离l2=2.5w时，所得到的结果如图8（a）所示。上气泡下表面和下气泡上表面的最近点距离为 0.5w，t∗=3.68时下气泡向上浮动从中间接触并入上气泡，并在上气泡到达孔板之前完成合并（t∗=6.04），气泡间未有液泡形成。合并完成后的主气泡横向拉抻，气泡中间部分质量在浮力作用下穿过孔口；在表面张力作用下气泡两侧向中间收缩穿越孔口，最快地穿过了孔板通道（t∗=12.35），穿过后恢复为球帽形并保持匀速上升运动。

当两个气泡圆心距离l2=3.0w时，上气泡下表面和下气泡上表面的最近距离为1 .0w，此时下气泡并入上方气泡的同时上方气泡准备穿过孔板通道；当t∗=8.41时下气泡先后从中间和两端接触到了上方气泡，中间夹着液泡。液泡把上气泡与其两端挤断，接着液泡从断口排出（t∗=10.77），上方气泡两端与下方气泡的两侧合并；但此时下方气泡多数质量集中在中间并已并入上方气泡。下方气泡与两侧的连接断开，继续上升。

图8（c）给出了两个气泡圆心距离l2=3.5w时的结果。从图中可以看出，t∗=9.20时刻在两个气泡合并前，上气泡中间部分已经与两侧脱离后先行穿过孔板通道，穿过孔板通道时速度上升，但其所占整体质量的比重小，平均上升速度提升不明显；两侧残余的质量与下气泡合并，t∗=12.88时上气泡离开孔板通道的同时下方气泡进入孔板通道，气泡之间存在液泡，上下两气泡运动速度均下降；当下方气泡头部穿过孔板通道并把液泡从孔板通道挤出后，其速度上升并加速和上气泡合并成一个气泡。

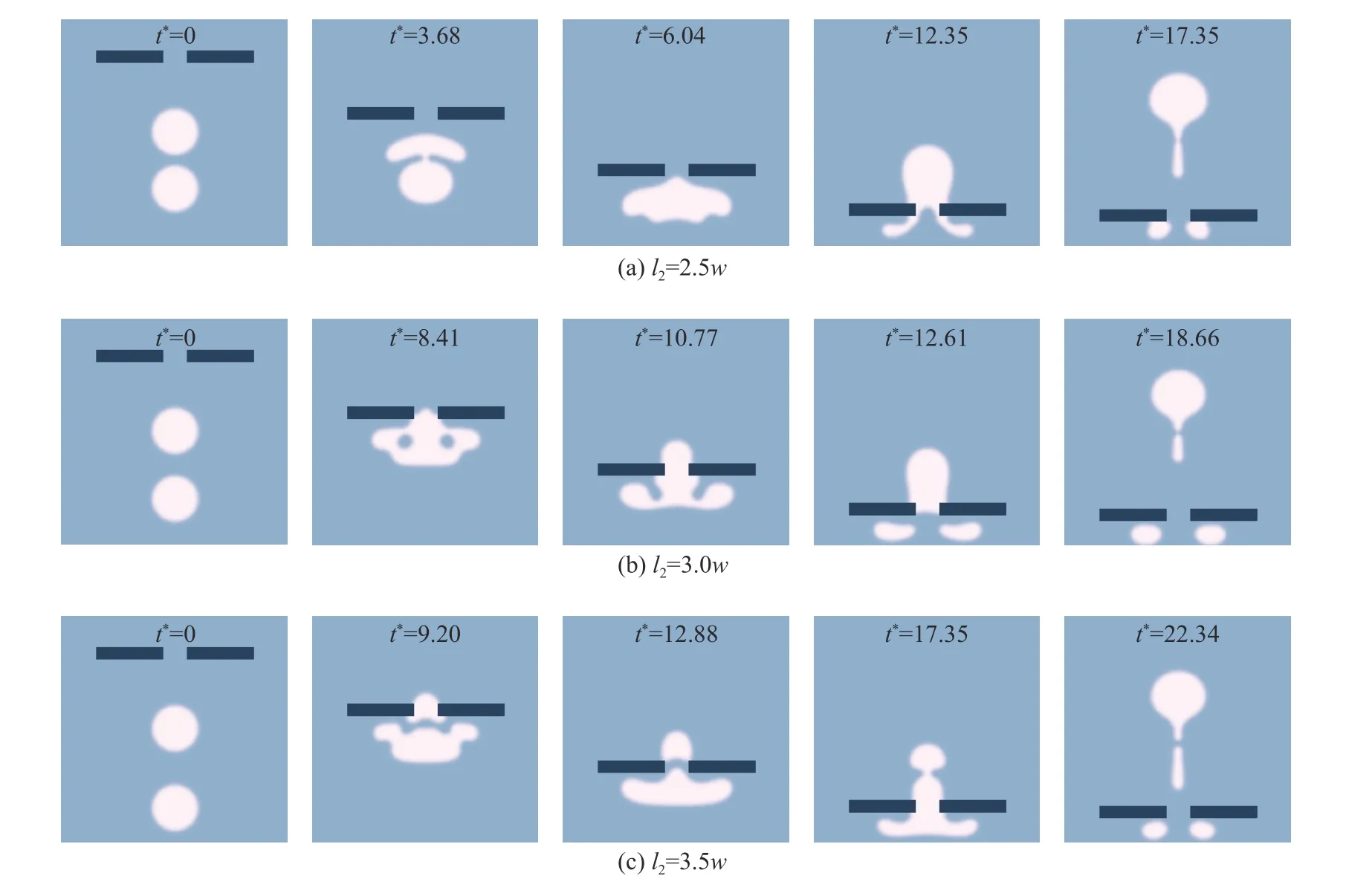
图8 气泡不同初始位置情况下气泡运动过程Fig. 8 The temporal evolution of bubbles under different initial positions

经模拟计算发现，当l1=3.0w、l2=3.3w时，几乎在上方气泡与两侧脱离的同时下方气泡与其两侧接触，而上气泡主体已开始加速上升。相比l2=3.25w的情况，两气泡主体接触的位置从孔口下方约 0.5w处跃迁到了距离孔口上方1 .5w的位置；气泡主体第一次接触的 时 间 也 从t∗≈6.0推 迟 到 了t∗≈14.2。 在l1从 2.5w增加至 3.5w的 过程中，临界的l2从 3 .1w变 化为 3 .45w。

图9 展示了两个气泡从不同位置开始上升时统计得到的速度变化曲线。从图9 可以看出，在气泡未到达障碍物通道前，气泡的上升速度变化趋势基本相同；但当上气泡与孔板的距离l1不 变时，在l2=2.5w气泡间距较小的情况下，初始运动的速度提升最大。这是因为两气泡在通过孔板通道前完成了合并，合并后的气泡受到的浮力增大；在完成合并后通过孔板通道时速度变化剧烈，作为整体通过孔道时减速更明显，通过孔道后的加速也越剧烈；之后因表面张力作用与孔板下方质量发生断裂时, 速度略微下降, 最后再度趋于平稳。而当两气泡间距增大（如l2=3.0w），两气泡在孔板下方发生接触但未完全合并，这也使其速度变化与间距较小时相同，但变化幅度更平和。如果两气泡间距进一步增大，则上气泡部分质量先进入孔道，另外部分质量并入下气泡，穿越孔道的过程分成两次，加速过程随之变为两次；其中第二次在t∗=17.35时，出现转折是在下气泡通过孔道后接触到上气泡并汇入的时刻。

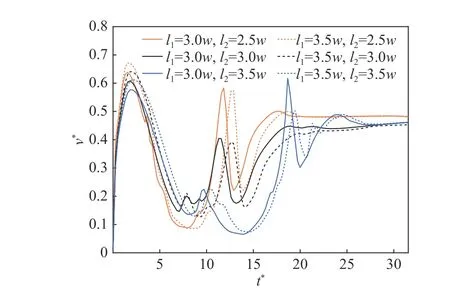
图9 不同初始位置下气泡上升的平均速度 v∗与 时间 t∗的关系Fig. 9 Average bubble velocity versus time for different initial positions

接下来研究上方气泡与孔板间的距离对双气泡运动行为的影响，这里固定两气泡间距，通过改变上气泡的位置来改变气泡与孔板的间距l1。图9 的实线和虚线分别表示l1为 3.0w和 3.5w的情况。从图中虚线和实线的对比可以发现，气泡离孔板越远（l1越大），气泡的运动相对越迟滞；初始时表现为速度上升得更高，之后在穿越孔道前后时的速度变化规律相同；气泡穿过孔板通道后又恢复到匀速运动。

为了分析气泡初始位置和初始间距对气泡通过孔板通道后剩余气泡质量的影响，本文在上述三种工况的基础上，通过改变l1的大小增加了几组工况。在不同l1和l2的情况下，气泡穿过孔板后到达计算区域上方的剩余质量进行了统计和比较，如图10 所示。在上气泡位置不变的情况下，下气泡所处位置越高（气泡之间间距l2越短），两气泡在越早的时刻合并，可以穿过孔板到达顶部的质量也越多。在气泡间距相同的情况下，上气泡与孔板的距离l1越大，通过的剩余质量反而越少。对于剩余质量，气泡间的距离比气泡与孔板间的距离更重要。结合图10 可以发现终端速度和剩余质量也存在着联系：剩余质量越多，气泡受到的浮力越大，其终端速度也越大。

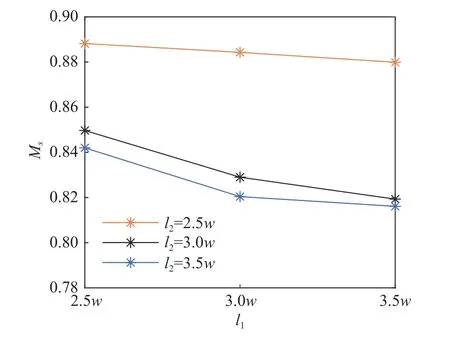
图10 气泡初始位置与剩余质量的关系Fig. 10 The relationship between the residual mass and the position of the bubble

5 结 论

本文基于大密度比两相流LBM 模型，对双气泡在含孔板微通道内的运动过程进行了研究。分别考虑了Eo数、气泡之间的相对大小和相对位置等因素对气泡在孔板通道内流动的影响，得到如下结论：

（1）随着Eo数的增大，气泡在通过孔板通道时所包裹的液泡越多，气泡容易发生变形、合并和破裂；另外当气泡在相同的初始位置上升时，随着Eo数的增大，气泡剩余质量Ms呈负指数级地减小。

（2）大气泡在上、小气泡在下时，运动过程中气泡受到的阻力更大，表现为上方气泡通过孔板的过程中形变更明显，两个气泡在孔口附近合并得更充分，通道内的残留质量较少；但到达通道顶部需要的时间更长。大气泡在下、小气泡在上时，气泡到达孔板附近的时间更快，此种情况两气泡的形变最小，气泡到达顶部所需要的时间最短。而当上下两气泡相等时，穿过孔板到达通道上半部分的剩余质量相对于其他两种情况最少。

（3）当两个气泡初始距离相近时，两气泡之间的合并通常发生在上方气泡到达孔板通道之前，此时通过的剩余质量最多；随着两个气泡之间的距离拉大，两气泡之间的合并更容易发生在上方气泡经过孔板通道时，通过的剩余质量次之；当两气泡之间的距离增加到一定程度，上方气泡穿过孔板通道并发生断裂之后，下方气泡才追上并与之合并，到达计算区域上方的剩余质量最小。另外，上下气泡初始位置同时升高也可以提高通过孔道的剩余质量。