混合梁跨度合理布置对结构内力的影响研究

曾弘毅，王成铜

(浙江工业大学 土木工程学院 杭州市 310014)

1 概述

混合梁桥由于其能充分发挥混凝土和钢材的材料性能，显著提升跨越能力及经济性，近年来得以快速发展。但主跨跨径往往受制于施工条件、经济性及其与周边环境的协调因素，通常遵从一般性原则进行设计，导致其与结构内力变化的关联性常被忽视。国内外学者对此从混合梁整体力学性能开展了一些工作。如，蒲泊舟[1]研究了重庆永川长江大桥在施工期间结构体系变换造成的整桥内力变化；谢鸿[2]建立有限元模型为探究云南省六库怒江混合梁斜拉桥的动力特性；张鹏等[3-4]通过定性与定量两个维度评估陕西渭河特大桥，并进行概念设计。贺鹏、张谢东[5-6]等分别以非对称以及对称混合梁斜拉桥的成桥阶段为工况采用有限元模拟。总的来说，当前针对混合梁桥的整体力学性能的研究多数基于混合梁桥的自身受力特点，而较少关注跨度(主跨跨径、边主跨比、结合段跨度)合理布置对内力分配的影响。

基于结构力学的连续梁桥半结构的推演，获得了桥墩弯矩、钢混结合段弯矩以及中跨弯矩的理论解，并将其应用于探索中边跨比以结合段与中跨比两个因素及对关键节点内力的影响。

2 基于结构力学的内力推演

本研究力求完整反映桥梁结构的受力特点以及不影响结果准确性的前提下，将桥梁结构简化为力学模型。依据对称性将研究对象三跨连续混合梁简化为图1所示的连续梁桥半结构，边跨长度L1，中跨混凝土段长度L2，中跨钢混结合段长度L3；混凝土箱梁及钢箱梁的自重荷载集度分别为q1、q2；混凝土箱梁及钢箱梁的抗弯刚度分别为EcIc、EsIs。

图1 连续梁桥半结构示意图

为更全面地评估跨度分配对结构内力的影响，选取了桥梁桥墩、钢混结合处及中跨三个控制点的弯矩值作为研究对象，分析边主跨比K1及中跨钢箱梁与混凝土长度比K2两个指标对控制点内力的影响。依据该研究目的，连续梁桥的基本结构如图2所示。

图2 基本结构示意图

依据位移法，可列出该结构的基本方程：

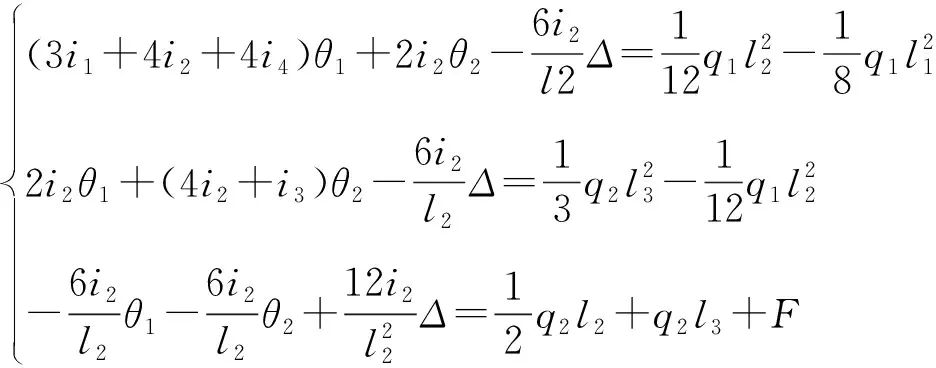
(1)

式中:θ1为桥墩处控制点处单位转角;θ2为钢混结合处控制点单位转角;Δ为钢混结合处控制点单位竖向位移。

根据克拉默法可获得该方程组的解：

整理可得:

将θ1、θ2、Δ代入基本方程组后可得各控制点处的弯矩值。

3 算例

依托湖州长兴画溪大桥，45m+80m+45m钢混混合梁的立面图示于图3。边跨及中跨混凝土箱梁采用混凝土C50，桥墩采用混凝土C25，中跨段钢箱梁采用Q345C钢材，预应力钢绞线强度为1860MPa。

图3 画溪大桥立面图(单位：cm)

中跨40m长桥钢箱梁断面与主跨混凝土箱梁断面宽度相同，一致采用四箱断面，箱顶宽为18.75m，悬臂长度为2.5m，梁底宽为13.79m，如图4所示。横隔板沿桥长每1.5m设置一道，其中交替设置大小横隔板，采用螺栓连接箱横隔板；钢箱梁内部顶、底板处设置纵向加劲肋以增加钢箱梁的结构刚度，如图5所示。

图4 画溪大桥断面图(单位：cm)

图5 画溪大桥1/2钢箱梁平面图

提取该桥的截面特性及荷载集度并代入上文推演的控制点弯矩理论解中，可以获得该依托工程各控制点位的弯矩，基于此，建立中跨钢箱梁的最大弯矩受中边跨比K1及中跨钢箱梁与混凝土箱梁长度比两因素对控制点弯矩的影响，通过控制某一因素为恒定值，研究另一因素对控制点弯矩的变化。

4 结果分析

依据图6展示的结果可以发现当K1为恒定数值时，K2的增加带来桥墩处负弯矩显著降低的影响，其降幅于K1=0.3、0.4、0.6、0.7上时分别为37.5%、36.8%、38.5%及36.4%。此外，可以见得K2的增加对中跨钢箱梁弯矩增大很小。值得注意的是，随着K2的增大，钢混结合段处所受负弯矩不断增加，经历了从正弯矩变为负弯矩，且在K2位于0.4～0.5内某一点弯矩达到0。

图6 基于不同中边跨比K1，钢箱梁与混凝土长度比K2对控制点弯矩的影响

K1对控制点弯矩的影响示于图7，钢混结合段处弯矩受K1的影响较小，但其负弯矩随着K2的增大而增大，当K2=0.3时其弯矩为正逐渐变化到K2=0.7时M约为-105kN·m。

图7 基于不同的中跨钢箱梁与混凝土箱梁长度比K2，中边跨比K1对控制点弯矩的影响

桥墩处负弯矩随K1的增大而显著变小，在K2=0.3、0.5、0.6、0.7上时负弯矩降幅分别为49.7%、52.6%、53.1%、53.3%。由此也可知桥墩控制点处负弯矩大小受制于K2的水平,并且随着K1的增大，其负弯矩下降速率也将变大。对于钢箱梁跨中弯矩而言，该控制点的正弯矩值随K1的增大而减小，直至K1=0.5～0.6范围内达到最小，随后又将继续增大。

由上述结果可知，K2的变化对中跨钢箱梁段的弯矩影响不明显，而对钢混结合段处和桥墩处弯矩影响较为显著，故若需寻找该案例桥的最合理的跨度分配方案则需重点关注上述两个控制点。对于钢混结合段处弯矩而言，其对K1的变化不敏感，显著受制于K2的影响，以K2=0.3～0.5分配跨度较为合适。而对于桥墩控制点弯矩而言，其与K1、K2呈显著的正相关。综合上述分析，对于该案例桥，在合理范围内设置更大的K1，并将K2控制在0.3～0.5为宜，该混合梁的内力将趋于一个更加合理的状态。

5 结语

基于位移法推演三跨混合梁桥关键截面内力，应用该解分析及讨论湖州长兴大桥各跨跨径布置及结合段长度对结构受力性能的影响，并以此给出各跨长度的合理分配的建议。主要结论为:

(1)中跨钢箱梁的最大弯矩受中边跨比K1及中跨钢箱梁与混凝土箱梁长度比K2的影响较小，而钢混结合段处与桥墩处弯矩受上述两因素影响较大。

(2)钢混结合段处弯矩受中跨钢箱梁的最大弯矩受中边跨比K1的影响极小，但受中跨钢箱梁与混凝土箱梁长度比K2的影响极大。当中跨钢箱梁与混凝土箱梁长度比K2较小时，钢混结合段控制点承受正弯矩作用，随着K2的增大，其弯矩值由正转负并不断增大。桥墩处弯矩与K1、K2呈显著的正相关。

(3)综合考虑三个控制截面的内力情况，在合理范围内增大K1，并将K2控制在0.3～0.5内，可较大程度发挥混凝土箱梁的作用，使该案例桥的受力性能更加合理。