G312合六叶公路桥风振特性研究

罗 祎，杜江波

(1.中铁大桥勘测设计院集团有限公司 武汉市 430000； 2.中铁五局集团华南工程有限责任公司 东莞市 523000)

大跨径钢箱梁桥具有自重小、整体刚度大、结构强度高等优点，因而被广泛应用于我国的桥梁建设中[1-2]。大跨径钢箱梁桥在风荷载作用下的振动，可主要分为颤振、驰振与涡振等[3-4]，其中前两种风致振动风险被要求在设计阶段排除[5]，而对于涡振，则一般通过保证结构所必需的刚度与构件疲劳性能来避免桥梁结构的风致振动破坏。以合六叶公路桥为工程背景，对其风致振动特性进行分析研究。

1 工程概述

引江济淮工程G312合六叶公路桥位于江淮沟通段 K42+271m 处，跨越江淮沟通段航道，上部结构由 4 幅跨径布置均为(100+180+100)m 的变高度直腹板连续钢箱梁组成，桥面全宽52.5m。4幅钢箱梁均采用单箱单室结构，中间支点处梁高为 9m，中跨跨中直线段和边跨端部直线段梁高为 4.5m，变高段底面线形为半径 R=824.028m 的圆曲线。钢箱梁顶板设置单向 2%的横坡，底板水平。其中，第1幅和第4幅钢箱梁关于道路中心线对称，第2幅和第3幅钢箱梁关于道路中心线对称。

第1幅和第4幅钢箱梁顶板宽度为 11.75m，其中箱宽 6.25m，两侧悬臂宽度均为 2.75m。第2幅和第3幅钢箱梁顶板宽度为13.25m，两侧悬臂宽度均为3.5m。其横桥向布置见图1。

图1 合六叶公路桥横桥向布置

合六叶公路桥具有“跨度大、柔性、钢箱梁弱阻尼”的结构特点，同时，桥址处的风动环境复杂，可能诱发较大的风致响应、主梁气动稳定性和涡激振动等问题，为确保桥梁在施工阶段的抗风安全性，及运营阶段的行车舒适性，须对合六叶公路桥的风致振动特性进行分析研究。

2 自振特性分析

根据Midas civil三维有限元分析计算模型，计算得到了该桥的自振特性，表1与表2给出了该桥前5阶模态频率与振型描述。

表1 合六叶公路桥前5阶模态频率与振型描述

表2 合六叶公路桥前5阶模态振型参与质量

3 减振前风致振动分析

根据现行规范[5]，合肥市重现期十年的设计风速W1为25.5m/s，合肥市百年一遇设计风速W2为27.9m/s。对合肥市气象站1973年至2014年间的风速、风向气象数据进行分析，合肥市全年无主导风向。因此，合肥市重现期十年的设计风速W1设为25.5m/s，重现期百年的设计风速W2设为27.9m/s。选择地表类别为规范B类，得设计基准风速Ud=29.25m/s。

合六叶公路桥横桥向为四幅布置，从河道上游至下游编号为1#桥、2#桥、3#桥及4#桥，结合规范规定，不考虑风荷载效应和静风稳定性效应，仅对脉动风作用下引起的动力响应进行分析(涡激共振、颤振、驰振和抖振)，分析结果如下所述：

(1)驰振稳定性分析

由于箱梁为箱形钢构件，驰振力系数取-1.0～-1.4，按式(1)计算钢箱梁的驰振稳定性临界风速。

(1)

式中：Ucg为驰振稳定性临界风速；m为构件单位长度质量；ωb1为结构一阶弯曲圆频率；ξs为结构或构件阻尼比，钢箱梁主梁结构阻尼比取0.003；D为构件断面的特征高度；Cg为结构断面驰振力系数。

其驰振力系数取-1.4，构件断面的特征高度为4.5m，根据上式计算主梁驰振临界风速最大值Ucg=87.3m/s，箱梁设计基准风速Ud=29.25m/s，Ucg>1.2Ud，满足规范要求。

(2)涡激共振验算

按规范对合六叶公路桥各桥进行涡激共振验算，1#桥和4#桥一阶竖弯涡激共振起振风速Uvh=17.33m/s，扭转涡激共振起振风速Uvt=23.42m/s；2#桥和3#桥一阶竖弯涡激共振起振风速Uvh=19.8m/s，扭转涡激共振起振风速Uvt=26.88m/s。由于合六叶公路桥各桥的Uvh与Uvt均小于合肥市重现期十年的设计风速W1，因此本梁桥存在涡激共振的危险，应利用全桥气动弹性模型试验进行涡激共振检验或采取风振控制措施进行抑制。

(3)颤振稳定性

按规范要求对合六叶公路桥各桥进行颤振稳定性验算，得1#桥和4#桥的颤振稳定性指数If=2.15，2#桥和3#桥的颤振稳定性指数If=2.06，并按式(2)验算颤振临界风速。

Uf=ηsηαUco

(2)

式中：ηs为形状系数，本桥梁结构取0.65；ηα为攻角的效应系数，本桥梁结构取0.7。

计算得1#桥和4#桥的颤振临界风速65.7m/s，2#桥和3#桥的颤振临界风速64.2m/s，满足规范的相关要求。

(4)抖振

按规范规定进行抖振效应的验算。根据Karman风速谱，采用MATLAB编写生成横风向脉动风时程曲线，时长30s，采样频率10Hz，时间间隔0.01s，如图2所示。将脉动风时程导入Midas进行时程分析，得到1#桥和4#桥的抖振响应，结果显示跨中位置处位移响应和加速度响应的最大响应幅值均不大，其中加速度最大响应幅值为0.44m/s2。

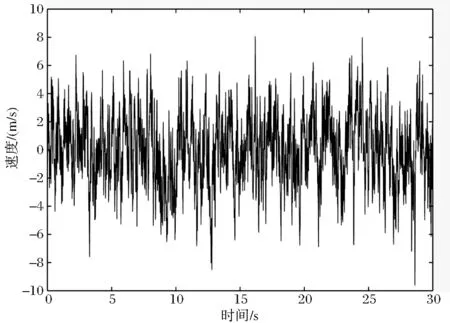
图2 合六叶公路桥桥面高处脉动风时程曲线

为进一步研究风荷载引起桥梁振动的不利情况，对合六叶公路桥在一阶与三阶共振作用下的谐响应进行分析。加载频率分别为一阶与三阶时的结构固有频率，加载幅值为对应脉动风速的较大值，本文取6m/s。结果表明：在第一阶谐响应下，1#桥和4#桥位移响应和加速度响应的最大位移和加速度幅值与上述脉动风作用下的值相近，主跨跨中位置响应幅值约为两边边跨位置的两倍左右，其整体呈现发散增长趋势；在第3阶谐响应下，1#桥和4#桥的加速度共振响应的幅值为3.18m/s2，呈发散趋势，超出了规范规定的行人舒适度范围，两边边跨跨中位置的加速度响应略高于主跨跨中位置处的响应。

G312合六叶公路桥2#桥和3#桥的计算和分析方法与1#桥和4#桥的相类似，在此不再赘述。根据以上分析结果，应对本桥第1阶和第3阶的竖向振动采取减振措施。

4 TMD减振器的应用

对于风致振动现象，可采取相应的风振控制措施，风振控制分为主动控制和被动控制，主动控制的控制力由外加能源主动施加，被动控制则是通过安装减振器来降低桥梁的风振[6-7]。风振控制是通过合理选择控制力的大小与施加方式，使结构的风振反应可以满足减振设计的要求。考虑到主动控制的复杂性和操作上的难度，本桥采用结构被动控制的方式，通过加装TMD减振器以抑制风振现象。TMD减振器是调频质量阻尼器，也称为动力吸振器，主要由质量块、弹簧系统和阻尼系统组成。TMD减振器的工作原理为：将主结构的振动能量转移到辅助系统，从而实现主结构的消能减振。合六叶公路桥TMD减振器的技术参数与安装位置如表3所示。

表3 合六叶公路桥TMD技术参数及安装位置

以1#桥为例，输出安装TMD减振器后，桥梁第一阶与第三阶的共振响应大幅减小，振动响应呈收敛形式，加速度峰值减小幅度达40%以上。

5 结语

G312合六叶公路桥是大跨径连续钢箱梁桥，解决其在运营阶段的抗风问题是确保大桥安全服役的关键。基于有限元模型与风振稳定性验算，对桥梁的风振特性进行了研究，主要得到以下结论：

(1)合六叶公路桥一阶竖向振动频率在0.7Hz左右，一阶对称竖弯振动频率在1.88Hz左右，可以看出本桥发生风致振动的概率较大。

(2)合六叶公路桥设计基准风速Ud=29.25m/s，而1#桥和4#桥一阶竖弯涡激共振起振风速Uvh=17.33m/s，扭转涡激共振起振风速Uvt=23.42m/s，2#桥和3#桥一阶竖弯涡激共振起振风速Uvh=19.8m/s，扭转涡激共振起振风速Uvt=26.88m/s，该桥梁存在涡激共振的危险。

(3)安装TMD减振器后，可有效降低合六叶公路桥的风致共振响应，其加速度峰值的下降达到40%以上。