用裂项相消法求几种数列的前n项和

吕双海

(镇江崇实女子中学，江苏镇江，212002)

2022年全国新高考数学试卷第17题第(2)问中，考查了“裂项相消法”.数列求和的题型很多，什么时候用裂项相消法，这与题目条件的结构有关.下面谈谈如何用“裂项相消法”解决数列求和的几种题型.

【题型1】

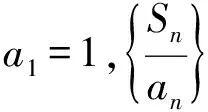
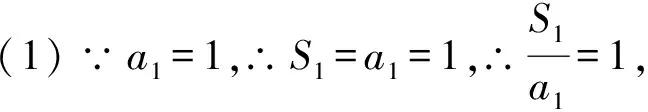
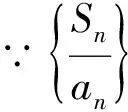
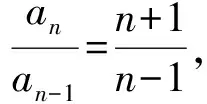
显然对于n=1也成立，

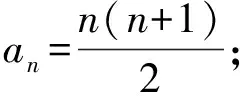
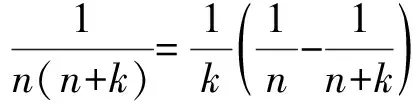
【题型2】

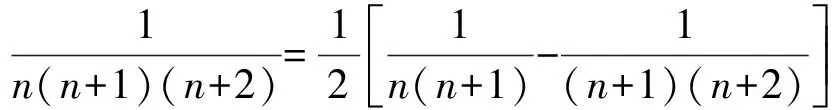
【题型3】

例3若Sn=12+22+32+…+n2，求Sn.

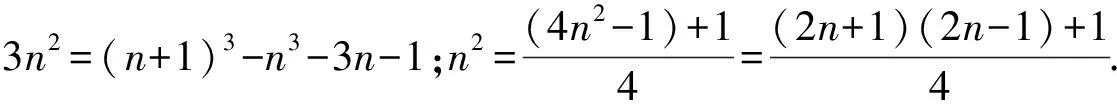
解：(方法一) ∵(n+1)3-n3=(n+1)2+(n+1)n+n2=3n2+3n+1，3n2=(n+1)3-n3-3n-1，

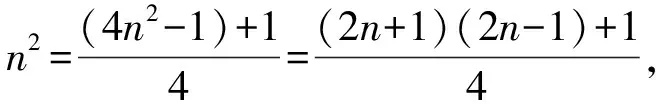
【题型4】

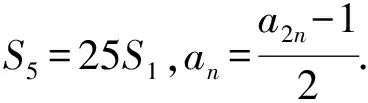
(1)求数列{an}的通项公式；

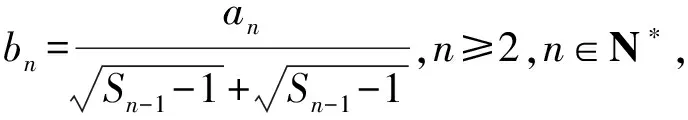
解得a1=1，d=2.

∴an=1+2(n-1)=2n-1.

根据(a+b)2≤2(a2+b2)，a，b>0，a≠b.

【题型5】

例5已知各项均为正数的等差数列{an}中，2a2，a6，a9成等比数列，且a3=3.

(1)求数列{an}的通项公式；

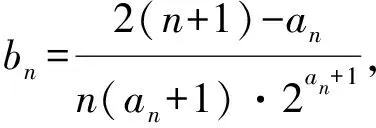
解：(1)设等差数列{an}的公差为d.

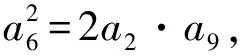
即(a1+5d)2=2(a1+d)·(a1+8d)，

整理可得a1=-9d或a1=d，

而a3=a1+2d=3，且an>0，所以a1=d，解得a1=d=1，

所以an=1+(n-1)×1=n，即数列{an}的通项公式an=n；

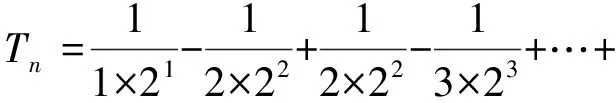
【题型6】

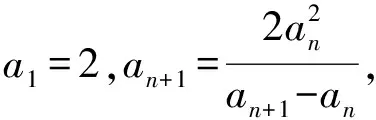
(1)求{an}的通项公式；

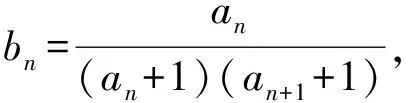
所以(an+1+an)(an+1-2an)=0，因为an>0，所以an+1+an>0，所以an+1=2an，

又a1=2，所以{an}成以2为首项，2为公比的等比数列，所以an=2n(n∈N*).

(2)由(1)知an=2n(n∈N*)，

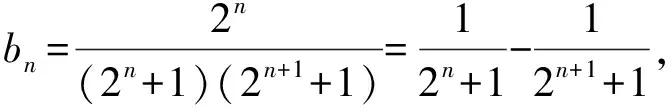
【题型7】

(1)求数列{an}的通项公式；

分析：本题通项bn中含(-1)n，所以裂项时，不能化为两项的差，而是转化为两项的和.

且a3为a1与a11的等比中项.

解得a1=2，d=3，

则an=2+3(n-1)=3n-1，n∈N*；

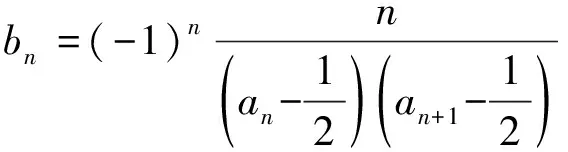
∴Tn=b1+b2+b3+…+bn