联系观点下的“两角差的余弦公式”教学

洪末凤

(安徽省太和县第一中学，安徽阜阳，236000)

“联系的观点”认为一切事物都处于相互联系之中,世界上根本没有不依赖于周围其他事物而孤立存在的事物.“联系的观点”指的是重视知识的比较和应用,形成全局的观点,形成和优化知识结构.注重“联系的观点”不仅是数学教育界的一个普遍趋势，而且更与“理解教学”具有直接的联系，因为所谓的“理解”就是指新学习的知识与主体已有的知识与经验建立起了直接的联系，因此“联系”的数目与强度直接决定了“理解”的程度.众所周知，“两角差的余弦公式”是“诱导公式”的推广，但是两个公式之间究竟存在怎样的联系，如何利用它们之间的联系开展教学是困扰广大一线教师的问题.下面，笔者就针对这节课，谈谈对此的看法.

1 关注知识的连续性，建立“为什么学”的联系

通常“两角差的余弦公式”都是通过“诱导公式”引入的.因为诱导公式反应了终边具有特殊对称关系角的三角函数的关系，由此联想到对于终边不具有对称关系的任意两个角之间是否也存在类似的关系，从而引出本节课的教学主题.这样的联系，看似是自然，实则学生很难想到.首先，“诱导公式”与“两角差的余弦公式”中间隔了“三角函数图像与性质”，这两部分的内容实际上是被认为的割裂开来，它们之间的联系也就变得不再那么紧密.根据联系的观点，越是相近的知识它们之间联系应该越强.基于这个观点，如果我们从“三角函数图像与性质”出发，能否建立起知识间的联系呢？

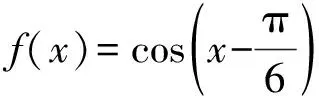
2 关注方法的迁移性，建立“如何学”的联系

一般数学公式的推导方法有很多，究竟选择哪种方法往往会让人纠结.在人教A版旧教材中，“两角差的余弦公式”就采用了两种方法，一个就是几何构造法，另一个就是向量法.两种方法虽然都能推导出公式，但都存在不足，最后都要对α,β的范围进行一般性的推广，而且几何法难以想到，向量法虽然简单，但跟三角函数似乎没多大关系.人教A版新教材中，采用的是旋转对称法，这种方法更加符合单元设计理念，符合学生的认知思维，但旋转对称法学，不容易想到，这就需要与诱导公式的推导方法建立起联系，然后通过类比迁移，从而获得公式的推导方法.

诱导公式的推导方法利用的是单位圆的特殊对称性，即“轴对称”与“中心对称”.在推导诱导公式时，是先已知对称性，然后再去确定角的终边，最后再寻找终边上坐标的等量关系.例如，事先已经知道两个角的终边关于y轴对称，具体做法是先确定角α的终边，再作角α终边关于y轴的对称终边，然后分析对称终边所指向角的大小，发现满足π-α；最后，有对称性，很容易发现这两个角所对应坐标之间的等量关系，从而获得关于π-α的诱导公式.

cos(α-β)的推导利用的是单位圆的旋转对称，它是比轴对称与中心对称更具一般性的对称，也就是说终边对称与轴对称都可以看成旋转对称，如果能够让学生明白这一点，公式推导也就迎刃而解.那么，如何建立起它们自己的联系呢？首先让学生思考，如果不事先知道对称性，能否确定α与π-α的终边？α终边事先可以规定，但对于π-α就不好确定，不过可以确定π-α的大小，如图1所示.根据研究三角函数关系一般准则，则需要把所有的角的始边都转移到x轴的正半轴上，如何把π-α的始边转移过去呢？自然想到的方法是“旋转”，从而就得到了比中心对称、轴对称更具一般性的对称，旋转对称.接下去，类比旋转对称的思路就可以确定α,β，α-β三个角的终边，再比较旋转前后图形的位置关系来寻找等量关系，最后获得cos(α-β)=cosαcosβ+sinαsinβ.

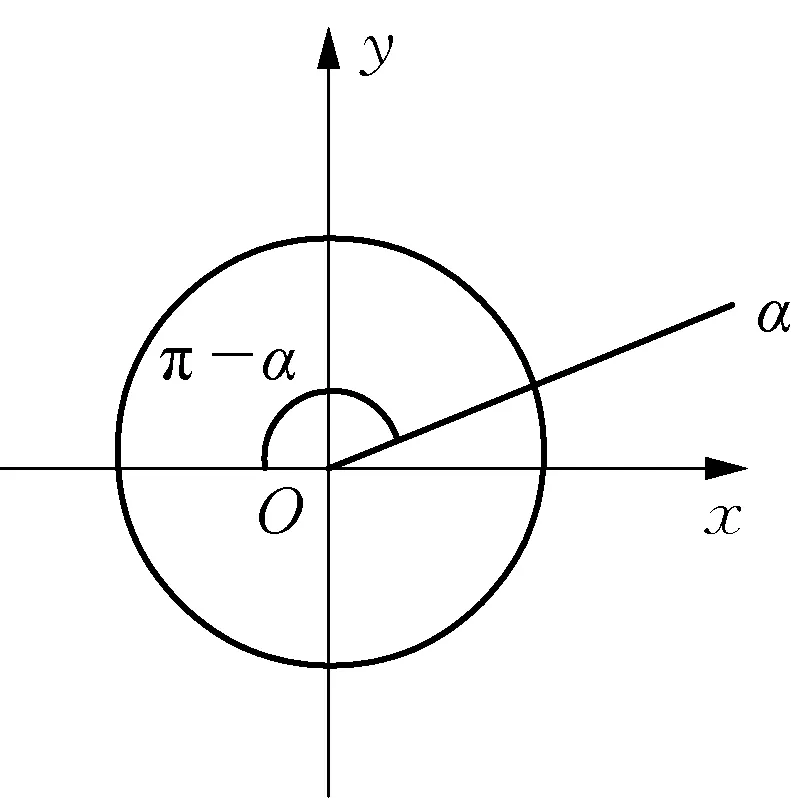
图1

3 关注思维的拓展性，建立更多的联系

数学教学的最终目标并不仅仅是让学生掌握知识与结论，更在于发展学生的数学思维.“两角差的余弦公式”也是如此，获得公式知识仅是其中一个目的，更应通过公式的发现、证明的过程建立起更多的联系，联系越多，就越容易形成结构化的数学思维体系.

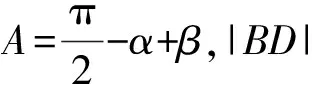
图2

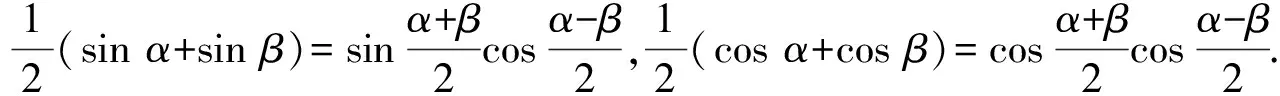
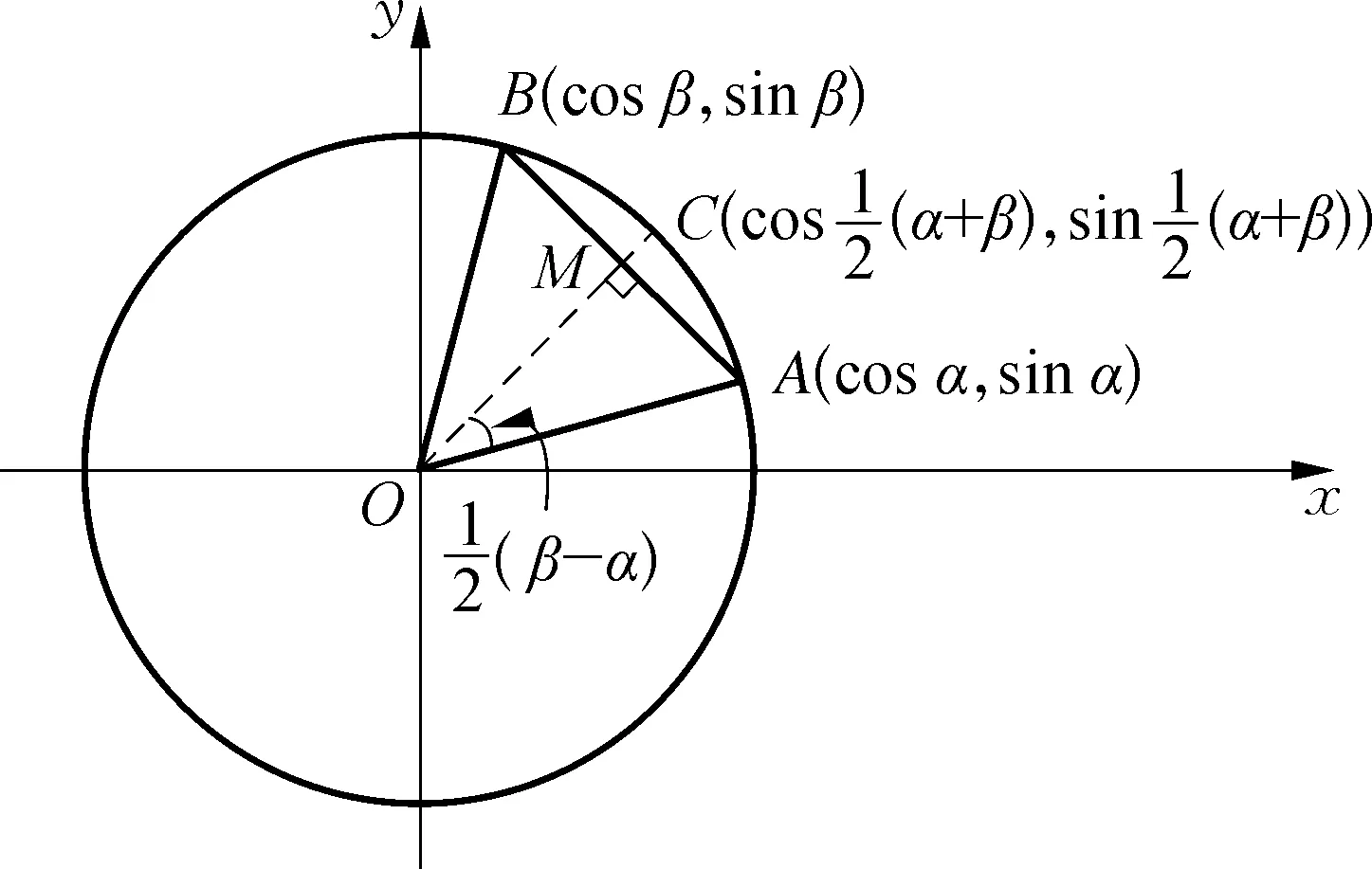
图3

最后，通过上述一系列公式的推导，充分凸显了单位圆作为研究三角函数的工具作用，也让学生进一步体会到三角函数是圆函数这一本质属性，从而通过圆把所有的三角函数知识都联系起来.

客观世界是一个普遍联系的整体，每一事物都不是孤立的存在，它和其他事物以各种方式相互依赖着，相互制约着，相互作用着.从数学的发展即可揭示出事物无不处于普遍联系之中.国际教育署与国际教育学会于2009年联合推出的指导性手册《有效数学教学》将“联系”列为数学教育最重要的“标准”之一，并且指出：当学生能够用相互联系的观点看待各种事物的时候，他们的学习生涯就开始了.