多思维视角切入，巧方法破解题目——一道最值题的探究

梁礼华

(福建省福州琅岐中学，福建福州，350017)

双变元代数式的最值(最大值或最小值)问题，一直是历年高考试题中一道亮丽的熟悉“面孔”.破解此类最值问题，常见的破解思维是借助基本不等式、函数或方程、三角函数以及导数等工具与思维切入，合理融合相关的数学知识，从数学知识、思维方法与能力等方面加以交汇与综合，恒等变形，巧妙处理，正确破解.

1 问题呈现

2 问题剖析

此题题目条件简单明了，通过两正实数所满足的二次方程关系，利用双变元之间的对应关系来确定其对应分式代数式的最值或最值范围问题.这里，题目条件关系式与结论关系式之间没有明显的过渡或联系.

解决此类问题的关键就是如何在已知条件的代数关系式背景下，通过认真审视试题条件，构建题目的条件与结论这两者关系式之间的“桥梁”，对相关的代数关系式进行合理的恒等变形，利用参数之间的关系转化与合理切入，巧妙处理.在不同的数学思维视角下，如基本不等式、函数或方程、三角函数以及导数等思维方式，进而确定不同的解题思维与对应的精彩解法.

3 问题解决

思维视角一：基本不等式思维

利用基本不等式来确定相关双变元代数式的最值问题，是解决此类问题中最常用的技巧与方法.解决问题的关键就是合理配凑条件与结论之间的关系，以及基本不等式成立的条件.利用基本不等式思维来处理问题时，有时可以直接利用，有时需要通过换元法、消元法等来综合与应用.

解析：

方法1：换元+基本不等式法

方法2：消元+基本不等式法

方法3：代“1”+基本不等式法

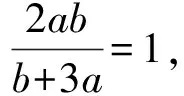
根据基本不等式，有(b+3a)2=(b+a+2a)2≥4(b+a)·2a，

评析：涉及双变元代数式的最值问题，最常见的思维方式就是借助基本不等式思维来处理.解决问题的关键在于通过对代数关系式的合理恒等变换，与结论对应的分式关系式加以联系，借助相应的技巧方法，或换元处理，或消元化简，或代“1”变换等，构建利用基本不等式的条件.

思维视角二：函数思维

利用一些特殊函数的图象与性质来确定相关双变元代数式的最值问题，是函数的图象与性质的进一步掌握与综合应用.解决问题的关键就是进行合理变形，转化为涉及其中一个参数的函数问题，利用特殊函数(如一次函数、二次函数等)的图象与性质来解决.特别的函数模型所对应的图象与性质是解决此类问题的基本数学模型.

方法4：二次函数法

评析：涉及双变元代数式的最值问题，函数思维是破解问题的一大基本技巧与策略.通过对代数关系式的合理恒等变换，或整体代入，或关系式转化，进行巧妙的合理消元，转化为涉及其中一个参数的一元二次函数问题，借助配方处理，利用二次函数的图象与性质等来确定对应的最值问题.

思维视角三：方程思维

利用方程来确定相关双变元代数式的最值问题，是初中方程与高中不等式求解的综合应用.解决问题的关键就是利用所求的结论关系式引入参数，构建涉及其中一个参数的方程(一般是一元二次方程)，利用方程有根的判别式法来构建不等式，通过不等式的求解来分析与解决.引入参数，待定系数法，综合不等式的求解是关键.

方法5：方程的判别式法

由于以上关于参数b的二次方程有正实数根，

评析：涉及双变元代数式的最值问题，方程思维也是破解问题的一大基本技巧与策略.通过对条件中的代数关系式的合理恒等变换，结合所求的代数关系式的设元处理引入参数，进而利用消元，转化为涉及其中一个参数的二次方程问题，利用二次方程有根的判别式法等来确定对应的最值问题.

思维视角四：导数思维

利用导数来确定相关双变元代数式的最值问题，是解决此类问题中最“万能”的一种技巧与方法.解决问题的关键就是合理消元，将所求的代数关系式转化为涉及其中一个参数的函数关系式，通过求导处理，结合函数的单调性来解决最值问题，往往运算量比较大，过程比较繁杂.

方法6：导数法

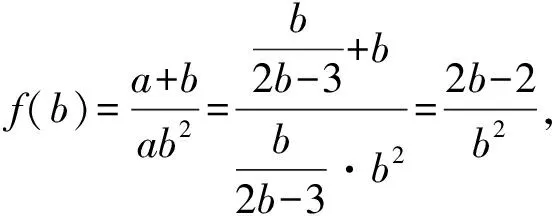
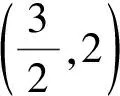
评析：涉及双变元代数式的最值问题，结合关系式的转化进行消元处理，将所求代数关系式转化为一元关系式，构建函数关系式，通过函数求导运算与转化，利用函数的单调性、极值以及最值等相关知识来确定对应代数式的最值或取值范围.

4 变式探究

探究1：根据条件改变所求解的代数关系式的形式，从另一个层面来求解对应代数式的最值问题，与原题在知识点考查、试题难度、思想方法应用等各个方面都比较相似.

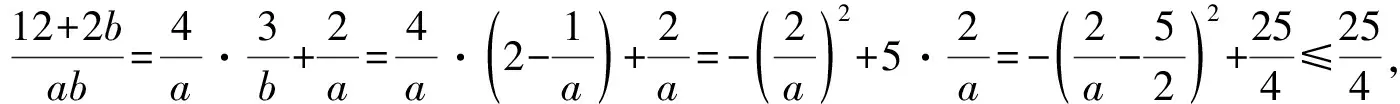
评析：根据条件中代数关系式的变形与转化，对所求解的代数关系式的变形进行消元处理，通过配方，利用二次函数的图象与性质来确定最值问题.当然，也可以参照原问题的解析的不同思维视角，尝试利用其他相关的方法来分析与解决，也可以达到解决问题的目的.

探究2：保留问题的条件背景，改变原来求解的分式代数式中的分子与分母的位置，得到以下对应的变式拓展问题.该变式问题考查的知识点与原题基本相当，但由于格式更加难变形，试题难度有所提升.

评析：利用所求分式关系式为正数的情况，与原来所求的代数式互为倒数，从而可以采用函数关系式的变形，结合二次函数的图象与性质来分析与解决.在原问题的基础上分析与解决，难度就比较大，可以尝试从其他思维方法来解决.

探究3：保留问题的创新情境，引入对应的参数来构建条件中的代数关系式，使得问题更具一般性，得到以下对应的变式拓展问题.该变式问题考查的知识点与原题基本相当，而试题难度有所提升.

根据基本不等式，有[b+(λ+1)a]2=(b+a+λa)2≥4(b+a)·λa，

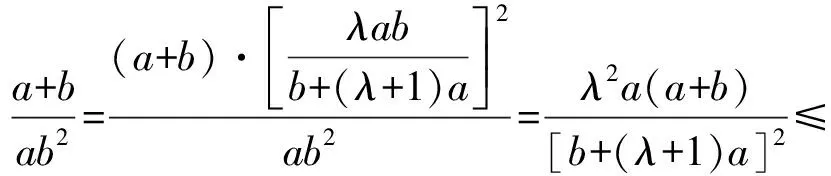
5 教学启示

5.1 总结技巧策略，形成思维习惯

此类涉及给定方程关系式的双变元或多变元的代数式最值或取值范围问题，命题新颖，背景变化多端，破解思维奇思妙想，破解策略多样，切入多变，方法精彩纷呈，殊途同归.具体解答时往往是结合题目条件给出的代数式(整式、分式、根式等)的基本特征(定和、定积、定比例等)，合理恒等变形与巧妙转化，正确数学运算与合理推理，借助一些相关的数学思想方法，综合一些常见技巧策略加以应用.

5.2 提升解题能力，形成学科素养

在解决一些相关的数学问题中，我们要不断积累、比较、总结、提升，总结技巧方法，归纳类型，总结并形成“多题一解”“多类一法”等，做到具体解题时有“法”可依，有“据”可查.巧妙融合与交汇相关的数学基础知识、思想方法等，学会应用思想方法等“武装”头脑，不断提升数学的解题技巧以及数学能力，举一反三，融会贯通，灵活变通，真正形成数学体系，提升数学能力，培养数学学科素养.