数列核心考点测试卷B 参考答案
一、选择题
1.A 2.C 3.D 4.B 5.D 6.C
7.A 8.B 9.B 10.A 11.C 12.C
二、填空题
13.64或1
15.
16.提示:在an+1两边同乘以2n+1,得2n+1·,则bn+1,解得,所以a=n
三、解答题
17.因为,所以=3an,所以an+1an=3an-3an+1。两边同除以得,所以,把以上这(n-1)个式子相加,得
18.(1)已知a1+2a2+3a3+…+n an=(n-1)Sn+2n(n∈N*)。
所以当n=1时,a1=2×1=2;
当n=2时,a1+2a2=(a1+a2)+4,所以a2=4;
当n=3时,a1+2a2+3a3=2(a1+a2+a3)+6,所以a3=8。

①-②得n an=(n-1)Sn-(n-2)Sn-1+2=n(Sn-Sn-1)-Sn+2Sn-1+2=n an-Sn+2Sn-1+2。
所以-Sn+2Sn-1+2=0,即Sn=2Sn-1+2,所以Sn+2=2(Sn-1+2)。
因为S1+2=4≠0,所以Sn-1+2≠0,所以
故{Sn+2}是以4为首项,2为公比的等比数列。
19.(1)方法一:因为an+1=2an+1,所以an+1+1=2(an+1)。
由a1=1知a1+1≠0,从而an+1≠0。所以数列{an+1}是等比数列。
方法二:由a1=1知a1+1≠0,从而an+1≠0。
(2)由(1)知{an+1}是以2为首项,2为公比的等比数列,所以an+1=2×2n-1=2n,即an=2n-1。
20.(1)因为方程a x2-3x+2=0的两根为x1=1,x2=b,所以解得a=1,b=2,所以an=2n-1。
(2)由(1)得bn=(2n-1)·2n。
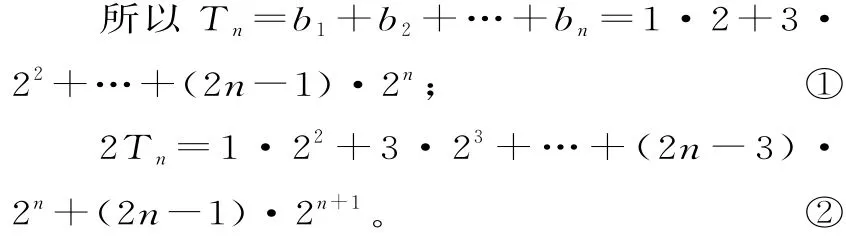
由②-①得Tn=-2(2+22+…+2n)+(2n-1)·2n+1+2=(2n-3)·2n+1+6。
21.(1)由Sn=2an-2,得Sn-1=2an-1-2(n≥2),两式相减得an=2an-2an-1,即又a1=2a1-2,所以a1=2,所以{an}是以2为首项,2为公比的等比数列,所以an=2n。
因为点P(bn,bn+1)在直线x-y+2=0上,所以bn-bn+1+2=0,即bn+1-bn=2,所以{bn}是等差数列。
因为b1=1,所以bn=2n-1。
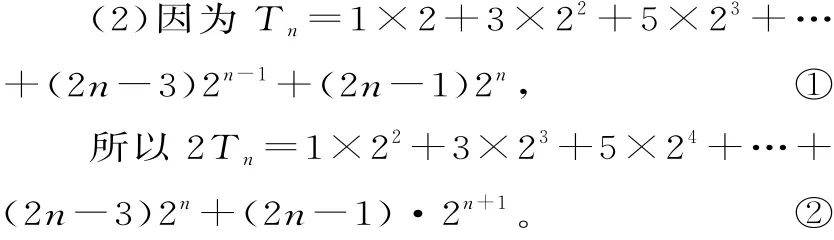
①-②得-Tn=1×2+2(22+23+…+
所以Tn=(2n-3)·2n+1+6。
22.(1)因为
由等比数列的通项公式知,若{an+1-是等比数列,则1-2p=0,即

