数列基础训练A 卷参考答案

一、选择题

1.B 2.B 3.A 4.C 5.A 6.A

7.C 8.B 9.C 10.B 11.B 12.C

二、填空题

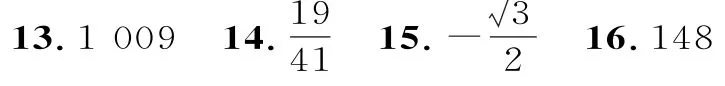
三、解答题

将n=1代入得a2=4a1。因为a1=1，所以a2=4。

将n=2代入得a3=3a2，所以a3=12。

从而b1=1，b2=2，b3=4。

(2){bn}是首项为1，公比为2的等比数列。理由如下:

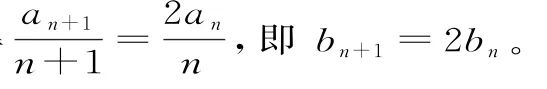
由条件可得又因为b1=1，所以{bn}是首项为1，公比为2的等比数列。

18.(1)设{an}的公比为q，由题设可得an=qn-1。

由a5=4a3得q4=4q2，解得q=0(舍去)，q=-2，q=2。

所以an=(-2)n-1或an=2n-1。

(2)若an=(-2)n-1，则由Sm=6 3得(-2)m=-18 8，此方程没有正整数解。

若an=2n-1，则Sn=2n-1。由Sm=6 3得2m=6 4，解得m=6。综上，m=6。19.

(1)因为an+1=an+6an-1(n≥2)，所

以an+1+2an=3an+6an-1=3(an+2an-1)(n≥2)。

因为a1=5，a2=5，所以a2+2a1=15，所以an+2an-1≠0(n≥2)。

所以数列{an+1+2an}是以15为首项，3为公比的等比数列。

(2)由(1)得an+1+2an=15×3n-1=5×3n，则an+1=-2an+5×3n。

所以an+1-3n+1=-2(an-3n)。

又因为a1-3=2，所以an-3n≠0。

所以{an-3n}是以2为首项，-2为公比的等比数列，所以an-3n=2×(-2)n-1，即an=3n+2×(-2)n-1。

20.(1)因为Sn+1=Sn+an+2，所以an+1-an=2，所以数列{an}是公差为2的等差数列。

因为a1，a2，a5成等比数列，所以a22=a1·a5，所以(a1+2)2=a1·(a1+8)，解得a1=1。

所以an=1+2(n-1)=2n-1。

(2)因为数列{bn}满足bn=(2n-1)·(2)1+(2n-1)=(2n-1)·2n。

所以数列{bn}的前n项和Tn=2+3×22+5×23+…+(2n-1)×2n。

所以2Tn=2×2+3×23+5×24+…+(2n-1)×2n+1。

所以Tn=6+(2n-3)×2n+1。

21.(1)当n=1时，a21+2a1=4S1+3=4a1+3，因为an＞0，所以a1=3。

当n≥2时，a2n+an-a2n-1-an-1=4Sn+3-4Sn-1-3=4an，即(an+an-1)(an-an-1)=2(an+an-1)，因为an＞0，所以an-an-1=2。

所以数列｛an｝是首项为3，公差为2的等差数列，所以an=2n+1。

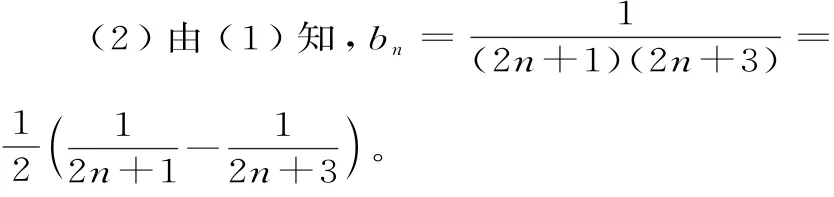
所以满足条件的最大正整数n为9 9。

预告：本刊下期与同学们一起探讨“空间几何、解析几何”的学习。