不等式强化训练B 卷参考答案

一、选择题

1.D 2.C 3.A 4.A 5.C 6.A

7.D 8.C 9.C 10.B 11.A 12.B

二、填空题

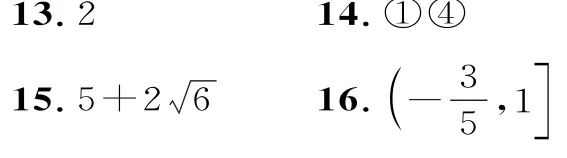
三、解答题

17.(1)当a=0或a=1时，解集为∅;

当a＜0或a＞1时，不等式的解集为｛x|a≤x＜a2｝;

当0＜a＜1时，不等式的解集为｛x|a2＜x≤a｝。

(2)当k＜1时，不等式的解集为｛x|k＜x＜1或x＞2｝;

当k=1时，不等式的解集为｛x | x＞2｝;

当1＜k＜2时，不等式的解集为｛x|1＜x＜k或x＞2｝;

当k=2时，不等式的解集为｛x|1＜x＜2或x＞2｝;

当k＞2时，不等式的解集为｛x|1＜x＜2或x＞k｝。

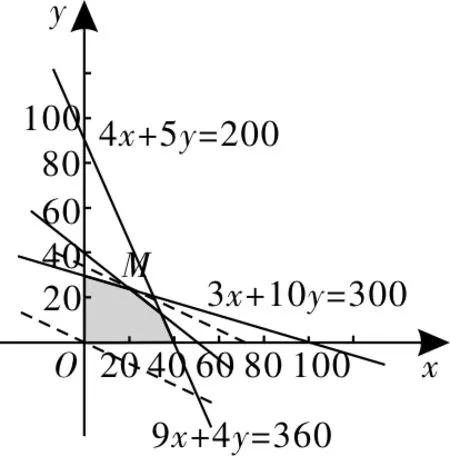
图1

在直线7x+12y=0向右上方平行移动的过程中，当经过点M(20，24)时z取最大值，所以该企业生产A，B两种产品分别为20t和24t时，才能获得最大利润。

19.设f(x)=x2+(m-1)x+1，x∈[0，2]。

若f(x)=0在区间[0，2]上有一个实数解，因为f(0)=1＞0，所以f(2)＜0或

若f(x)=0在区间[0，2]上有两个实数解，

综上，可知m≤-1。

20.(1)已知不等式组等价于:

从而得出点(x，y)所在的平面区域为图2中所示的阴影部分(含边界)。其中AB:y=2x-5;BC:x+y=4;C D:y=-2x+1;DA:x+y=1。

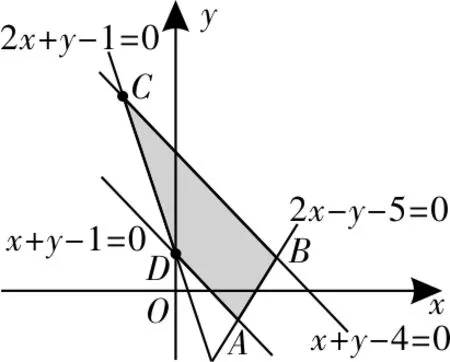
图2

(2)z表示直线l∶y-a x=z在y轴上的截距，且直线l与(1)中所求区域有公共点。

因为a＞-1，所以当直线l过顶点C时，z最大。

因为C点的坐标为(-3，7)，所以z的最大值为7+3a。

如果-1＜a≤2，那么当直线l过顶点A(2，-1)时，z最小，最小值为-1-2a。

如果a＞2，那么当直线l过顶点B(3，1)时，z最小，最小值为1-3a。

当且仅当n=13时等号成立。所以当建成13座球场时，每平方米的综合费用最省。

所以最多建26个网球场。

(2)设f(x)=a x2+b x+c(a≠0)。