全国名校等比数列测试题(A卷)答案与提示
一、选择题
1.A 2.B 3.C 4.A 5.C 6.C 7.C 8.A 9.B 10.C 11.D 12.B 13.B 14.A 15.C 16.D 17.C 18.C 19.B 20.D 21.A 22.B 23.C 24.C 25.C 26.A 27.B 28.B 29.C 30.A 31.A 32.C 33.C 34.B 35.B 36.B 37.D
二、填空题

三、解答题
57.因为{an}是等差数列,Sm-1=-2,Sm=0,所以am=Sm-Sm-1=2。
因为Sm+1=3,所以am+1=Sm+1-Sm=3。
故d=am+1-am=1。
59.因为Sn=2an+1,所以Sn+1=2an+1+1。
则an+1=Sn+1-Sn=(2an+1+1)-(2an+1)=2an+1-2an。
整理得an+1=2an。
又S1=2a1+1=a1,故a1=-1≠0。

61.由题意知q≠1。
由9S3=S6可得:
9(a1+a2+a3)=a1+a2+…+a6。
故8(a1+a2+a3)=a4+a5+a6=(a1+a2+a3)q3。等比数列。


62.(1)因为S1=a1=1,且数列{Sn}是以2为公比的等比数列,所以Sn=2n-1。
又当n≥2时,an=Sn-Sn-1=2n-1-2n-2=2n-2。
当n=1时,a1=1,不适合上式。

(2)a3,a5,…,a2n+1是以2为首项,4为公比的等比数列,故:
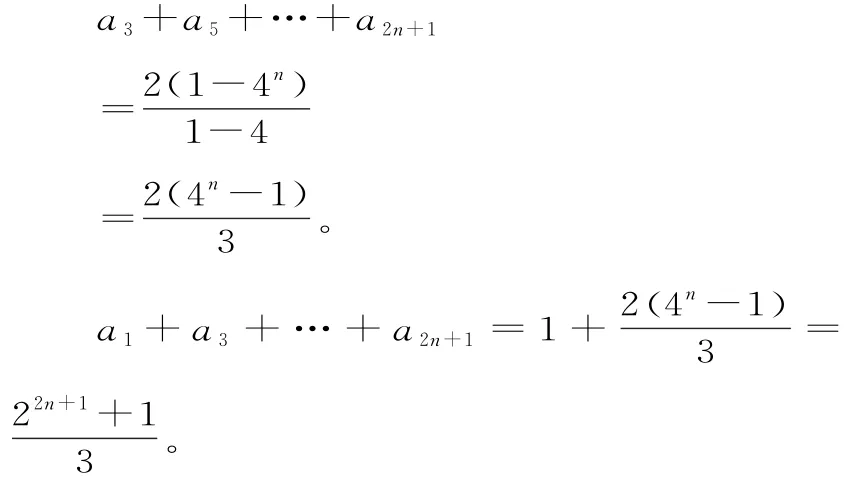
63.(1)当n=1时,S1=a(S1-a1+1),故a1=a。
当n≥2时,满足:
Sn=a(Sn-an+1);
Sn-1=a(Sn-1-an-1+1)。

若{bn}为等比数列,则有=b1b3。
而b1=2a2,b2=a3(2a+1),b3=a4(2a2+a+1),故[a3(2a+1)]2=2a2·a4(2a2+a+1),解得a=
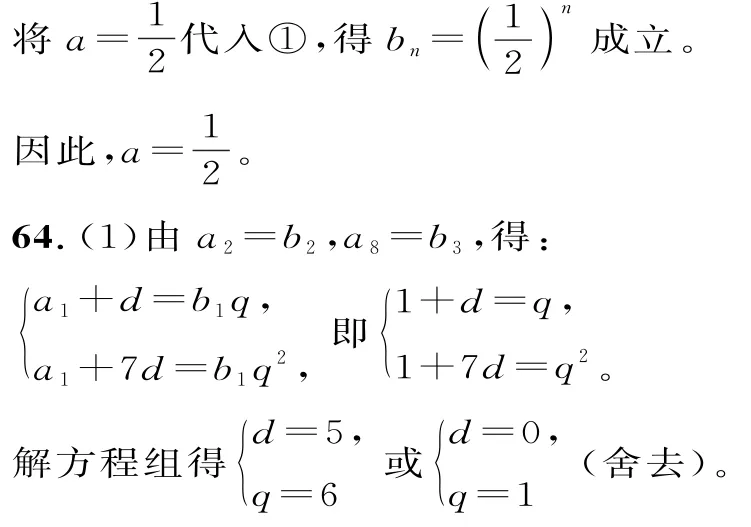
(2)由(1)知an=1+(n-1)·5=5n-4,bn=b1qn-1=6n-1。
由an=logabn+b,得:
5n-4=loga6n-1+b,即5n-4=nloga6+b-loga6。

65.(1)设等比数列{an}的公比为q。
因为S3+a3,S5+a5,S4+a4成等差数列,所以S5+a5-S3-a3=S4+a4-S5-a5。

当n为奇数时,Sn随n的增大而减小,所以

66.(1)设正数等比数列{an}的公比为q(q>0),由题意可得a1+a1q=6,a1+a1q+=30,解得a1=q=2(负值舍去)。
因此,an=a1qn-1=2n。
由bn·bn+1=an=2n,b1=1,可得b2=2。故有bn+1·bn+2=an+1=2n+1,对比可得2。
因此,数列{bn}中奇数项,偶数项均为公比为2的等比数列。


