浅谈等比数列中常见的错解剖析

■河南省驻马店平舆县第一高级中学高三八班 魏子龙

在等比数列学习中,我们有时会遇到一些似是而非的问题,此类问题往往是由于我们对某些概念或公式理解上的模糊认识,从而造成一些看起来正确而实际上错误的判断,使我们的解题思维走入误区。

误区一：对等比数列的概念理解不透彻,而造成的失误。

例1 若a,b,c是实数,则b2=ac是a,b,c成等比数列的（ ）条件。

A.充分不必要 B.必要不充分

C.充要条件 D.既不充分也不必要

因此,b2=ac是a,b,c成等比数列的充要条件。故选C项。

剖析：当a,b,c成等比数列时,b2=ac成立;由于a,b,c是实数,当b=c=0时,b2=ac虽成立,但b,c均为零,不可能是等比数列的项,即a,b,c不成等比数列。

故选B项。

误区二：忽视等比数列的公比不等于0的隐含条件而致错。

例2 已知数列{an}的前n项和为Sn=1+kan（k≠1）,判断数列{an}是否是等比数列。

错解：当n≥2时,an=Sn-Sn-1=1+kan-（1+kan-1）=kan-kan-1。

整理得kan-1=（k-1）an。

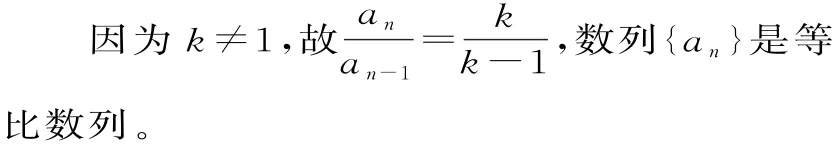
剖析：上述解法只适合k≠0的情形,因为等比数列中隐含条件q≠0,所以在解题过程中应考虑公比是否为0。

正解：

当n≥2时,an=Sn-Sn-1=1+kan-（1+kan-1）=kan-kan-1。

整理得kan-1=（k-1）an。

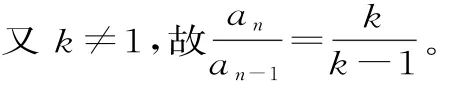
若k≠0,则数列{an}是等比数列;若k≠0,则Sn=1,数列{an}不是等比数列。

误区三：忽视了an=Sn-Sn-1成立的条件,从而导致错误。

例3 已知数列{an}的前n项和为Sn,满足log2（1+Sn）=n+1,求数列{an}的通项公式。

错解：因为log2（1+Sn）=n+1,所以1+Sn=2n+1,Sn=2n+1-1。

故an=Sn-Sn-1=（2n+1-1）-（2n-1）=2n,数列{an}的通项公式an=2n。

剖析：此解法忽视了起始项,即当n≥2时,an=Sn-Sn-1才成立。因此上面求出的通项公式an=2n只适用于n≥2的情况,上述结果是不完整的。

正解：因为log2（1+Sn）=n+1,所以1+Sn=2n+1,Sn=2n+1-1,Sn-1=2n-1。

当n≥2时,an=Sn-Sn-1=（2n+1-1）-（2n-1）=2n。

a1=S1=21+1-1=3≠21,不满足上式。

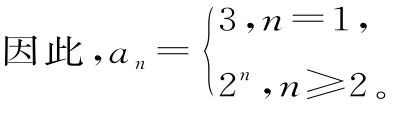
评注:公式an=Sn-Sn-1中隐含条件n≥2,所以当a1符合an（n≥2）的表达式时可合并一个通项公式;当a1不符合an（n≥2）的表达式时通项公式应分段表示。