全国名校数列测试题（B卷）答案与提示

一、选择题

1.D2.C3.B4.B5.C6.D7.A

8.D9.B10.C11.A12.D13.A14.A

15.D16.D17.D18.C19.B20.B21.C

22.B23.B24.C25.C26.C27.D28.A

29.C30.A31.C32.C33.C34.B

35.C36.B37.C38.D

二、填空题

三、解答题

59.(1)Sn为数列{an}的前n项和,已知a1=2,对任意n∈N*,都有：

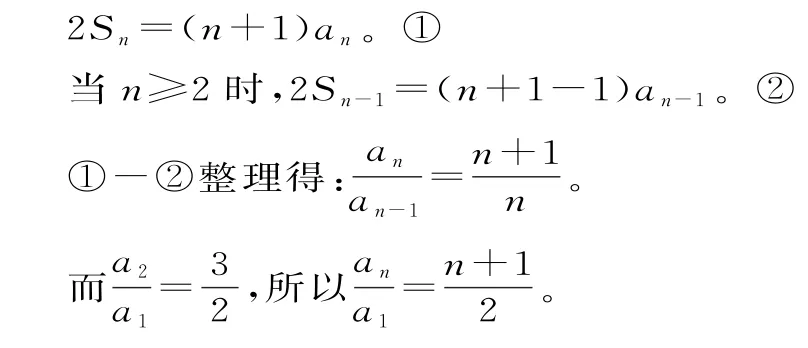
整理得an=n+1(首项a1=2符合通项公式),故an=n+1。

60.(1)由题意得故a2=3,a1+a3=10。则

解得q=3或q=(舍去)。

则an=a2qn-2=3n-1,

(2)设存在常数λ,使得数列{Sn+λ}是等比数列。

因为S1+λ=1+λ,S2+λ=4+λ,S3+λ=13+λ,所以(4+λ)2=(1+λ)·(13+λ),解得λ=。此时

所以存在常数λ=,使得数列是首项为,公比为3的等比数列。

61.(1)等差数列{an}满足a2=3,a5=9,则

所以an=a2+2(n-2)=2n-1。

数列{bn}满足b1=2,bn+1=abn,则：

所以数列{bn-1}是以2-1=1为首项,2为公比的等比数列,bn-1=1·2n-1=2n-1。

故bn=2n-1+1。

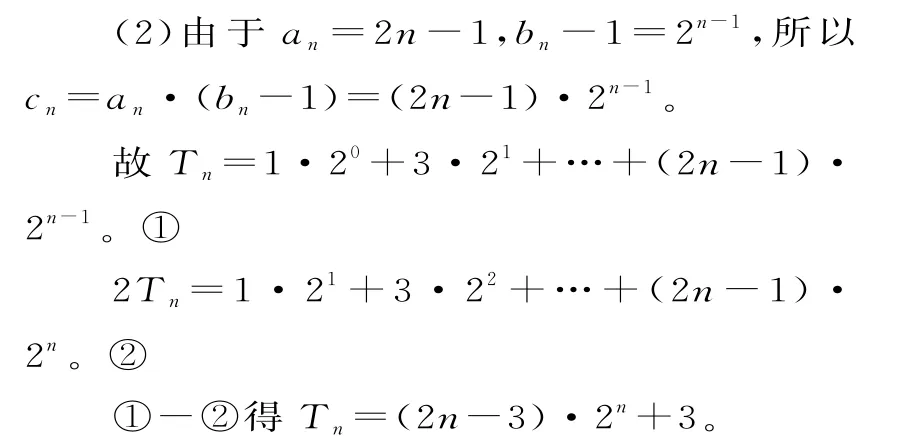
62.(1)设等差数列{an}的公差为d,前n项和为Sn,满足S3=12,且a1,a2,a4成等比数列。可得3a1+3d=12,即(a1+d)2=a1(a1+3d)。

解得a1=4,d=0或a1=d=2,则an=4,Sn=4n或an=2n,Sn=n2+n。

所以Tn=64n,或Tn=2·41+3·42+…+(n+1)·4n。

当Tn=2·41+3·42+…+(n+1)·4n时,4Tn=2·42+3·43+…+(n+1)·4n+1。

63.(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q。

已知a1=b1=1,,且a3=-10b2,也即1+d+q==-10q。

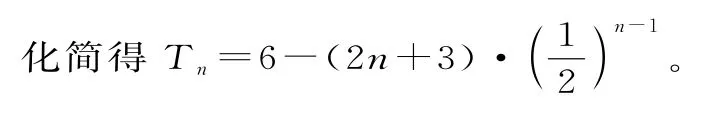
64.(1)由(Sn+1-Sn)(an+1-an)=,知an+1(an+1-an)=,即-an+1·an-=0。也即(an+1-2an)(an+1+an)=0。

因为数列{an}为正项数列,所以an+1=2an。数列{an}是以2为首项,2为公比的等比数列,则an=2n。

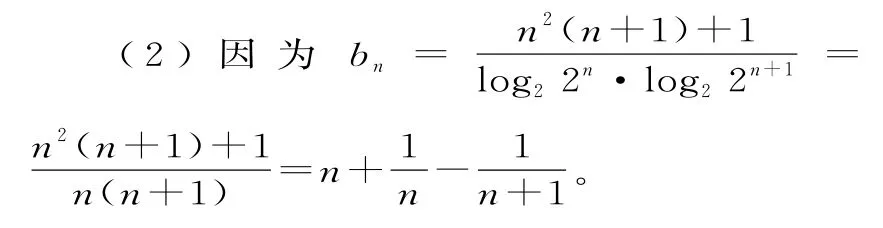
所以数列{bn}的前n项和：

65.(1)设等比数列{an}的公比为q(q＞0),由题意知

(2)由(1)得,bn=log3a2n-1=log332n-1=2n-1。

又bn+1-bn=2,故数列{bn}是首项为1,公差为2的等差数列。

数列{bn}是以2为首项,2为公差的等差数列,bn=2+(n-1)×2=2n,则

67.(1)由Sn=2an-2,得当n≥2 时,Sn-1=2an-1-2。两式相减,得an=2an-2an-1。当n≥2时,an=2an-1；当n=1时,S1=a1=2a1-2,a1=2。

则数列{an}是首项为2,公比为2的等比数列,an=2n。

由Tn+(n+m)an+1＜0,得2n+1-n×2n+1-2+n×2n+1+m×2n+1＜0 对任意n∈N*恒成立。

故m·2n+1＜2-2n+1,即对任意n∈N*恒成立。

68.(1)Sn=2an-2n-1。

当n=1 时,a1=S1=2a1-2-1,解 得a1=3；

当n≥2时,an=Sn-Sn-1=2an-2n-1-2an-1+2n-2+1=2an-2an-1-2,即an=2an-1+2,则an+2=2(an-1+2)。

故数列{an+2}是首项为5,公比为2的等比数列,an=5·2n-1-2。

数列{cn}是递减数列,数列{Tn}为递增数列。

则Tn的最小值为