多个公式 多条思路

■陕西省武功县教育局教研室 李 歆(特级教师)

等差数列是高考常考的知识点,通常都要利用通项公式与前n项和公式,按部就班列出方程求解,但有时在考场上这样做,既浪费时间,又效率不高。本文介绍等差数列通项与求和相关的两个有用的性质,希望能帮助同学们迅速地解题。

性质1设{an}为等差数列,an、am、ak分别为第n项、第m项和第k项,则有：

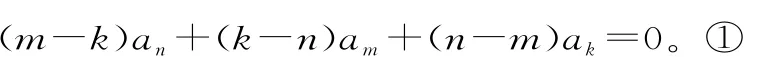
证明：设等差数列{an}的首项为a1,公差为d,则由等差数列的通项公式,得：

则(m-k)an+(k-n)am+(n-m)ak=(m-k+k-n+n-m)a1+[(m-k)(n-1)+(k-n)(m-1)+(n-m)(k-1)]d=0。

性质2设{an}为等差数列,Sn、Sm、Sk分别为前n项、前m项和前k项的和,则有：

证明：设等差数列{an}的首项为a1,公差为d,则由等差数列的前n项和公式得：

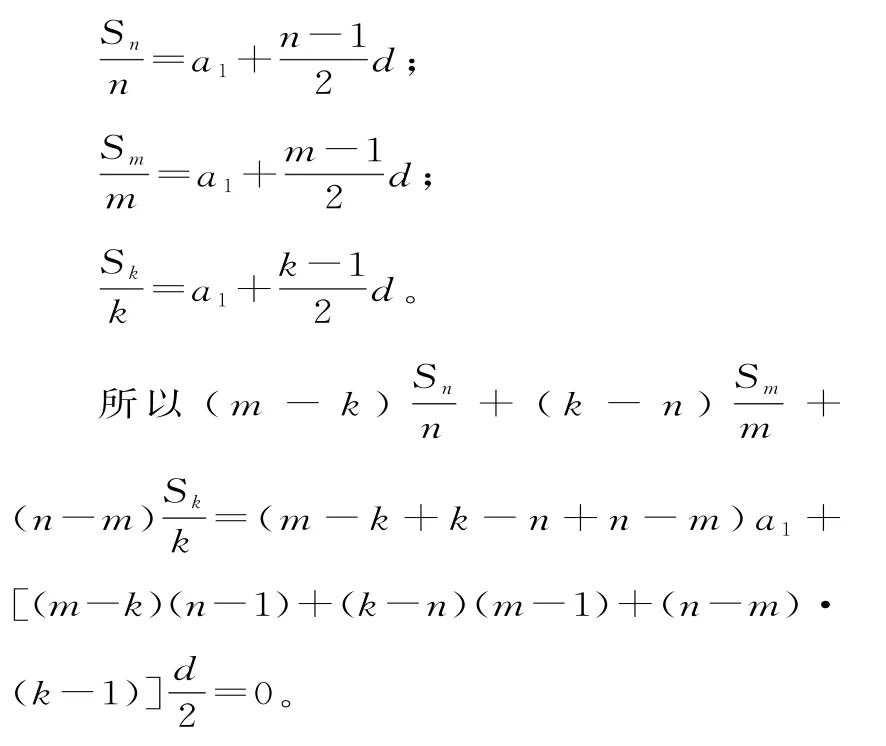
公式①与公式②结构简单、优美,在应用时注意通项与求和的下标按照n,m,k的顺序,而各项前面的系数依次为m,k,n中两项的循环差。

例1已知｛an｝是等差数列

解析：由公式①,得：(100-200)a50+(200-50)a100+(50-100)a200=0。

例2已知｛an｝是等差数列,am=n,an=m,则am+n=_____。

解析：由公式①,得：

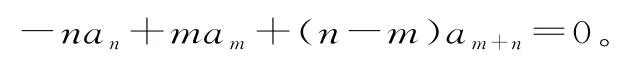
将已知条件代入,得-nm+mn+(n-m)am+n=0,解得am+n=0。

点评：一般地,对于等差数列｛an｝,由公式①,可得。如果an=n,am=m,m≠n,那么am+n=m+n。

例3已知｛an｝是各项非零的等差数列,则

解析：由公式①,得：

点评：这是一道新编题,如果按照常规方法,利用通项公式去处理,那么很容易“卡壳”,甚至出错。

例4已知等差数列｛an｝的前n项和为Sn,若S4=4,S6=12,则S20等于( )。

A.60 B.120 C.180 D.240

解析：由公式②,得。将已知条件代入,得,解得S20=180,故答案为C。

点评：按照通常的解法,先要两次利用前n项和公式建立两个方程,求出两个基本量a1和d,然后第三次再利用前n项和公式,才能求出结果,而用公式②却可一步到位。

例5等差数列｛an｝的前n项和为Sn,若a2=1,a3=3,则S4=( )。

A.6 B.8 C.10 D.12

解析：由公式②,得：

故答案为B。

点评：在公式②中,取k=n+m,则可得