正、余弦定理妙解三角形

■河南省平顶山市第一高级中学 刘邓辉

正、余弦定理将三角形的边和角有机地联系起来,从而使三角与几何产生联系,为求与三角形有关的量(如面积,其外接圆、内切圆的半径和面积等)提供了理论依据,也是判断三角形形状、证明三角形中有关等式的重要依据。

在利用正、余弦定理解三角形时,如果式子中含有角的余弦或边的二次式,要考虑用余弦定理；如果式子中含有角的正弦或边的一次式时,则考虑用正弦定理；以上特征都不明显时,则两个定理要珠联璧合,有可能都会用到。

一、求三角形的基本量

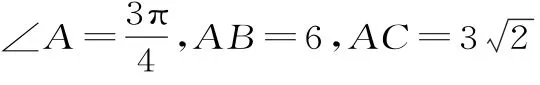
例1(2015·安徽卷)在△ABC中,,点D在BC边上,AD=BD,求AD的长。

解：设△ABC的内角∠BAC,B,C所对边的长分别是a,b,c。

由余弦定理得：

在△ABD中,因 为AD=BD,所 以∠ABD=∠BAD,所以∠ADB=π-2B。

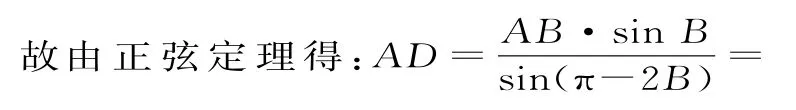
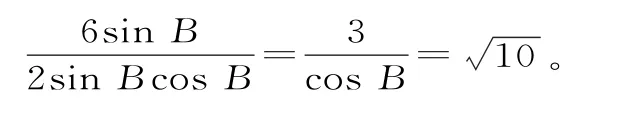
例2(2016·四川卷)在△ABC中,角A,B,C所对的边分别是a,b,c,且

(1)证明：sinAsinB=sinC；

(2)若b2+c2-a2=,求tanB。

解：(1)根据正弦定理,可设,则a=ksinA,b=ksinB,c=ksinC。

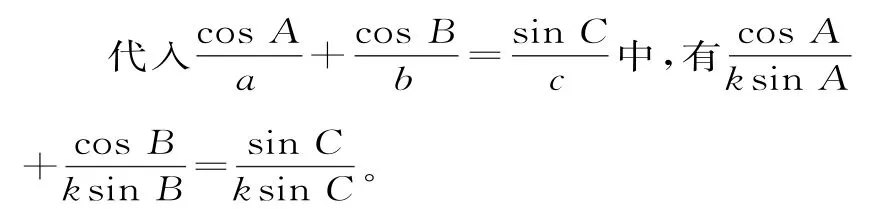
变形可得sinAsinB=sinAcosB+cosAsinB=sin(A+B)。

在△ABC中,根据A+B+C=π,有sin(A+B)=sin(π-C)=sinC。

所以sinAsinB=sinC。

点评：利用正、余弦定理解题是历年高考的热点,也是必考点,求解的关键是合理应用正、余弦定理实现边角的互化。其中正弦定理是一个连比等式,只要知道其比值或等量关系就可以运用正弦定理通过约分达到解决问题的目的。运用余弦定理时,要注意整体思想的运用。

二、解与三角形的面积有关的问题

例3△ABC中,角A,B,C的对边分别为a,b,c,若△ABC的面积S=(b+c)2-a2,则sinA=____。

例4在△ABC中,a,b,c分别为内角A,B,C的 对 边,且

(1)求A；

(2)若△ABC的面积,求sinC的值。

点评：正弦定理和余弦定理并不是孤立的,解题时要根据具体题目合理选用,有时还需要交替使用。应用时要注意化角法、化边法、面积法、初等几何法等方法的灵活运用,也要注意体会其中蕴含的函数与方程思想、等价转化思想及分类讨论思想。

三、正、余弦定理与三角问题的综合应用

例5已知函数

(1)若x∈,求函数f(x)的最大值和最小值,并写出相应的x的值；

(2)在△ABC中,角A,B,C的对边分别为a,b,c,满足且sinB=2sinA,求a,b的值。

因为sinB=2sinA,所以b=2a。

因为c2=a2+b2-2abcosC,所以