解三角形问题的三部曲

■河南省郑州市四中 李 亚

三角形是由三条边和三个角构成,反映三条边和三角关系的有正弦定理和余弦定理,因此,解三角形问题通常要完成下面三部曲：一找、二选、三转化。

一找：就是通过对已知条件和所求问题的观察,找出它们之间的差异,为解决问题指明入手的方向；

二选：就是根据已知条件和所求问题之间的差异,优先选准正弦定理或余弦定理,哪个先用与后用或者不用的问题,避免解题过程中走弯路；

三转化：就是将已知条件按照“边化角”或者“角化边”的方向转化,从而达到解决问题的目的。

下面以2019年高考试题为例,帮助同学们提高分析和解决三角形问题的能力。

例1(全国卷Ⅰ卷理科第17 题)△ABC的内角A,B,C的对边分别为a,b,c,设(sinB-sinC)2=sin2A-sinBsinC。

(1)求A的值；

分析：已知条件是角的关系式,第一问是求角,直接转化有困难,不妨按照常规思路,先用正弦定理进行“角化边”,之后再用余弦定理。第二问,增加了边的关系式,自然会想到“边化角”。

解：(1)由已知条件及正弦定理,得(bc)2=a2-bc,整理得b2+c2-a2=bc。

因为A为三角形内角,所以A=。

点评：已知条件和第一问虽然都只涉及角,但仅靠变形走捷径就会思维受阻。对第二问,参考答案先利用正弦定理得到,然后求出最后利用角的变形以及两角和的正弦公式获得了结果,这样解题技巧性较强。事实上,不少同学往往会得到cosC,接下来自然想到取平方后,用方程求解,但仍需要注意的取舍。

例2(全国卷Ⅰ卷文科第11 题)△ABC的内角A,B,C的对边分别为a,b,c,已知asinA-bsinB=4csinC,cosA==( )。

A.6 B.5 C.4 D.3

分析：已知条件给出了边和角的关系式,根据所求问题,先要用正弦定理进行“角化边”,最后再利用已知条件和余弦定理求解。

解：由已知条件及正弦定理,得a2-b2=4c2,则a2=b2+4c2。又由已知条件及余弦定理,得cosA=

点评：如果对已知条件进行“边化角”,那么就会得到sin2A-sin2B=4sin2C,接下来容易迷失解题方向。

例3(全国卷Ⅱ卷理科第15 题)△ABC的内角A,B,C的对边分别为a,b,c,若b=6,a=2c,B=,则△ABC的面积为_____。

分析：已知条件给出了一边、一角以及另两边之间的等量关系,需要用余弦定理求出另两边,最后再用边和角的面积公式求解。

解：由已知条件和余弦定理,得：

例4(全国卷Ⅱ卷文科第15 题)△ABC的内角A,B,C的对边分别为a,b,c,已知bsinA+acosB=0,则B=____。

分析：已知条件是边和角的关系式,题目要求角,自然要用正弦定理进行“边化角”。

解：由已知条件及正弦定理,得sinBsinA+sinAcosB=0。因为sinA≠0,所以sinB+cosB=0。又由已知条件易知cosB≠0,所以tanB=-1,B=

点评：如果由sinB+cosB=0 得,,那么由B=-B,同样可以求解。

例5(2019 年高考全国Ⅲ卷理科第18题)△ABC的内角A,B,C的对边分别为a,b,c,已知=bsinA。

(1)求B的值；

(2)若△ABC为锐角三角形,且c=1,求△ABC面积的取值范围。

分析：已知条件是边角关系式,第一问是求角,需要用正弦定理进行“边化角”。第二问给出了一条边,结合(1),可用边和角的面积公式,将问题转化为求某条边的取值范围。

解：(1)因为,所以由已知条件得

于是由正弦定理,得asinB=bsinA。

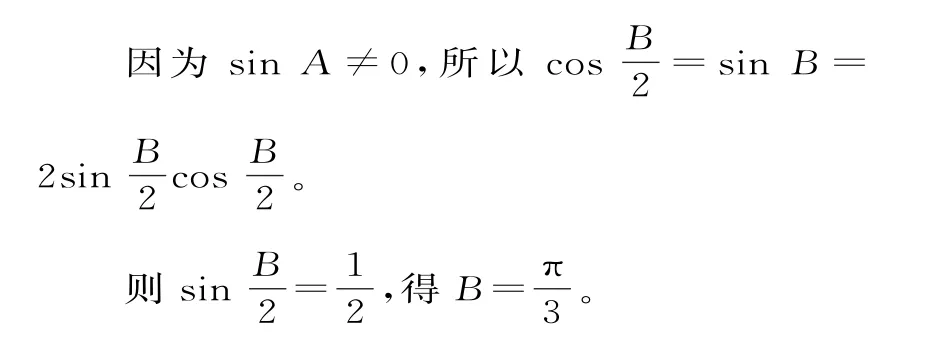
(2)根据已知条件并结合(1),则由面积公式,得：

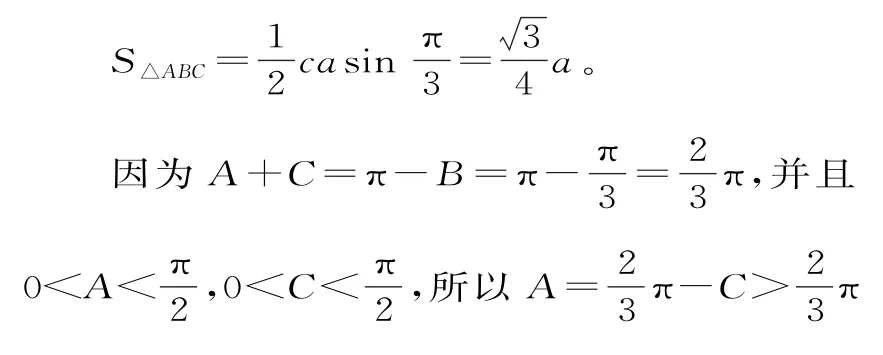
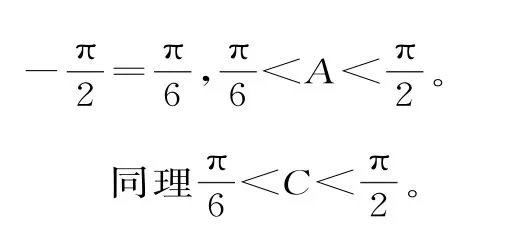
由正弦定理及正弦函数的单调性,得：

点评：对第二问,参考答案是利用正弦定理及三角公式,先得到,然后由角C的范围得到边a的范围,最后再进行求解,过程要复杂一些。此解利用正弦函数的单调性,直接得到边a的范围却要简便很多。

例6(北京卷理科第15题)在△ABC中,a=3,b-c=2,

(1)求b,c的值；

(2)求sin(B-C)的值。

分析：已知条件给出了一条边和另两条边差的值以及角B的余弦值,由此可知利用余弦定理可解第一问。对于第二问,根据两角差的正弦公式,必须求出角C的正弦值和余弦值,这又要用到余弦定理。

解：(1)由已知条件及余弦定理,得：

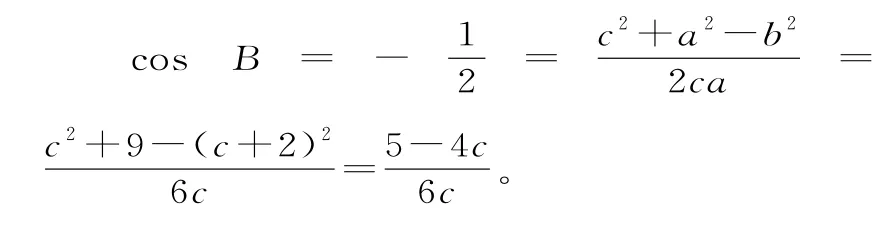
整理得c=5,由此得b=7。

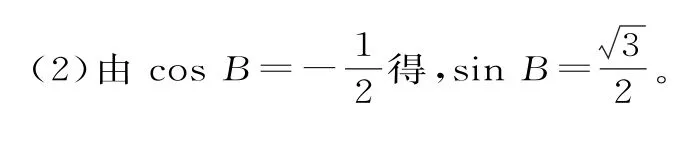
点评：此题将sin (B-C)变为sin (B+C),即为文科试题,虽然只是一个符号的改变,但求解却容易多了。由sin (B+C)=sinA及即可求解。

例7(浙江卷第14 题)在△ABC中,∠ABC=90°,AB=4,BC=3,点D在线段AC上,若∠BDC=45°,则BD=_____,cos ∠ABD=_____。

分析：依题意可求AC,由此可求sin ∠BCD,从而在△BCD中,由正弦定理可 求BD。又 因 为∠ABD+∠DBC=∠ABC=90°,所 以 cos∠ABD=sin ∠DBC,用三角公式可解。

解：由已知条件易知,AC=5。

点评：如果在△ABD中,用余弦定理求解cos ∠ABD,需要先求出AD,因AD=5-DC,则需要求出DC,又要用到正弦定理,这样做比较麻烦,而通过角的关系进行转化,则十分简便。